基于Lab色彩空间的自适应K-means图像分割方法

刘家丰，李东波

(南京理工大学机械工程学院，江苏 南京 210094)

图像分割[1]就是运用各种技术手段，将一幅图像分割成若干个具有感兴趣目标或独特性质的区域。图像分割是图像处理的基础和前提，是图像分析的关键步骤。图像分割方法有很多，根据其原理一般分为三大类[2-4]：1)阈值分割。即通过合适的阈值将图像分为背景和目标区域，具有运算速度快、计算简单的特点。2)区域分割。主要使用区域生长和分裂合并两种方法，常见的有种子法、四叉树分解法。3)边缘分割。它建立在边缘检测基础上，通过检测灰度级或者结构突变的地方来寻找边缘。随着各学科的发展和交叉，还出现了特定理论图像分割方法，这类方法都是基于某一具体的理论，如聚类分析、模糊集理论、基因编码等[5-6]。

K-means聚类方法[7-9]属于特定理论分割，其随机选择初始聚类中心，通过对初始聚类中心进行聚类运算来将像素分类。初始聚类中心数量和位置的选择，直接影响到后续聚类的结果。基于普通K-means的图像分割，其初始聚类中心往往是随机的，容易造成局部最优解，且数量需要手动设置，设置不当会导致过分割或欠分割，难以做到自适应分割。传统的基于灰度值K-means分割，对图像信息利用不够充分，聚类中心也往往不够合理，导致分割效果差强人意，所以需要一种能得到更好效果的图像分割方法。

1 Lab色彩空间

色彩是人类眼睛对于不同频率光线的不同感受，是客观存在而又可以被人们主观感知的。人类很早就认识到了色彩的存在，但是无法通过客观方式进行描述，后来人们建立了色彩模型，通过一维、二维、三维甚至四维空间坐标来表示某种色彩，将某种色彩分成不同坐标轴的多个值混合而成。在日常生活中广为人知的色彩模型为RGB模型[10]，也即三原色模型，它将红(red)、绿(green)、蓝(blue)三原色的色光以不同比例相加，以产生多种多样的色光。

Lab空间全名为CIELab色彩空间[11]，是在1931年国际照明委员会(CIE)制定的颜色度量国际标准基础上建立的，于1976年经修订命名为CIELab。Lab色彩空间不同于RGB色彩空间，其不受设备影响，与RGB色彩空间基于不同的设备拥有不一样的显示不同，它是一种基于生理特性的颜色系统，通过数字化方式描述人的视觉感应，适用范围广泛并常常作为一种标准化规范。

在Lab色彩空间中，一种色彩用L(亮度)，a(颜色)，b(颜色)3个参数描述。不同于RGB的用3种原色表示，Lab只有2种基础颜色，并且2种颜色属于混合色而不是单一原色。a取值范围为(+127～-128)，表示从红色到绿色；b取值范围为(+127～-128)，表示黄色到蓝色。在该颜色模型中，正值为暖色，负值为冷色，通过L(亮度)调整色调，取值范围为(0～100)，表示纯黑到纯白。

Lab色彩空间与其他色彩空间相比有以下优点：

1)在Lab色彩空间中明度和颜色是分开的，可单独调节。

2)色域宽阔。Lab属于标准化规范色彩空间，不仅包含了RGB、CMYK的所有色域，还能表现它们不能表现的色彩，只要是人肉眼能够感知的所有色彩，都可以通过Lab模型表现出来。

3)弥补了RGB和CMYK色彩空间色彩分布不均匀的不足。

Lab色彩空间表现能力较强，色域最宽，意味着在进行图像分割时可以使不同图像之间的差异更显著。同时，因为同样精度的Lab模型需要比RGB模型更多的数据信息，所以工业上RGB模型往往作为标准规范使用，获得的图像通常都是RGB图像，需要进行转换才能得到Lab色彩空间的图像。

RGB图像需要先转换成XYZ(CIE 1931 XYZ，几乎是所有颜色空间的基础)再转换为Lab，即RGB→XYZ→Lab，RGB转XYZ公式如下：

X=R×0.412 4+G×0.357 6+B×0.180 5

Y=R×0.212 6+G×0.715 2+B×0.072 2

Z=R×0.019 3+G×0.119 2+B×0.950 5

式中：X,Y,Z分别为XYZ色彩空间的三色通道的值。

XYZ再转换为Lab色彩空间：

L=116f(Y/Yn)-16

a=500[f(X/Xn)-f(Y/Yn)]

b=200[f(Y/Yn)-f(Z/Zn)]

式中：Xn、Yn、Zn分别为参照白点的CIE XYZ三色刺激值，计算时分别取96.422 1、100.000 0、82.522 1；f为以色道值与刺激值之比为变量的函数。f的取值情况如下：

式中：t为XYZ色彩空间色道值与刺激值之比。

图像转换到Lab色彩空间后，便由3个参数L，a，b所在色道组成，可进行后续操作。

2 基于Lab色彩空间的自适应K-means聚类方法

2.1 自适应K-means聚类方法

K-means聚类方法是1967年由MacQueen提出的，是典型的局域距离聚类算法。它首先确定K个类，每个类选取一个初始聚类中心。计算各对象到聚类中心的欧氏距离，并将对象划分到欧氏距离最短的一类，得到K个簇。一次迭代完成，计算新的聚类中心，一般情况下新的聚类中心可以取每个簇的平均值。多次迭代后，新的聚类中心与上次的聚类中心值相同或者两聚类中心之间的差值小于一个值，则认为算法已经收敛，聚类完成。

K-means应用到图像领域时，对于灰度图像，聚类中心通常是灰度值；对于彩色图像则变为多维，每个维度都是彩色图像的一个通道，例如对于RGB图像，其聚类中心是一个由R、G、B 3个色道组成的三维值。

算法流程如下：

1)从N个数据中随机选取K个作为聚类中心。

2)分别计算每个点xi(i=1,2,…,n)到K个聚类中心uj(j=1,2,…,k)的欧氏距离Di,j，找出每个点到这些聚类中心的欧氏距离最小值Di,p,Di,p=min(Di,1,Di,2,…,Di,p,…,Di,k)，则将点xi划分到p类。

4)判断收敛情况，将新聚类中心与旧聚类中心进行比较，若两者相差小于某阈值ε，则证明聚类完成，不小于则重复步骤1)～3)。

传统K-means聚类方法的初始聚类中心通常为随机选择，容易出现局部最优解。且聚类的数量K采用从某值开始的逐次递增选择最优值，工作量巨大。

因此，本文通过灰度直方图或各色道直方图，搜寻图像的波峰以获得像素的分布情况，从而确定初始聚类中心的位置和数量，被搜寻的波峰需要满足以下条件方可被搜寻到：

1)波峰必须呈现明显的突起。由于图像的复杂性，往往出现多个波峰，只能取有意义的波峰，如图1所示。

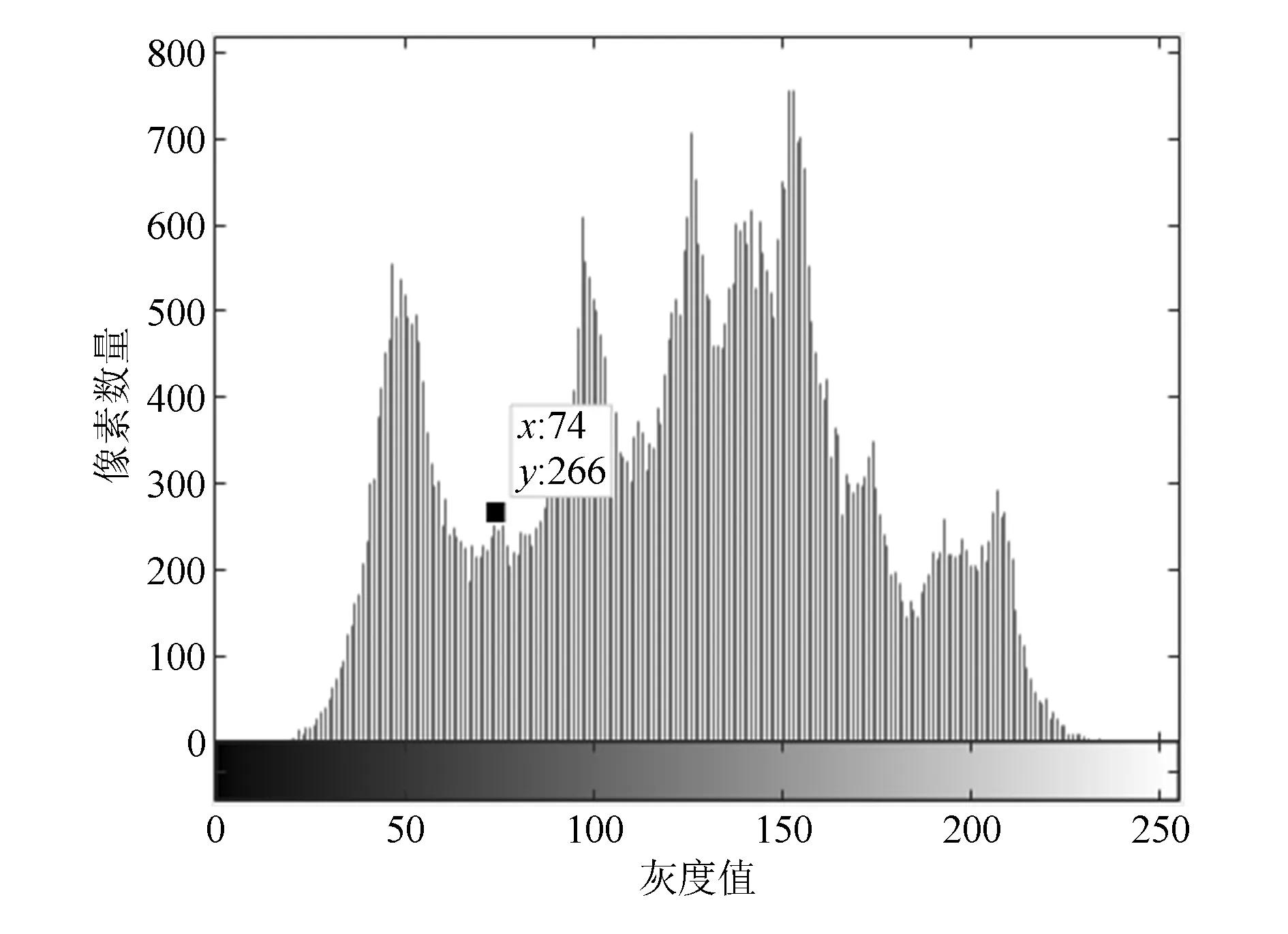
图1 多波峰情况

图中黑点部分是一个小波峰，明显可以看出，该波峰不属于像素点分布中心，其左右两个大波峰才属于像素集中心，因此必须有效剔除小波峰。

2)波峰不能是孤立值。图像上某一颜色均匀的小面积对象，在直方图中会体现为像素点集中在个别灰度级或通道值上，常表现为孤立的波峰。这个对象往往隶属于图像上一个大目标的一个部分，例如红色大衣上的一个黑色花纹，人脸上的黑色眼睛。这些目标虽然所占整体像素比例不高，但像素值均匀分布，容易在直方图上产生集中，在某一灰度级出现一个值极大的波峰，而这个波峰往往高出周围值较多。在实际图像分割时，如果对人物进行分割，当然希望眼睛和面容分割为一个整体，而不是单独分割成一部分；大衣上的黑色花纹，要与整个大衣归属于一类。如果每个小对象都被分割，会导致一张图像分割成数十个区域，造成过分割，孤立波峰情况如图2所示。

图2 孤立波峰情况

本文使用的波峰搜寻方法，以灰度图像为例，搜寻步骤如下：

1)从直方图X轴(0～255灰度值)某处(第一次为0)开始逐步搜寻，记录遇到的Y轴(每个灰度值像素分布数量)最大值Ym，随着搜寻不断替换，直至当前值小于上一个值。

2)由于当前值小于上一个值，则Ym仍为上一个值，继续搜索10个灰度级，若有6个灰度级Y轴值小于Ym，则认为Ym所在灰度值为波峰，记该灰度值为xi(i=1,2,…,k)。

3)沿X轴继续搜索剩余的灰度值，重复步骤1)和步骤2)，直至全部灰度值搜索完毕。

波峰搜寻完毕获得x1～xk共k个灰度值，即k个初始聚类中心。将波峰搜寻方法和K-means聚类方法结合，即得到自适应K-means聚类方法。

2.2 基于Lab色彩空间的K-means聚类分割

将Lab空间与自适应K-means聚类结合，得到新的图像分割方法。Lab色彩空间具有3个通道L，a，b，由于L通道为亮度通道，不能很好反映像素分布，只能采用a、b 2个通道进行二维K-means聚类。通过a、b双通道直方图计算聚类中心数量和初始位置时，会得到2个聚类中心数量k1和k2，分别表示基于图像2个通道像素的分布情况。

如果k1=k2，那么便可以得到k1，ui(i=1,2,…,k1)和k2，uj(j=1,2…,k2)2组值，则初始聚类中心为u(ui，uj)，即按照次序，依次将2个通道的聚类中心位置组合，得到聚类中心的二维坐标。

如果出现k1≠k2的情况，例如当k1小于k2时，这种情况下应当采用较小值，初始聚类中心为u(ui，uj)，(i=j=1,2,…,k1)。原因是选择小值，虽然代表图像少划分一类，但是如果需要，可以通过后续形态学操作或其他方法分割出来；采取大值，就可能产生过分割，将本属于同一类的像素分为2类，把图像目标分割到背景中，而从图像中被分割出去的信息，在后续步骤里无法补充。

本文算法流程：

1)彩色图像转到Lab色彩空间，分离出a、b 两个色彩通道，得到具有二维坐标的像素点xi(i=1,2,…,n)。

2)分别得到图像a、b通道的直方图并搜寻波峰，得到k=min(k1,k2)、ui、uj和图像的二维初始聚类中心u(ui，uj)，(i=j=1,2,…,k)。

3)将聚类中心带入K-means聚类算法，分别计算每个像素点xi(i=1,2,…,n)到各个聚类中心u(ui，uj)的最小欧氏距离，记作Dp(p=1,2,…,m,…k)，若Dm为最小距离，则分配xi到第m类。

5)判断收敛，即判断步骤3)和4)得到的新旧聚类中心之间差值是否小于阈值ε。本文取0.1，小于则聚类结束，否则转到步骤3)继续聚类。

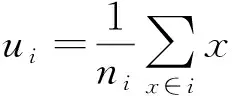
7)将得到的带有类别标识的mask用来把原图像分割成k个区域。

3 实验结果

为了验证本文提出的基于Lab色彩空间的K-means聚类分割方法，本文进行了大量的实验，分别使用基于灰度值的自适应K-means聚类分割和本文方法，对狗照片和人物图进行分割，分割结果如图3～图5所示。

图3 狗照片和人物图

图4 基于灰度值的自适应K-means方法分割结果

聚类中心数量和中心值见表1。

从图3～图5的对比可以明显看出，本文算法相较于传统的基于灰度值的自适应K-means算法能够更好地提取出目标，将目标与背景分离出来；与此同时，本算法在提取目标时，能够很好地保留目标边缘，保证目标轮廓的完整性。

图5 基于Lab空间的自适应K-means分割结果

表1 聚类中心位置与数量

图像分割结果的好坏仅用主观评价还不够，只有用量化标准才能更好地反映分割效果，本文使用GT(ground truth)图像计算分割图像的分割精度、过分割、欠分割等指标。

GT图像为含有理论分割结果的图像，是通过人工操作获得的精准理论分割图像；分割精度指正确分割像素与理论分割值的比例，越接近1证明精度越高；过分割率，指错误分割像素数量与理论值和错误分割值之和的比例，0为最优；欠分割率指未能正确分割像素数与理论值和错误分割值之和的比例，0为最优。表2、表3为两图分割结果各项指标参数。

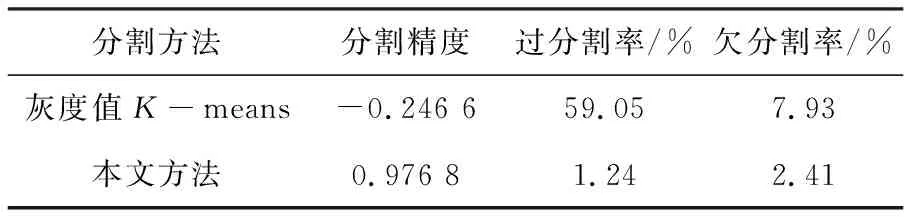
表2 狗照片分割评估

表3 人物图分割评估

实验证明,基于灰度值的自适应K-means算法虽然具有一定自适应能力，在一定程度上能够正确选择聚类中心数量和位置，但在面对部分图像时依然会产生分类不准确的情况，尤其在图像细节方面，会出现过分割和欠分割的现象。同时，在整体图像轮廓保留上，本文基于Lab色彩空间的K-means分割方法往往能更好地保留图像轮廓。以图4和图5的狗照片分割效果为例，本文方法几乎是沿着轮廓完整地将目标提取出来，边缘保留极好。

4 结束语

本文通过将图像转到Lab色彩空间，最大程度地增加了图像的像素差异，然后使用改进后的自适应K-means方法，在确定了聚类中心数量和初始位置后，对图像进行快速的聚类分割。实验结果证明，该方法自动给出的K-means聚类中心较为合理，能够较好地分割图像，尤其在保留图像边缘轮廓方面效果十分理想，可以最大程度保留图像信息，给后续图像处理提供更好的操作空间。