基于高超声速飞行器抗干扰故障诊断控制
2019-01-03叶杨飞徐露兵沈宝国孙小康
叶杨飞,徐露兵,沈宝国,孙小康
(1.江苏航空职业技术学院镇江市无人机应用创新重点实验室,江苏 镇江 212134)(2.扬州高等职业技术学校机电工程系,江苏 扬州 225000)
对高超声速飞行器的研究,其难点主要集中在它是一个复杂的多变量系统,具有强耦合和非线性特性[1-3]。干扰观测器起源于20世纪80年代,其抗干扰方法已较为成熟[4-6]。
高超声速飞行器在受到干扰和出现故障时怎样保证其动态系统的稳定性,引起了广大学者的关注[7-8]。目前对高超声速飞行器的研究取得了一定的成果。如文献[9]采用遗传算法设计模糊逻辑控制器,并将其应用在X-43A高超声速飞机的姿态控制中;文献[10]提出了一种基于模型预测控制和扩展线性化方法的高超声速飞行器跟踪控制策略;文献[11]提出了一种用自适应滑模干扰观测器来提高系统鲁棒性的方法,并将该方法应用到X-33飞行器的再入飞行中;文献[12]将终端滑模控制方法和RBF神经网络以及模糊干扰观测器相结合,并将其应用到空天飞行器的再入姿态飞行中。另外,在文献[13]~[15]中针对高超声速飞行器的故障问题,相关学者提出了一些新颖的解决方法,并达到预期的效果,但是这些方法通常针对线性化之后的模型,很难将其推广到阶次较高的非线性系统中。
本文基于高超声速飞行器纵向线性化之后的模型,在考虑外部干扰和故障的影响下,运用自适应投影算法以及设计干扰观测器,达到故障估计及对干扰补偿的效果。进一步,基于线性矩阵不等式,求解出相应的滤波器增益和观测器增益,结合Lyapunov函数分析方法,保证闭环系统在故障和干扰双重影响下系统的稳定特性。最后通过MATLAB/Simulink仿真验证了所提算法的有效性。
1 高超声速飞行器建模
1.1 高超声速飞行器纵向模型
高超声速飞行器是一个复杂的非线性系统。本文的研究以美国兰利实验室公开的锥形体(winged-cone)高超声速概念飞行器为例,其全状态非线性运动方程如下:
(1)
式中:h为飞行高度;r=r0+h,r0为地球半径;μ为引力常数;L为升力;D为空气阻力;T为推力;Iyy为沿y轴转动惯量;Myy为俯仰力矩;V为速度;m为质量;q为俯仰角变化率;α为攻角;γ为飞行航迹角。
1.2 高超声速飞行器纵向模型分析
高超声速飞行器初始模型为:

(2)
式中:x(t)=[Vγαhq]T∈R5,u(t)=[βδe]T∈R2;A,B,E为适维矩阵。
当有干扰以及故障存在时,式(2)可改写为:
(3)
式中:d(t),F(t),L1分别为未知干扰、故障以及适维矩阵。未知干扰d(t)由如下外延系统产生:

(4)
式中:W和N为已知的适维矩阵;ω(t)为外延系统状态。
1.3 高超声速飞行器系统状态滤波器以及干扰观测器设计
(5)

下文给出相关定义。
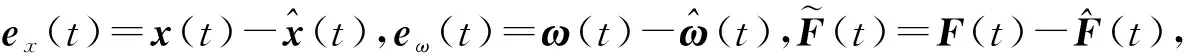
(6)
从而得到状态误差变化和干扰外延系统状态变化:
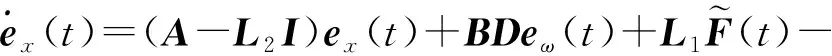
(7)
(8)
基于式(7)和式(8),可得如下增广模型:
(9)
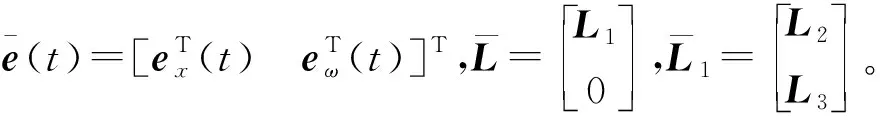


(10)
式中:C1,C2为已知的正常数矩阵。
1.4 相关定理证明
定理1:假设‖F(t)‖≤2/M,‖F(0)‖≤2/M。对于已知的参数k1,λ1,如果存在矩阵P>0,R满足如下线性矩阵不等式:
(11)

(12)
证明:构造如下Lyapunov函数
(13)
(14)

(15)

(16)
(17)

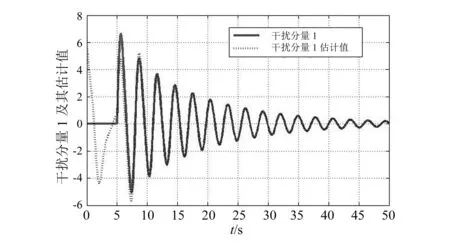
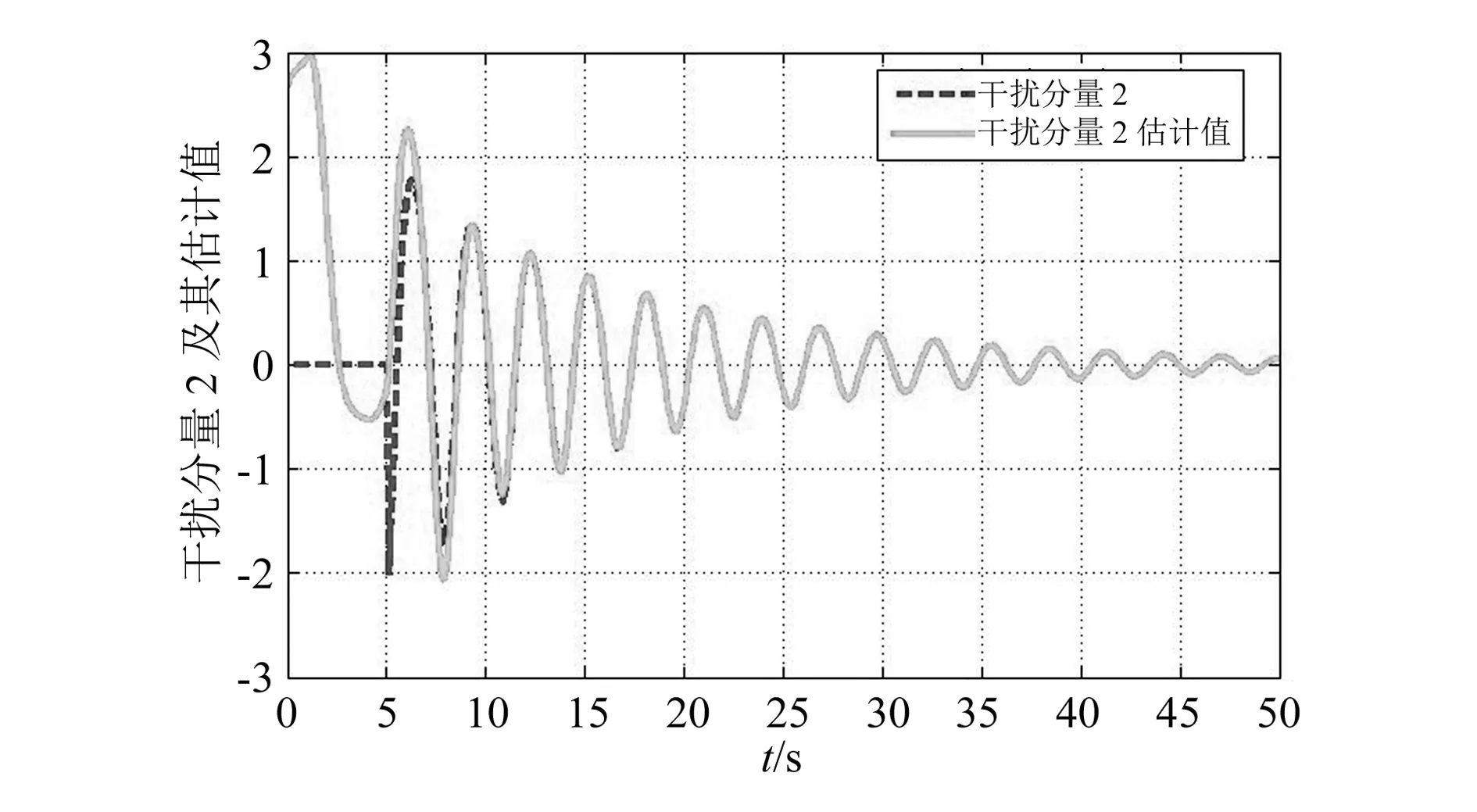
根据Schur补引理,令R=PL,可以得到线性矩阵不等式(11)⟺Ω (18) 假定飞行马赫数为15,平衡点为a0=1.79rad,V0=4 590.3m/s,h0=33 528m,γ0=0rad,q0=0rad/s,δe0=-0.38rad,βc0=0.21,α0=1.79rad,假定理想速度和高度值分别为Vd=4 640m/s、hd=33 628m,其他相关系统矩阵参数如下: 故障定义如下: 定义参数k1=0.6,λ1=1.5,C1=0.5,C2=2,通过MATLAB线性矩阵不等式工具箱求解线性矩阵不等式式(11),可得滤波器增益矩阵和观测器增益矩阵如下: L2=[0.000 14 0.005 20 -0.016 90 0.007 30 0.000 21]T L3=[0.003 26 0.006 28]T 结合MATLAB/Simulink仿真得到在干扰和故障双重影响下系统状态响应以及跟踪效果图。由图1和图2可知,在高超声速飞行器巡航阶段给出速度和高度指令信号(60,100)以及在干扰和故障双重作用下,其响应曲线大概在10s左右跟踪到其给定值。 由图3和图4说明,系统在遇到外来干扰时,通过设计相应的干扰观测器可以达到抗干扰的目的,系统在5s左右跟踪到相应曲线。 图1 速度及其跟踪效果图 图5显示在5s时系统发生故障,并在短时间内跟踪到故障值,说明投影算法能很好地对故障进行估计。 图2 高度及其跟踪效果图 图3 干扰分量1及其估计值 图4 干扰分量2及其估计值 本文基于高超声速飞行器模型,通过小扰动线性化得到其线性化方程。在干扰和故障双重作用下,通过设计干扰观测器以及自适应投影算法,基于线性矩阵不等式求解相应的滤波器增益和观测器增益,结合Lyapunov函数稳定性分析,进而保证闭环系统的强鲁棒性。通过MATLAB/Simulink仿真验证了所提算法的有效性。 图5 故障及其估计值
2 仿真算例






3 结束语

