基于谐波平衡法的储油罐幅频特性研究
2019-01-03穆雪恒穆慧杰康玉辉
穆雪恒,穆慧杰,康玉辉
(河南工学院机械工程系,河南 新乡 453000)
储油罐储存大量石油,一旦发生震动灾害,易造成石油泄漏或者火灾,将会造成巨大的生态环境的破坏和经济损失,因此提高储油罐的抗震性能有非常大的实际意义。大量学者对储油罐的自振特性、地震动力响应及屈曲破坏和减震抗震等进行了深入研究,并取得了丰硕的成果。文献[1]研究了大型浮顶储油罐的变形破坏机理,建立储油罐在爆炸载荷作用下的广义破坏屈服及失效破坏准则,用LS-DYNA软件对大型浮顶储油罐结构的罐壁动态力学响应进行了数值模拟;文献[2]将模型实验与数值模拟结果进行对比,研究了浮顶储油罐在可燃蒸汽云爆炸冲击作用下的变形过程和破坏机理;文献[3]建立了具有摆动效应的基础隔震储油罐的力学模型和考虑摆动效应的立式储油罐隔震体系的动力方程,并对基础隔震大型立式储油罐的地震响应问题进行了分析;文献[4]以某1×105m3钢制储油罐作为分析对象,对压力-位移的流固耦合模型建立等效动力扰动方程,并对储液罐在地震激励下的失稳概率进行了有效量化;文献[5]基于概率密度演化理论对带有环形隔板的圆柱形罐体中流体的晃动进行了研究;文献[6]对立式储油罐模型无隔震和有橡胶基底隔震的振动台的动态特性及地震响应进行了试验研究;文献[7]建立了立式储油罐的地震损伤模型,计算了常用的8种浮顶储油罐的损伤指数,并给出该指数范围,提出了基于损伤性能的立式储油罐抗震设计准则。目前,尚未有学者研究参数变化对储油罐动幅频响应的影响。
本文首先建立三质点体系隔震储油罐系统非线性动力学模型,推导出微分方程组,通过谐波平衡法将微分方程组转化为非线性方程组,利用数值分析软件MATLAB绘制幅频响应曲线,并分析参数对幅频响应曲线的影响规律。
1 动力学模型建立
1.1 动力学模型
柔性罐底周边隔震立式储油罐[8]新型抗震结构如图1所示,力学分析模型如图2所示。圆柱形薄壁基底四周安装有水平方向减震的耗能装置。为保证柔性基座在水平方向有一定的运动,将基底浮放于基础上,并使罐壁与基础之间保持一定间距。
1.2 量纲一化微分方程组
将地震动载荷简化为简谐波[9]
(1)

则隔震储油罐的动力学微分方程组为
(2)
式中:ks,kf,kx分别为液体晃动刚度、固液耦合刚度、附加减震装置刚度;cs,cf,cx分别为液体晃动阻尼、固液耦合阻尼、附加减震装置阻尼;ms,mf,mx分别为液体晃动质量、固液耦合质量和刚性脉冲质量;xs,xf,xx分别为晃动质量自由度、固液耦合质量自由度、刚性脉冲质量自由度。

图2 储油罐力学分析模型
为对方程组(2)解析解中幅值进行分析,引入特征频率ωi和阻尼系数ζi。
式中:i代表液体晃动s、固液耦合f、附加减震x等3种情况。
进一步定义τ=ωt,引入特征幅值Ac,则
量纲一化式(1),得到如下微分方程组
(3)
2 谐波平衡法求解
对于系统的一次谐波稳态响应,其近似表达式为
(4)

(5)
将式(5)与式(4)代入式(3),并令代入式(3)的后的方程等号两边cosτ项与sinτ项分别相等,得到如下形式方程组
(6)
式中:usc,uss分别为液体晃动s情况下阻尼幅值和液体晃动幅值;ufs,uxs分别为固液耦合f和附加减震x情况下液体晃动幅值。
通过谐波平衡法将微分方程组转化为线性方程组(式(6)),然后运用数值分析软件,通过对ω设定步长,逐个描点求解该非线性方程组,绘制幅频响应曲线。
3 频域动态特性
储油罐参数见表1,以50 000m3立式浮顶储油罐为研究对象,简谐波作为地震动输入波,最大值为0.1g。幅频响应曲线如图3所示。
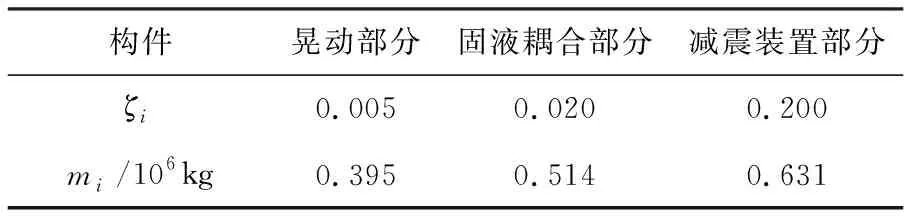
表1 储油罐参数值
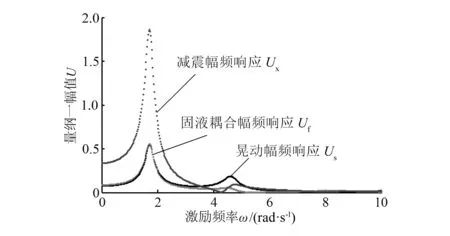
图3 幅频响应曲线
由图可知,随着激励频率发生变化,系统各个部分的幅频响应曲线变化规律不同。频率对减震部分的幅频响应曲线影响较大。当ω=1.7rad/s时,Ux达到最大值;ω>1.7rad/s时,各部分幅频响应幅值除在ω=4.5rad/s左右发生较小波动外,其余区间内幅值均随ω增加而减小。
4 阻尼系数对幅频响应的影响
参数分析过程中如果未作说明,均按照表1取值。阻尼系数ζf=0.010时,ζx变化对幅频响应Uf的影响如图4所示。

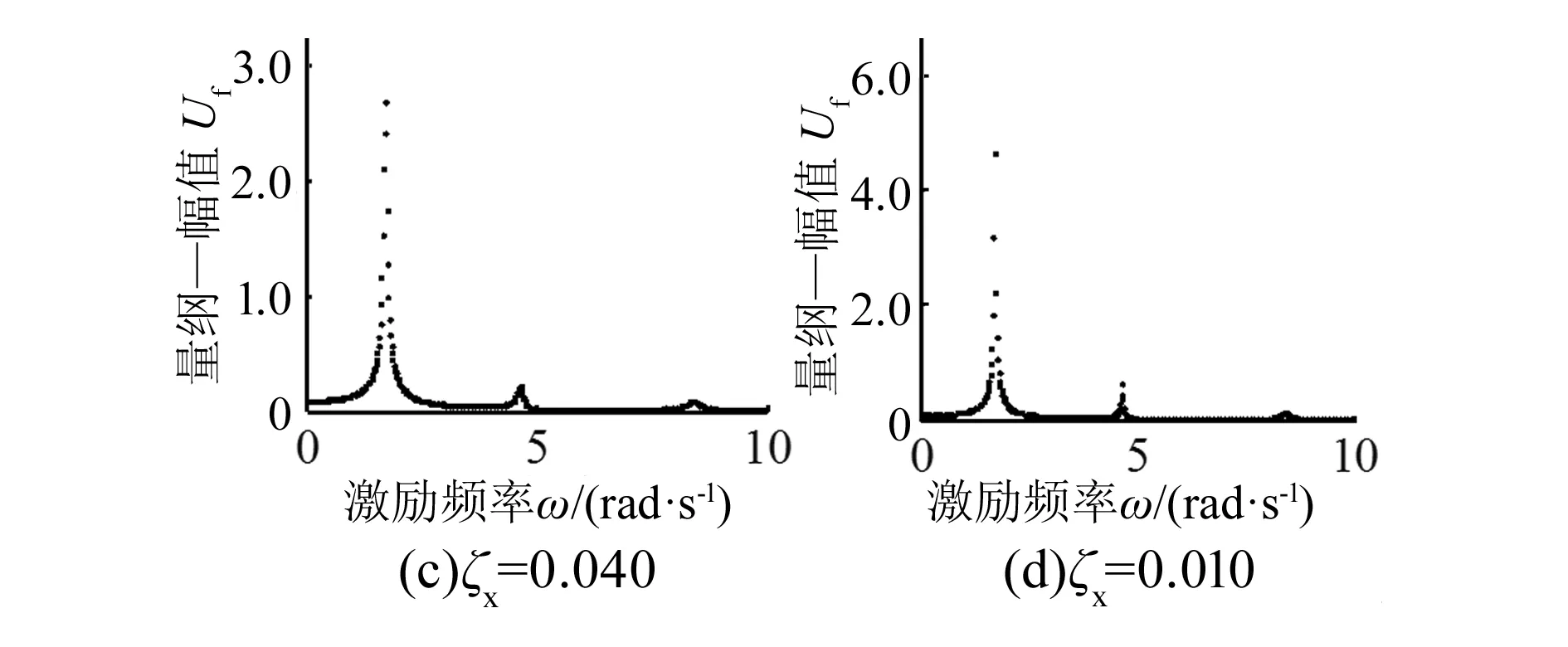
图4 ζx对幅频响应Uf的影响
阻尼系数ζx=0.100时,ζf对幅频响应Uf的影响如图5所示。

图5 ζf对幅频响应Uf的影响
阻尼系数ζx=0.100、ζf=0.010时,ζs对幅频响应Ux的影响如图6所示。

图6 ζs对幅频响应Uf的影响
由图4、图5和图6对比可知,阻尼系数变化只对幅值产生影响,对固有频率值不产生影响,Uf最大值均出现在第一阶固有频率处。ζs增大时,Uf发生微小变化;ζf增大时,第三阶固有频率处幅值增大;ζx增大时,各阶固有频率值处幅值均变大。
5 结论
本文通过建立三质点体系模拟柔性基底储罐体系力学分析模型,推导微分方程组,运用谐波平衡法分析系统动态特性,得到如下结论:
1)建立隔震储油罐的动力学微分方程组,量纲一化微分方程组,利用一次谐波平衡法建立非线性方程组,通过数值分析软件MATLAB可以绘制系统幅频特性曲线。
2)激励频率增大时,系统各部分幅频响应幅值均不同。ω=1.7rad/s时各部分幅频响应幅值均出现最大值;ω>1.7rad/s时系统幅频响应幅值整体呈下降趋势。
3)阻尼系数变化时,ζx对Uf影响最大,ζx越小激发得到的各阶固有频率处幅频响应幅值Uf越大,对储油罐造成的破坏越大。阻尼系数ζx变大有助于降低幅频响应幅值,提高储油罐的抗震性能。
