粘性平面液膜喷入可压缩气流中的线性稳定性分析*

曹建明，熊 玮，李雯霖，张叶娟

（1.长安大学汽车学院，西安 710064；2.中国第一汽车集团公司技术中心，长春 130011）

0 前 言

喷嘴喷射出的平面液体层称为平面液膜射流，被广泛应用于固定式燃气轮机、航空航天飞行器等内燃式动力机械的燃烧室中。对液膜射流碎裂雾化过程的研究一直受到国际流体与燃烧学界的普遍关注，是当今研究的热门课题[1]。20世纪50年代，SQUIRE[2]、HAGERTY等[3]最先研究了介于不可压缩稳定气体介质中的非粘性平面液膜射流的不稳定性。LIN[4]、MANSOUR[5]、HASHIMOTO[6]、LI[7-9]、曹建明[10-14]、杜青等[15-17]应用线性稳定性理论对液膜射流的不稳定性和碎裂机理进行了大量的理论和试验研究工作。LIN应用线性稳定性理论研究了粘性平面液膜进入不可压缩气流中的时空模式。LI的主要贡献在于考虑了液体粘性的影响，并应用线性稳定性理论分析了液膜两侧不同气流速度下的射流碎裂。LI首先提出了在液膜射流两侧气流流速不等时，表面波形呈现近正对称波形（para-varicose）——上下气液交界面的相位差角α→和近反对称波形（para-sinuous）——α→0的概念，从而将射流表面波的相位差扩展到全方位的0 ≤α≤，使整个线性稳定性理论变得有序而连贯。曹建明将环境气体的可压缩性引入了线性稳定性模型中，为高速空气助力环境下液膜射流的不稳定性分析和碎裂过程研究做出了贡献。杜青等人研究了加热条件下液膜射流的行为和特征。然而，上述研究得到的各种条件下的色散关系式均是有量纲形式的。根据相似理论，量纲一关系式要比有量纲形式的关系式包含更多的信息量，适用范围更广，具有更大的优越性。本文在上述研究的基础上，通过对控制方程组、以及运动学和动力学边界条件的线性化和量纲一化，得到了量纲一化的色散准则关系式，据此可以研究气液流速比之差d、韦伯数We、欧拉数Eu、雷诺数Re、马赫数Ma等量纲一参数对液膜射流碎裂过程的影响。推导得到的色散准则关系式是一个复数指数方程，表面波增长率随表面波数的变化关系是隐含的。由于色散准则关系式的复杂性，无法得到其解析解，只能应用穆勒方法[18]得到色散准则关系式的数值解，绘制曲线图进行分析。

1 模型的建立

图1所示为一个二维平面液膜射流表面波的简图。液膜的厚度为2a，a为平面液膜喷嘴出口的半厚度（m）。沿基流射流方向设定为x轴，沿液膜厚度方向设定为y轴。液膜射流以喷射压力Pl=Pl（Pl,0 ） = c onst（.MPa）、密度ρl= c onst（.kg/m3）、x方向速度Ul=Ul（Ul, 0 ） = c onst.（m/s）、y方向速度为vl= 0（m/s），喷射进入背压为Pg=Pg（Pg,0 ） =const.（MPa）、密度ρgj≠ c onst.（kg/m3）、x方向速度Ugj=Ugj（Ugj, 0 ） = c onst.（m/s）、y方向速度为Vgj=0（m/s）的气体环境中。其中：脚标“j= 1”表示上气液交界面参数，“j= 2”表示下气液交界面参数。α是上下气液交界面表面波的相位差角。

图1 平面液膜表面波Fig.1 Surface wave of plane liquid film

经扰动后附加的压力、x方向速度和y方向速度的扰动值分别为pk=pk（x,y,t），uk=uk（x,y,t），vk=vk（x,y,t）。则有量纲形式的合流参数为：pk-tot（x,y,t） =Pk+pk（x,y,t），uk-tot（x,y,t） =Uk+uk（x,y,t），vk-tot（x,y,t） =vk（x,y,t）。其中：脚标“k= l”表示液相参数，“k= g”表示气相参数，“tot”表示基流量与扰动量相加的合流参数。

2 纳维-斯托克斯控制方程组

纳维-斯托克斯控制方程组的一般形式为：连续性方程

动量方程

式中：t为时间；ν为运动学粘度系数；div为散度，等于哈密顿算子的点积，即为拉普拉斯算子。由于实际的喷雾应用的弗劳德数（Froude number,Fr）非常大，因此质量力Fbxl可以忽略不计，即Fbxl= 0 。考虑液相为不可压缩粘性流体，液体密度液体运动学粘度系数气相为可压缩非粘性流体，气体密度气体运动学粘度系数液相和气相的纳维-斯托克斯控制方程组可以分别写为：

连续性方程

动量方程

对连续性方程和动量方程进行量纲一化和线性化后，可得液相和气相的纳维-斯托克斯控制方程组的展开形式。

连续性方程

x-动量方程

y-动量方程

3 色散准则关系式

根据量纲一化和线性化的纳维-斯托克斯控制方程组，建立液相和气相微分方程。由于液相为不可压缩流体，可以引入流函数进行推导。液相微分方程为

气相微分方程为

求解液相和气相微分方程，以得到通解和特解，需要引入运动学边界条件和附加边界条件。运动学边界条件为

由于气体的粘度系数比液体的小得多，气液交界自由面上的切应力近似为零，有附加边界条件

求得微分方程的通解和特解后，可以得到扰动压力。液相扰动压力为

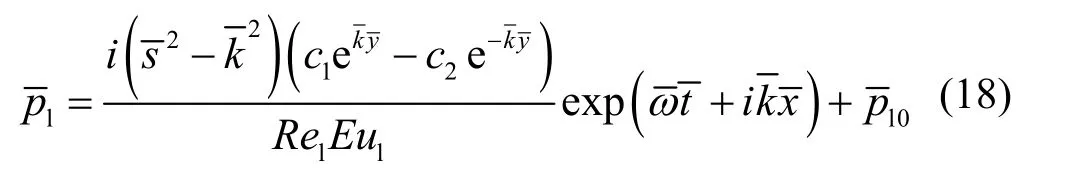
式中：积分常数

在上气液交界面处，气相扰动压力为

在下气液交界面处，气相扰动压力为

液相和气相扰动压力求出后，代入动力学边界条件。

上气液交界面动力学边界条件

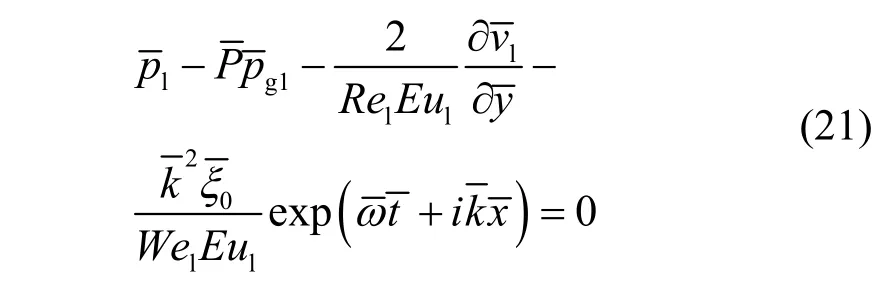
下气液交界面动力学边界条件

根据动力学边界条件可推导出气液交界面相位差角及量纲一形式的色散准则关系式（norm dispersion relations）。气液交界面相位差角可由下式确定：

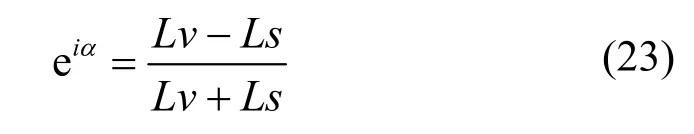
当α=0时，eiα=1，为反对称波形（sinuous）；当α=π时，eiα=-1，为正对称波形（varicose）；当α→0时，eiα→1，为近反对称波形（para-sinuous）；当α→ π时，eiα→- 1，为近正对称波形（para- varicose）。

近反对称波形色散准则关系式

近正对称波形色散准则关系式

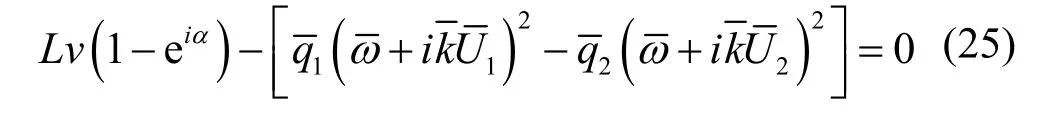
合并式色散关系式

推导得到的量纲一形式的色散准则关系式非常复杂，无法得到其解析解。因此需要编制 Fortran语言程序，采用穆勒方法[18]进行数值计算，求取色散准则关系式的数值解。

4 数值计算结果及其分析

4.1 液膜两侧气液流速比之差的影响

图2所示为粘性平面液膜喷射进入大气状况气体介质中的情况，在不同的液膜两侧气液流速比之差下，表面波增长率随表面波数的变化规律。其中，图2a所示为近反对称波形，图2b所示为近正对称波形。从图中可以看出，随着从0增大到1，表面波增长率和支配表面波增长率减小；从1再增大，表面波增长率和支配表面波增长率持续增大。表明液膜两侧刚有气流速度差时，表面波波长变长，液膜稳定，小的气流速度差不利于液体的碎裂；随着速度差进一步加大，表面波波长变短，并促使液膜碎裂。比较图2a和图2b可知，在一定的情况下，近反对称波形的表面波增长率比近正对称波形的表面波增长率大近乎一个数量级，这表明近反对称波形的表面波比近正对称波形的更不稳定，因此，近反对称波形的表面波将在液膜的碎裂过程中起主导作用。

图2 气液流速比之差对表面波增长率的影响：（a）近反对称波形，（b）近正对称波形Fig.2 Effect of ratio difference between gas and liquid on wave growth rate: (a) para-sinuous wave; (b) para-varicose wave

4.2 液流韦伯数和雷诺数的共同影响

图3所示为液流韦伯数和雷诺数对表面波增长率的影响。其中，实线所示为近反对称波形，虚线所示为近正对称波形。从图中可以看出，随着液流韦伯数Wel和雷诺数Rel的增大，表面波增长率增大，而且支配表面波增长率支配波数都增大，说明液流韦伯数和雷诺数是液体的不稳定因素。比较实线和虚线曲线可以看出，在液流韦伯数和雷诺数一定的情况下，近反对称波形的表面波增长率比近正对称波形的表面波增长率大一倍左右，这表明近反对称波形的表面波比近正对称波形的更不稳定。

图3 液流韦伯数和雷诺数对表面波增长率的共同影响（实线表示近反对称波形，虚线表示近正对称波形）Fig.3 Effect of liquid Weber number and Reynolds number on wave growth rate (real line denotes para-sinuous wave, dashed line denotes para-varicose wave)

4.3 液流欧拉数的影响

图4 液流欧拉数对表面波增长率的影响（近反对称波形）Fig.4 Effect of liquid Euler number on wave growth rate( para-sinuous wave)

图4所示为平面液膜近反对称波形表面波增长率随欧拉数的变化关系。可以看出，随着液流欧拉数Eul的增大，表面波增长率增大，而且支配表面波增长率支配波数都增大，说明液流欧拉数也是液体的不稳定因素。

4.4 气流马赫数的影响

当气流马赫数Magl＜ 0 .3时，气体的压缩性可以忽略不计，为不可压缩流体；当气流马赫数Magl≥0.3时，就必须要考虑气体的可压缩性对液膜碎裂的影响，为可压缩流体。图5所示为大气状况不同的气流马赫数下，表面波增长率随表面波数的变化规律。

图5 大气状况下气流马赫数对表面波增长率的影响：（a）近反对称波形；（b）近正对称波形Fig.5 Effect of gaseous Mach number on wave growth rate under atmosphere status: (a) para-sinuous wave; (b) para-varicose wave

图5a为近反对称波形，图5b为近正对称波形。可以看出，不论哪种波形，表面波增长率总是随着气流马赫数的增大而增大。比较两种波形，近反对称波形的表面波增长率总是比近正对称波形的大。这表明在相同的流动条件下，近反对称比近正对称更加不稳定。同时还可以看出，随着气流马赫数从0增大到0.7，近反对称波形的表面波增长率增大的幅度逐渐缩小，而近正对称波形的表面波增长率增大的幅度逐渐扩大。显然，气流马赫数提高了液膜的不稳定度，并且使不稳定波向短波区移动，这表明气体的可压缩性将加速液膜的碎裂。

图6为高气体密度下气流马赫数对表面波增长率的影响。与图 5a比较，高气体密度下随着气流马赫数的增大，表面波增长率增大的幅度在逐渐扩大。说明在高气体密度下，高马赫数对液膜的不稳定性影响更大。

图6 高气体密度下气流马赫数对表面波增长率的影响（近反对称波形）Fig.6 Effect of gaseous Mach number on wave growth rate under higher gas density (para-sinuous wave)

4.5 液流韦伯数、雷诺数和气流马赫数对支配表面波增长率和支配波数的影响

显然，不论哪种扰动波形及液体粘度如何，支配表面波增长率和支配波数总是随着液流韦伯数、雷诺数和气流马赫数的增大而增大，尽管在小马赫数下（Ma≤ 0.3），增长量非常小。说明在较大的液体喷射速度和较大的环境气体空气动力作用下，液膜更容易碎裂。同时也可以清楚地看到，在任何气流马赫数下，近反对称波形的支配表面波增长率总是比相应的近正对称波形的大，而近反对称波形的支配波数总是比相应的近正对称波形的小。

图7 液流韦伯数、雷诺数和气流马赫数的共同影响：（a）对支配表面波增长率的共同影响，（b）对支配波数的影响（实线表示近反对称波形，虚线表示近正对称波形）Fig.7 Effect of liquid Weber number, Reynolds number and gaseous Mach number: (a) effect on dominate wave growth rate;(b) effect on dominate wave number (real line denotes parasinuous wave, dashed line denotes para-varicose wave)

5 结 论

根据纳维-斯托克斯控制方程组建立了粘性平面液膜射流喷射进入可压缩气流环境中的模型，对液、气相控制方程组进行了量纲一化和线性化，引入流动运动学和动力学边界条件，推导得到了色散准则关系式。采用穆勒方法编制 Fortran语言程序，进行数值计算，求取色散准则关系式的数值解，并进行液膜射流的稳定性分析。结果表明：表面波增长率随着量纲一参数-液膜两侧气液流速比之差液流韦伯数Wel、液流雷诺数Rel、液流欧拉数Eul、气流马赫数Mag的增大而增大；支配表面波增长率和支配波数随着液流韦伯数Wel、液流雷诺数Rel和气流马赫数Mag的增大而增大，液膜射流变得更加不稳定。在相同的流动条件下，近反对称波形的表面波增长率和支配表面波增长率总是比近正对称波形的大，说明近反对称波形的表面波更加不稳定，并在液膜射流的碎裂过程中起支配作用。