翻转课堂教学模式下高三数学复习课探究——以《解三角形》复习教学为例

赵 芯

(福建师范大学第二附属中学，福建 福州 350015)

高三数学复习课，面广、量大、时间紧，既要回顾知识点、大量的习题，又不能忽视学生的思维过程，很难兼顾。翻转课堂可以提供一种有效的解决途径。作为信息化时代背景下的新型教学模式，翻转课堂重新调整学生的学习过程，学生在课前利用微视频、学习任务单等完成“信息传递”的知识学习，课堂内通过师生互动交流、同伴协作探究完成知识的“吸收内化”。以高三数学复习课《解三角形》为例，利用现代信息技术，提高课前预习的有效性，提升课堂学习的参与性，注重课后复习的巩固性，同时优化教学过程，使教师从“知识传授者”变为“学习指导者”，学生从“被动接受者”变为“主动研究者”[1]。

1 翻转课堂新理念

翻转课堂，即Flipped Classroom或Inverted Classroom，也称颠倒课堂，是指重新调整课堂内外的时间，将学习的决定权从教师转移至学生[2]。翻转课堂教学借助信息技术，让学生在课前自主学习传统课堂中教师面对面教授的知识内容，在课堂上通过“生生”“师生”的交流协作完成传统课中和课后的实践、反思等活动。这种教学模式尊重学生的个性需求，注重学生的个性化发展，改变了传统教学中的师生定位，建构了新的学习流程——先学后教、以学定教，即课前，学生利用微视频、学习任务单，结合教材自主学习，找出疑难困惑点，实现知识传递； 课中，教师、学生通过交流互动、协作探究、答疑解惑等完成知识内化； 课后，学生主动对所学知识进行归纳、总结、梳理，形成自己的知识体系[1]。

2 高三数学复习课教学设计

翻转课堂教学模式重新架构了课堂内外的学习过程，重组了课堂教学结构，改变了知识传授和知识内化的顺序，发挥了学生的主观能动性，体现了一切为了学生的思想[3]。《普通高中数学课程标准(2017年版)》要求在《解三角形》的复习教学中，学生通过对任意三角形中边角关系的探究，熟练掌握正弦定理、余弦定理及其简单应用，并能运用相关知识解决一些与测量、几何计算有关的实际问题[4]17-18。该节课公式多，变换灵活，技巧性强，传统的“接受式”复习模式，即复习概念、公式，精讲例题，以教师讲解为主，学生自主复习、主动探究意识不强。翻转课堂教学模式，以学生为中心，在自主先学、交流助学、以用促学、课后共学等教学流程中，引导学生主动建构新知识，完成课前自学、课中内化、课后升华的知识探究过程[3]。

2.1 教材解读与学情分析

2.1.1 教材分析

《解三角形》是初中《解直角三角形》内容的延伸，是三角系列的最后一章，凸显了基础性、工具性、应用性。重在研究三角形中边、角之间的数量关系，从实际问题中构建数学模型，将实际测量、航海等问题转化为可解的三角形问题，逐渐提高学生运用数学知识分析和解决实际问题的能力[4]17-18。

2.1.2 学情分析

该节课的授课对象为福建师范大学第二附属中学理科宏志班高三(10)班的学生。学生数学基础较好，理科思维能力强，学习积极性高，具备自主学习和协作交流的意识，能熟练使用QQ，微信等网上工具进行学习、交流。

2.2 主要环节与设计意图

2.2.1 微课视频，自主先学

作为翻转课堂教学的重要开端，课前，学生观看有关微视频，自主先学，并完成课前学习任务单，实现知识传递。教师通过学生的反馈，及时、准确了解学生的掌握情况，了解学生学习的“盲点区”“困惑区”，进行合理的教学设计，帮助学生掌握知识。微视频及课前学习任务单主要内容包括： 1) 正弦定理、余弦定理的内容及证明； 2) 利用正弦定理可以解决哪两类有关三角形的问题； 3) 利用余弦定理可以解决哪两类有关三角形的问题； 4) 三角形面积公式； 5) 基础练习。

练习1△ABC中，a，b，c分别是角A,B,C的对边。

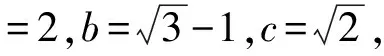
2) 若b=8，A=60°，c=3，则ɑ=________。

3) 若A=45°，C=30°，c=10，则ɑ=________。

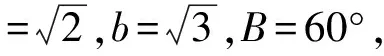
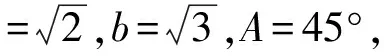
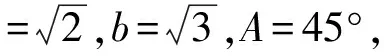
思考1通过4道练习题，你能归纳总结解三角形的几种常见题型及其相应的解法？

思考2三角形的解的个数如何判断？

复习课的目的是引导、帮助学生把已学的知识进行合理串联，通过对知识的再整合、再总结，形成思维导图，从而实现融会贯通。微视频不是简单的知识回顾，而是关注学生在观看过程中对解三角形的理解与思考。通过求解练习复习正弦定理、余弦定理比单纯地复习回顾正弦定理、余弦定理的内容和常见题型有吸引力、时效性。通过解答4道基础练习题，学生进一步掌握4种常见题型的解法。两道变式习题是针对“两边一对角”可能出现无解、一解、两解这个难点设计的，可以诱发学生认知冲突，从而追根溯源，思考出现3种可能结果的原因及判断方法。通过两道思考题完成基本题型与解题方法的系统归纳，体验从特殊到一般的归纳过程。

2.2.2 释疑解惑，交流助学

课堂学习是翻转课堂教学模式的重要环节，是释疑解惑、交流研讨、内化整合的过程。本节复习课将系统梳理全章的知识内容、方法，让学生熟练掌握知识间的内在联系及解三角形的方法与技巧。师生可以围绕以下几个问题展开交流研讨：

1) 在解三角形中，已知哪些元素，可以确定其余元素？

2) 应用正弦定理、余弦定理解三角形时要注意什么问题？

3) 求一个三角形的角，正弦定理、余弦定理均可使用，如何适当选择？有何利弊？

4) 如何应用解三角形的知识解决实际问题？如何将实际问题转化为数学问题？

练习2两灯塔A，B与海洋观察站C的距离都等于akm，灯塔A在C北偏东30°，B在C南偏东60°，则A，B相距________。

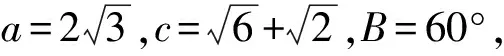
复习课应该高屋建瓴，审视整章知识，形成知识框架，让学生充分体会知识的内在联系，整体感知解三角形的基本思路、过程和方法。通过练习，学生体会如何建模，如何选择正弦定理、余弦定理。交流展示既“展示解题过程”，又展示“学生的思维过程”，不仅让学生充分体验成功解决问题的喜悦，而且让学生深刻、全面了解数形结合、方程与函数、化归与转化等数学思想。

2.2.3 拓展提升，以用促学

“以学定教”是翻转课堂的精髓。不但要复习正弦定理、余弦定理及其在解三角形中的常规应用，更要重视综合性问题，帮助学生提升综合应用能力。通过探究讨论，学生学会分析、归纳、总结，内化知识，拓展思维。

探究1解三角形常与哪些知识交汇命题？

探究2求解与三角形有关的交汇问题的常见思路有哪些？解题的关键是什么？

练习4已知a，b，c分别是△ABC的3个内角A，B，C的对边，

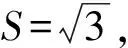
本环节综合练习的设计符合学生认知、思维循序渐进的发展规律，注重方法提炼及思维能力训练，既强化了基础知识和基本技能，又考察了学生综合运用知识的能力。练习4融合了正弦定理、余弦定理、三角变换、基本不等式等基础知识。

2.2.4 总结提炼，课后共学

学生在复习中全面系统认识解三角形，实现知识的系统化、结构化，形成思维导图(见图1)，提高认知能力、归纳能力。通过3道课后练习，进一步巩固复习内容。

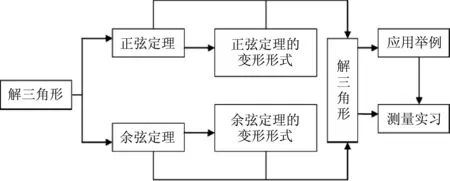
图1 解三角形思维导图

练习5在△ABC中，根据下列条件解三角形，则其中有两个解的是( )。

A.b=10，A=45°，C=70°；

B.a=60，c=48，B=60°；

C.a=7，b=5，A=80°；

D.a=14，b=14，A=45°。

练习6△ABC的3个内角A，B，C成等差数列，

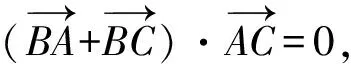
则△ABC的形状是________。

练习7海监艇在某岛南偏西50°相距10 n mile处收到出事船救援信息，出事船正离开该岛沿北偏西10°的方向漂去，漂流时速是2 n mile，海监艇要在1 h内到达出事船位置，问行驶速度至少要多少？

课堂教学结束之后，教师需要对微视频进行编辑，要更加关注学生，遵循学生个性化发展原则，有针对性地布置复习巩固任务，培养学生自主学习能力，进一步完善翻转课堂教学模式。

3 结束语

翻转课堂教学模式下的高三数学复习课，依据学生的实际情况，注重课前自学、把握课中探究、巩固课后提升等，构建了以学生为主体的课堂。翻转课堂有助于学生调控学习，把先学过程中遇到的问题、困惑放到课堂上交流探究、重点突破，提高了课堂上师生、生生的互动性，实现了个性化学习[5-6]。这种课前主动、课上互动的翻转课堂教学模式可以提高教学的有效性。