规律：在探究思辨中建构——“最简分数化成有限小数”错例改进策略探寻

浙江绍兴市嵊州剡溪小学（312400）

“最简分数能否化成有限小数”是人教版教材五年级下册的内容，2012年的修订版教材中已不把这个知识列为正式的教学内容，而是安排阅读材料“你知道吗？”，让学生了解后在练习中适当加以巩固。在期末总复习的测试中有这样一题：“这七个分数中，能化成有限小数的有（ ）个。”学生的错误率较高，最高的班级达到44.7%，最低的班级也有23%，学生认为有限小数有2个或3个的较多。为此，笔者进行了错例研究。

一、访谈记录

【错例1】能化成有限小数的有（2个）。

师：你是怎么想的？

生1：我一个个看，一个个判断。

师：你是怎么判断的？

生1：看分母是不是只有因数2或5。8只有因数2，25只有因数5。因此填了2个。

师：还有什么要注意的吗？

（学生沉默）

师：要不要考虑分数是不是最简分数？

生1：要，我忘记这点了。

【错例2】能化成有限小数的有（3个）。

师：你是怎么思考的？

生2：我是用分子除以分母的方法。

师：除时碰到什么问题了吗？

生2：要除好几次，太麻烦了。

师：是有点麻烦，那你每个分数都除了吗？

生2：因为太麻烦，后面两个就没有再除了，都当成不能的了。

师：老师讲过其他判断的方法吗？

生2：没有。

二、错因追溯

1.教材层面——改为附加阅读

根据课程标准对因数和倍数内容的调整，人教版教材五年级下册第四单元“分数的意义和性质”中“质因数”“分解质因数”“最简分数化成有限小数”等内容，已作为阅读性材料“你知道吗？”

你知道吗?

你知道什么样的最简分数能化成有限小数吗?你想了解这个规律吗?

其实，只要把分数的分母分解质因数，就能知道一个分数能否化成有限小数。

如果分母中除了2和5以外，不含有其他质因数，这个分数就能化成有限小数。

如果分母中含有2和5以外的质因数，这个分数就不能化成有限小数。

“你知道吗？”旨在于拓宽知识的延展性，让学生了解后跳一跳摘到更好的“桃子”。表1就是五年级下册中与“分数的意义和性质”相关的“你知道吗？”。从课本第56页到第79页，短短24页中就出现了6次“你知道吗？”，所涉及的内容都是与这单元内容相匹配的辅助知识。此部分内容对于大部分学生来说自学难度较高，为取得更好的学习效果，教师应在课中进行教学，让学生理解并掌握方法。

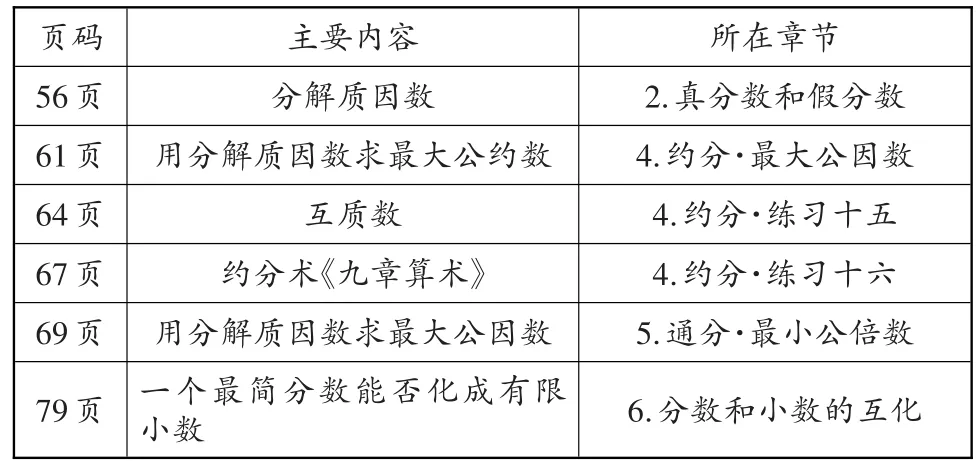
表1 五年级下册“分数的意义和性质”单元中“你知道吗？”内容统计表

2.教师层面——阅读材料起困扰

教材编排上的这些改变给教师带来了一定的困扰：这些“阅读材料”是教还是不教？不教，学生不知道；作为阅读内容在课堂上简略带过，学生模模糊糊，没有印象；作为知识内容教，那得增加课时和工作量。教师指导用书对这部分内容给出的建议是“学生自学与老师指导相结合”。这样的界定是含糊的，教师应该教到哪种程度是不明晰的。这样就导致教师不能准确及适度地把握“阅读材料”的教学要求，在实际教学中没能采用适当的教学措施而导致了学生知识上的缺失。

3.学生层面——自学难

这些阅读材料知识性强，学生难以自主理解，加上阅读材料内容简练，对于具体的方法没有详细的介绍，而只是简单举例，学生要在单个或几个简单的例子中掌握解决问题的方法是非常困难的，因为学生的感知和思维是碎片化的，很难串联起来。如果教师在教学时避而不教或简单带过，学生遇到问题时就只会用常规方法（分子除以分母）尝试解决，过程比较麻烦，容易出错；如果教师扎扎实实地教了，学生在总复习阶段也会忘了“最简分数”这个前提条件，直接根据分母中的质因数来判断，导致错误。

三、策略改进

1.多样探究知规律

（1）种子课上来追问

“分数和小数的互化”的种子课上，在教学分数转化成小数的常规方法即分子除以分母之后，可以增加一个追问环节：“为什么这些分数能转化成有限小数呢？和分子有关？还是和分母有关？这些分母又有什么特点呢？”将“你知道吗？”的内容在这里渗透、拓展，将学生的思维推向更深层次，为种子课增添色彩。

（2）练习课上来拓展

再结合教材的习题：

把下面的分数化成有限小数（不能化成有限小数的保留两位小数）。

引导学生按照能否化成有限小数来分类，并进一步探究：能化成有限小数的分数和不能化成有限小数的分数有什么特点？让学生在思考讨论的基础上阅读教材中的“你知道吗？”，从而了解规律。这样既合乎课程标准的要求——降低了教学难度，给予学生结合实例验证规律的过程，又有效拓展了学生的思维和开阔了学生的视野。

【教学片段】

师：下面的分数哪些能化成有限小数？哪些不能化成有限小数？

生1：能化成有限小数，不能化成有限小数。

师：想一想，能化成有限小数的这些分数有什么特点？

生2：能化成有限小数的分数的分母都是10、100、1000，分母是25、125、20的也能化成有限小数。

生3（迫不及待地）：分母是25、125、20的分数能扩大成分母是100、1000的分数，也能化成有限小数。

师：那么不能化成有限小数的分数又有什么特点？

生4：分母不能扩大成10、100、1000的分数。

师：分母是30、9、6的分数为什么不能扩大成分母是10、100、1000的分数呢？

生5：因为找不到一个与它们相乘会得到10、100、1000的数。

生6：因为30、9、6不是100、1000的约数。

师：30确实不是100、1000的约数。这是因为30里面还有什么？10、100、1000里面不含有什么？

（学生都沉默了）

生7：因为30里面有一个3，10、100、1000里面没有3。

（学生继续沉默）

师：这个问题有点难为大家了。请大家看课本第79页的“你知道吗？”

（学生阅读课本）

师：现在你知道是什么原因了吗？

生8：因为30=2×3×5，除了2和5外，含有质因数3，所以30不能化成有限小数。

生9：9=3×3，6=2×3，9和6也含有质因数3，都不能化成有限小数。

师：分母是25、125、20的为什么能化成有限小数？

生10：因为25=5×5，125=5×5×5，20=2×2×5，它们的分母中只含有质因数2或5，所以能化成有限小数。

师：分母中除了2和5以外，不含有其他的质因数，这个分数就能化成有限小数。而含有2和5以外的质因数，这个分数就不能化成有限小数。想一想，这是为什么？

生11：因为有2和5以外的质因数，就不能扩大成分母是10、100、1000的分数了。

师：大家听明白了吗？谁再来说说。

……

教师提供充足的时间和空间，让学生自主探究规律，在学生的思维受阻时，让学生自主阅读课本材料“你知道吗？”，适度地降低了教学难度。通过对材料的理解和质疑，学生进一步感知了这个规律的内涵。

2.质疑验证明规律

有了第一条顺向思考的策略，再结合反向验证的操作，学生就能知其然并知其所以然。结合种子课和练习课的相关训练，初步让学生了解规律后，教师就要引导学生质疑“这是为什么？”，从而引发学生的头脑风暴。

第一环节：神奇变变变。让学生通过分解10、100、1000等数，直观地感受只含有质因数2和5的事实。

第二环节：破坏加加加。让学生加入其他的质因数，“搞破坏”，导致那些数永远成不了整十、整百、整千的数。

第三环节:超级转转转。让学生感知只有分母是整十、整百、整千的数才能转化成有限小数。

这三大环节就能使学生明确最简分数的分母中只有含有质因数2和5的分数能转化成分母是10、100、1000的分数，能转化成有限小数；分母中含有2和5以外的质因数就不能转化成分母是10、100、1000的分数，也就不能转化成有限小数了。在学生知其所以然的基础上，教师再让学生尝试着自己举例来验证这个规律，自然就能提升学生的思维能力。

3.巩固拓展用规律

有了补充教学，就可以让学生在练习中结合具体内容，自主综合运用。教师只需要出示分数让学生运用规律来判断其能否化成有限小数，并说明理由即可。这样，学生就能进一步明确“最简分数”这个前提，并能熟练应用这个规律来解决问题，提升了自身的思维能力和解决问题的能力。

站在学生的角度去探寻错误的源头，分析错误成因，思索消灭错误的策略，沿着这样的路径，我们有效地达成了“最简分数转化成有限小数”规律的建模目标，真正让学生在自主探究和思辨感悟中破茧成蝶。