对一节计算教学课的思考
2018-12-26江苏如东县马塘镇王元小学226401
江苏如东县马塘镇王元小学(226401)
近日观摩了一堂校内公开课,内容是苏教版教材三年级“两位数乘两位数”。教师首先展示情境图,启发学生通过读图提取信息,然后询问图中透露的信息。学生回答:“订一份学生奶,每月28元,一年需要多少元?”接着,教师要求学生列式计算。汇报展示时,教师随机抽取三名学生上台板演,他们不约而同地用竖式演算。
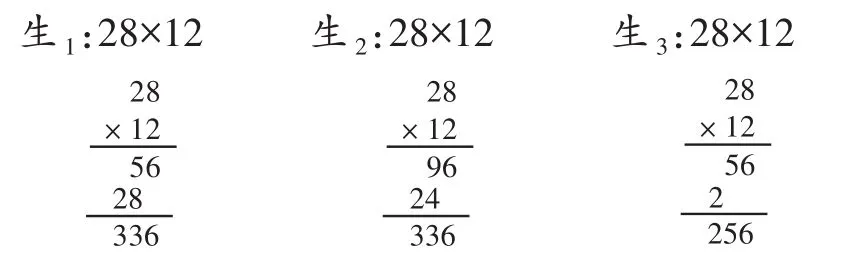
全班反馈交流时,教师评价生2的做法:“虽然结果也是336,但计算方法有误,值得商榷。”其他学生纷纷发表自己的看法,但赞同的少,反对的多。这时,教师小结:“虽然生2的计算结果正确,但计算方法有误,同学们应向生1看齐,计算两位数乘两位数时,应将第二个乘数拆分,这样就可以用我们学过的两位数乘一位数求解,即拆分乘数12,先用2乘28,再用10乘28……”接着,教师用所谓“正规方法”的标尺来评价生3的竖式,并着重指出错处和造成错误的原因。最后,教师又重新演示了一道标准竖式作为模板,并用红色粉笔标注每一步的计算过程。
一、改变算序,异曲同工
在课后访谈时,我们和授课教师、生2进行面对面交流,生2陈述了自己的演算过程:“我分两步计算,先用8乘12,得到96,再用20乘12,得到240,最后累计96+240=336(元),就是一年需要的钱。”
我们仔细斟酌和推敲,生2的思路虽然很特别,但其实也符合算理,与所谓的“正规方法”有异曲同工之妙。
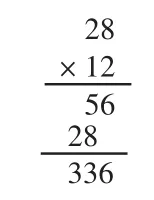
图1

图2
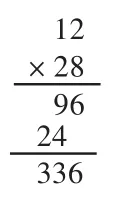
图3
对于生1的“正规方法”(如图1),算理分解如下:把12个月分为2个月和10个月,第一步计算2×28=56,即2个月所需的钱;第二步计算10×28=280,即10个月所需的钱,最后由56+280=336(元),就能知道一年所需的钱。
对于生2的做法(如图2),算理分解如下:把28元分为8元和20元,第一步计算8×12=96,表示每月月头征收8元订金,12个月就是96元;第二步计算20×12=240,表示每月月末征收20元尾款,12个月就是240元,因此12个月的订金和尾款合起来就是96+240=336(元)。
以上两种算法,其实就是乘法分配律的竖排版,生2的做法应该交换两个乘数位置(如图3),这样看来更合理。换言之,生2的算法在算术和算理上都是过关的,只是生2使用的格式不同于常规,容易引起他人误会。
二、谁乘谁,并无分别
案例中,授课教师之所以极力否定生2的算法,并不是教师本人不理解,归根结底,其实是教师在极力维护自己的权威,维护传统的权威。多年来积累的竖式“经验”让教师墨守成规,也可以说,按照这种经验从未出错,所以对其深信不疑。
当然,我们不能把原有经验一棍子打死,但我们可以在充分尊重原有经验的基础上,去鉴别和接纳“经验”以外的新鲜事物,吐故纳新,不断保持生命力。教学时,如果教师能慢下来,耐心倾听学生的心声,那么教师和其他学生都会受到启发,有所发展。
其实,新型算法正体现了生2对乘法竖式结构深入细致的认知。在用竖式计算多位数乘以一位数时,自上而下和自下而上本身没什么区别,如计算“124×3”时,第一步计算4乘3或3乘4其实没什么不同,都是同一句口诀,只是感觉上有先后差别而已。这是生2当时的心理状态,但没引起授课教师的注意。
三、经验之后,孕育创新
在教学“用竖式计算124×3”后,教师通常都是照本宣科,提出用交换律来验算,但验算的目的仅仅在于结果的一致性,对于“竖式验算时,交换两个乘数的位置,乘积为什么不变”没有进行深入的思考。如果教师能打破常规,在学生发出“不和谐”的声音时,以包容的姿态,大大方方让新方法和旧方法来一次正面交锋,就会促进学生的认知更有深度。
要想进步,经验必不可少,经验也是教师走向成熟的重要条件,但任何经验都是一把双刃剑,它是发展变化的,如果因循守旧、无视甚至排斥这种改变,那么就会搬起石头砸自己的脚。
