类矩形盾构隧道横向刚度有效率分析
2018-12-18丁祖德付江王志良郭永发李向红
丁祖德,付江,王志良,郭永发,李向红
类矩形盾构隧道横向刚度有效率分析
丁祖德1,付江1,王志良1,郭永发2,李向红3
(1. 昆明理工大学 建筑工程学院,昆明 650500; 2. 中铁二院昆明勘察设计研究院有限责任公司,昆明 650200; 3. 上海隧道工程股份有限公司,上海 200232)
基于变形等效,建立类矩形盾构管片结构梁-接头模型,研究通缝、错缝拼装下类矩形盾构隧道横向刚度有效率。分析地基抗力系数、接头刚度比及接头数量对刚度有效率的影响,并建立了类矩形盾构隧道刚度有效率计算公式。研究结果表明:通缝、错缝拼装下管片结构横向刚度有效率平均值分别为0.47和0.54,错缝比通缝提高约15%。刚度有效率随地基抗力系数的增加呈非线性增长,随接头刚度比的增大呈线性增长,随接头数量的增加呈线性减小。类矩形盾构管片横向刚度有效率在0.3~0.8之间变化。建立的刚度有效率计算公式拟合精度高,可为类矩形盾构隧道结构计算提供依据。
类矩形盾构隧道;梁-接头模型;横向刚度有效率;影响因素
随着城市地下空间的深入发展,不同功用盾构隧道也随之出现,断面形式不再局限于传统的圆形盾构隧道,双圆形、类矩形等新兴盾构隧道断面形式逐渐引入并得到应用[1−9]。对于城市地铁车站出入口、跨越路口、地下综合管廊等特殊节点,矩形盾构隧道在空间利用率、长距离曲线掘进等方面有明显优势。自我国宁波轨道交通3号线某车站出入段工程采用类矩形盾构隧道以来,类矩形盾构技术及其装配式衬砌结构计算方法、受力性能等研究日渐重要,已引起广泛关注[4−10]。盾构法隧道衬砌是管片通过螺栓连接的装配式结构,接头的存在是其显著特征。为考虑接头的影响,国内外学者提出了多种计算模型,如修正均质圆环模型(修正惯用法)、多铰环模型、梁-接头模型及壳−弹簧−接触模型 等[11−12]。修正惯用法因其概念明确、计算简便,是盾构隧道结构设计的常用计算方法,其建模的关键在于确定横向弯曲刚度有效率。为此,国内外学者从理论分析、数值计算并结合室内试验,在刚度有效率的取值及影响因素等方面开展了研究[13−17]。如Lee等[13]采用弹性铰模型,得到通错缝拼装情况下盾构隧道横向刚度有效率与管片特征、地层抗力系数等参数的拟合关系,指出软土地区隧道刚度有效率在0.1~0.6之间。黄宏伟等[14]基于管片结构室内模型加载试验,得出隧道结构变形与荷载明显呈线弹性关系,隧道刚度有效率可取为常数。封坤 等[15]开展狮子洋隧道和南京长江隧道结构整环原型试验,得到通、错缝拼装情况下2个典型盾构隧道的刚度有效率范围。李晓军等[16]基于横向变形等效原则,结合通缝单环梁−接头模型和错缝双环梁−接头模型,分析大直径盾构隧道结构刚度有效率随埋深的变化规律。黄大维等[17]依据纵缝接头刚度和横向弯曲刚度有效率之间的关系,推导依据接头刚度计算通缝拼装盾构隧道横向刚度有效率的计算公式,分析各因素对刚度有效率的影响规律。上述研究均是针对圆形盾构隧道,而矩形盾构隧道横向刚度有效率的取值,多借鉴圆形盾构隧道,凭经验判断,尚未有类矩形盾构隧道横向刚度有效率研究的报道。基于此,本文以某曲墙曲拱类矩形盾构隧道装配式衬砌结构为研究对象,参考类矩形管片接缝受力试验结果,建立梁−接头模型,研究通缝和错缝2种拼装方式下类矩形盾构隧道横向刚度有效率。在此基础上,研究地层抗力系数、接头刚度比、接头数量等因素对类矩形盾构隧道横向刚度有效率的影响规律,并建立刚度有效率计算公式,为类矩形盾构隧道结构设计计算提供参考依据。
1 计算模型及参数
1.1 类矩形盾构管片简介
本文探讨的类矩形断面形式借鉴文献[4−5],以2车道城市道路隧道作为运用背景,采用曲墙曲拱断面2车道拼装式衬砌的类矩形盾构隧道管片结构。以《城市道路工程设计规范》(CJJ37—2012)为依据,隧道建筑限界及衬砌内轮廓如图1所示,其最大跨度9.95 m,净高6.8 m。考虑管片结构受力、施工条件、管片拼装及防水要求,拟定管片厚度为50 cm,环宽为1.5 m,管片分块数量为10块。采用错缝拼装,将类矩形盾构装配式衬砌分为甲组管片和乙组管片,隧道纵向环与环之间按照“甲−乙−甲”的方式进行拼装。管片间接缝采用螺栓连接,包括40个M33环向螺栓和30个M30纵向螺栓,螺栓机械性能等级为6.8级。
1.2 横向刚度有效率计算方法
依据修正惯用法中横向刚度有效率的定义,其可表示为:
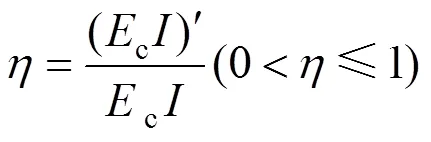
式中:(c)'表示非均质圆环的等效抗弯刚度;c表示均质圆环的横向抗弯刚度。
对圆形盾构隧道而言,文献[18]基于变形等效,假定圆环直径为,在荷载作用下,变形后的非均质圆环直径为1,直径变化量为Δ1;变形后的均质圆环直径为2,直径变化量为Δ2。得出横向刚度有效率为:

实际上,式(2)忽略了变形的相对性问题,不符合刚度有效率的定义,计算结果也与实际不符。根据《盾构隧道管片设计》[11],在垂直均布荷载作用下,当考虑地层反力,可推导出管片环水平直径点的水平位移为:

式中:s为地基抗力系数;c为管片壁厚中心半径;为管片环所受均布荷载。
从式(3)可知,若周边地层较好,地基抗力系数较大,则管片结构变形基本受地层约束作用影响,管片刚度的影响较小,这也说明在地层条件较好情况下,可将接缝处视为铰接,按圆环铰模型来计算。对于软黏土或砂土地层,地层抗力系数较小,管片刚度的影响则较明显,按梁-接头模型计算较合适。若不考虑地层反力,依式(3)可推导出均质环水平直径点的水平位移1为:

同理,考虑接头的管片环水平直径点水平位移2可表示为:

由式(4)和式(5)可得出:
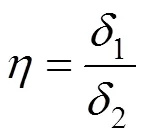
对于类矩形盾构管片结构,采用与上述相同的思路,即在相同荷载作用下,考虑接缝的管片结构和等效后均质管片的变形相等时,认为两者刚度相同,由此得到其刚度有效率。考虑类矩形断面竖向和水平向刚度的差异,建立如图2所示刚度有效率计算模型,竖向刚度有效率z和水平向刚度有效率η分别定义为:
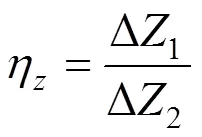
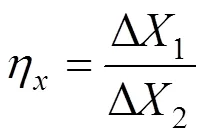
式中:Δ1表示均质结构竖向位移变形量;Δ2表示考虑接头的结构竖向位移变形量;Δ1表示均质结构水平向位移变形量;Δ2表示考虑接头的结构水平向位移变形量。
(a) 均质类矩形结构;(b) 考虑接缝类矩形结构
图2 横向刚度有效率计算模型
Fig. 2 Calculation models for transverse effective rigidity ratio
按图2的荷载模式,等比例增大竖向荷载、水平荷载和底部荷载,得到不同荷载工况下类矩形结构的变形值,再根据式(7)和式(8)可计算出刚度有效率。
1.3 计算模型及参数
采用荷载−结构法,分别建立单环均质模型、通缝拼装下的单环梁-接头模型和错缝拼装下的双环梁−接头模型。采用梁单元模拟管片,转动弹簧和剪切弹簧模拟管片接头。其中,管片接缝处转动刚度K表示为[11]:


式中:b为螺栓的有效断面面积;为管片主体与螺栓的弹性模量比;表示管片宽度;d表示有效高度;c为混凝土弹性模量;为管片高度;表示中和轴到管片受压边缘的距离;表示弯矩;表示转角。
由式(10)算出的管片接头转动弹簧系数为122.4 MN·m/rad。参照类矩形盾构隧道管片纵缝抗弯性能试验结果[8],正、负弯矩转动刚度在70~120 MN·m/rad,多集中在100~120 MN·m/rad。故本处取管片接头转动弹簧系数为120 MN·m/rad。
在类矩形盾构隧道纵缝受剪性能试验中,得到的纵缝抗剪刚度范围为350~450 MN/m[9]。管片环间的径向剪切刚度一般取值在100~500 MN/m之间[11],本处综合取径向剪切弹簧刚度为300 MN/m,不考虑切向剪切弹簧刚度。
地基抗力系数s可采用考虑隧道半径影响的解析解[16]:

式中:为地基弹性模量;为泊松比;0为类矩形盾构隧道等效半径。取地基弹性模量为15 MPa,算出地基抗力系数为1.636 MN/m3。考虑注浆后周围土层刚度的提高,并结合《基坑工程手册》的经验值,取地基抗力系数为5 MN/m3。
C50管片混凝土弹性模量为3.45×104MPa,泊松比为0.2,重度为26 kN/m3;接头螺栓弹性模量为2.06×105MPa,泊松比为0.3。计算时,取隧道埋深为5 m,假定为单一均质土层,天然重度取18 kN/m3,侧压力系数取为0.5。
2 横向刚度有效率计算结果分析
以1.3节确定的荷载为基准荷载,分别取0.5倍及1倍~4倍的基准荷载作为加载工况1~5,得到不同荷载工况下,均质结构、通缝及错缝拼装盾构管片的变形见图3,为展现结构变形形态,将变形值放大了50倍。竖向和水平向变形随荷载的变化曲线见图4。横向刚度有效率计算结果见表1。
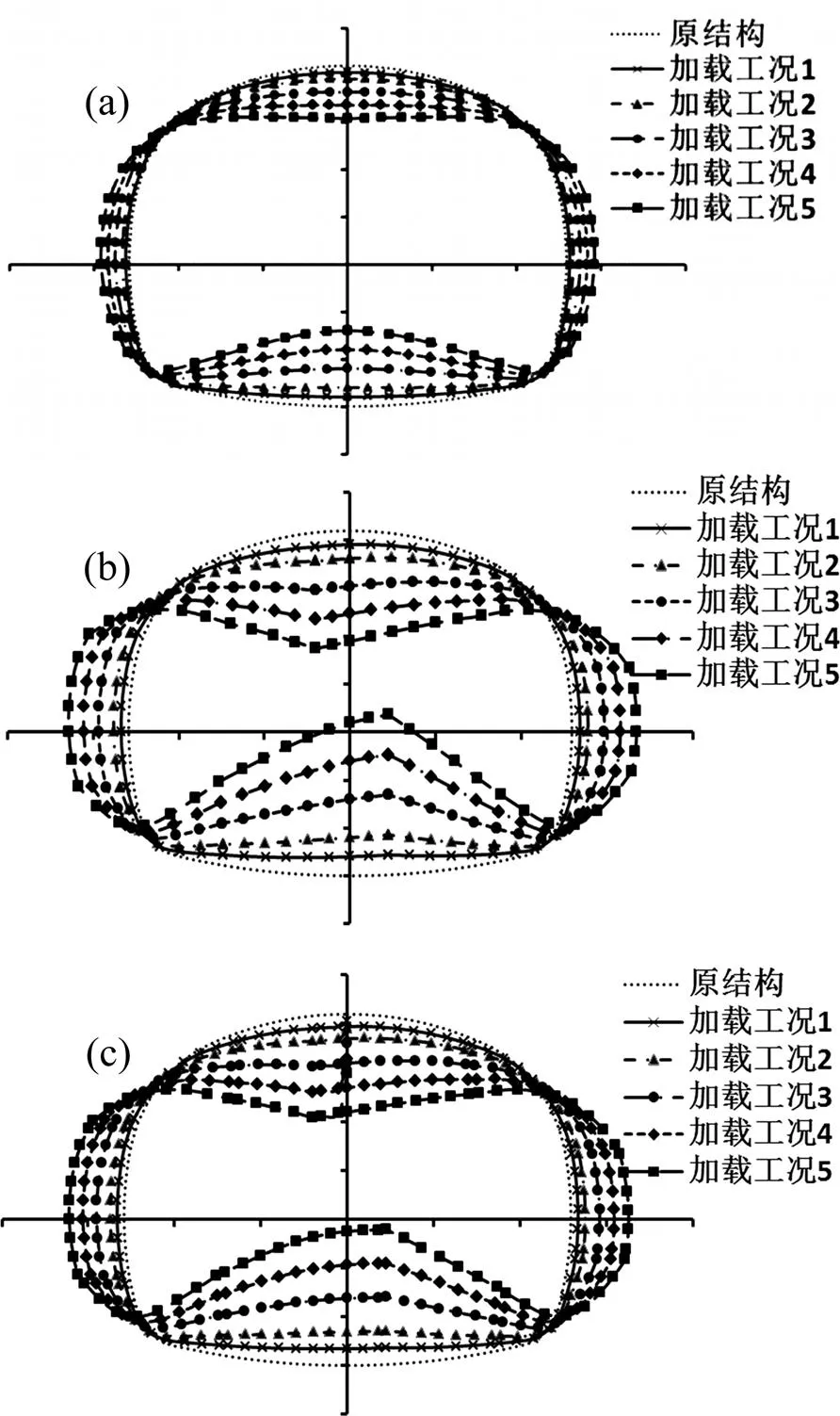
(a) 均质;(b) 通缝拼装;(c) 错缝拼装
从图3看出,采用均质模型与梁−接头模型模拟得到的结构变形轮廓形状有所不同,不考虑接头的均质单环变形轮廓线十分平顺,变形沿管片中轴线对称分布,而考虑接头的通缝、错缝管片变形轮廓线都在接缝处呈现明显折角,管片底部变形呈现不对称分布。管片竖向变形明显大于横向变形,通缝型管片变形量最大,图4中也显示了不同模型下的这种变形差异。通缝拼装下,计算得到的竖向和水平向刚度有效率分别为0.49和0.45,明显小于圆形盾构隧道管片结构的横向刚度有效率。错缝拼装下的竖向和水平向刚度有效率分别为0.57和0.51,较通缝拼装情况分别提高了16%和13%。

(a) 竖向;(b) 水平向

表1 类矩形盾构隧道横向刚度有效率
计算结果显示,与常规地铁盾构隧道刚度有效率相比,类矩形盾构隧道管片结构刚度有效率较明显偏小,主要是由于文中类矩形隧道跨度较大、地基抗力系数取值较小,加之隧道断面形式为矩形,受力条件没有圆形断面好,因而计算得到的刚度有效率偏小。这正说明隧道刚度有效率大小与诸多因素相关,应结合隧道具体特征来确定。
3 横向刚度有效率影响因素分析
3.1 地基抗力系数的影响
为考虑地基抗力系数s的影响,改变类矩形管片结构梁−接头模型的地基抗力系数,分别取为5,10,20,30,40,50,70和100 MPa/m,得到类矩形盾构隧道横向刚度有效率随地基抗力系数的变化曲线如图7所示。

(a) 竖向;(b) 水平向
图5显示,刚度有效率随地基抗力系数的增加呈非线性增长,在地基抗力系数较小时,刚度有效率变化明显,当地基抗力系数达到一定值后,变化放缓。以通缝拼装下刚度有效率为例,当地基抗力系数从5 MPa/m增加到50 MPa/m时,管片竖向、水平向刚度有效率分别增加了37%和58%;从50 MPa/m到100 MPa/m变化时,分别仅增加了6%和14%。错缝与通缝相比,竖向的刚度有效率提高程度随地基抗力系数的增加变化较小,但水平向的刚度有效率提高程度随之减小。在地基抗力系数达到100 MPa/m,2种拼装下的刚度有效率基本接近,说明地层条件越好,拼装方式对结构刚度有效率的影响越小。总体而言,改善地层条件能有效的减少类矩形隧道变形,提高结构的刚度有效率。
3.2 接头刚度比的影响
管片厚度、接头刚度的影响可通过引入接头抗弯刚度与管片抗弯刚度之比,即接头刚度比来 反映[18]:
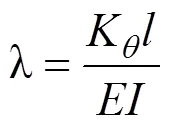
式中:K为管片间旋转弹簧刚度;为管片环宽。
分别取为0.2,0.25,0.3,0.34,0.4和0.5,得到接头刚度比与横向刚度有效率的关系曲线见图8。

(a) 竖向;(b) 水平向
图6表明,随着接头刚度比的增大,管片结构的横向刚度有效率呈线性增长。当从0.2增大到0.5时,通缝拼装下的竖向、水平向刚度有效率分别从0.38和0.35增加到0.58和0.54,增幅分别为53%和54%;错缝拼装下的分别从0.50和0.44增加到0.64和0.59,增幅分别为28%和34%。
3.3 接头数量的影响
分别取管片分块数量为9~11,得到刚度有效率随管片数量的变化曲线如图7所示。
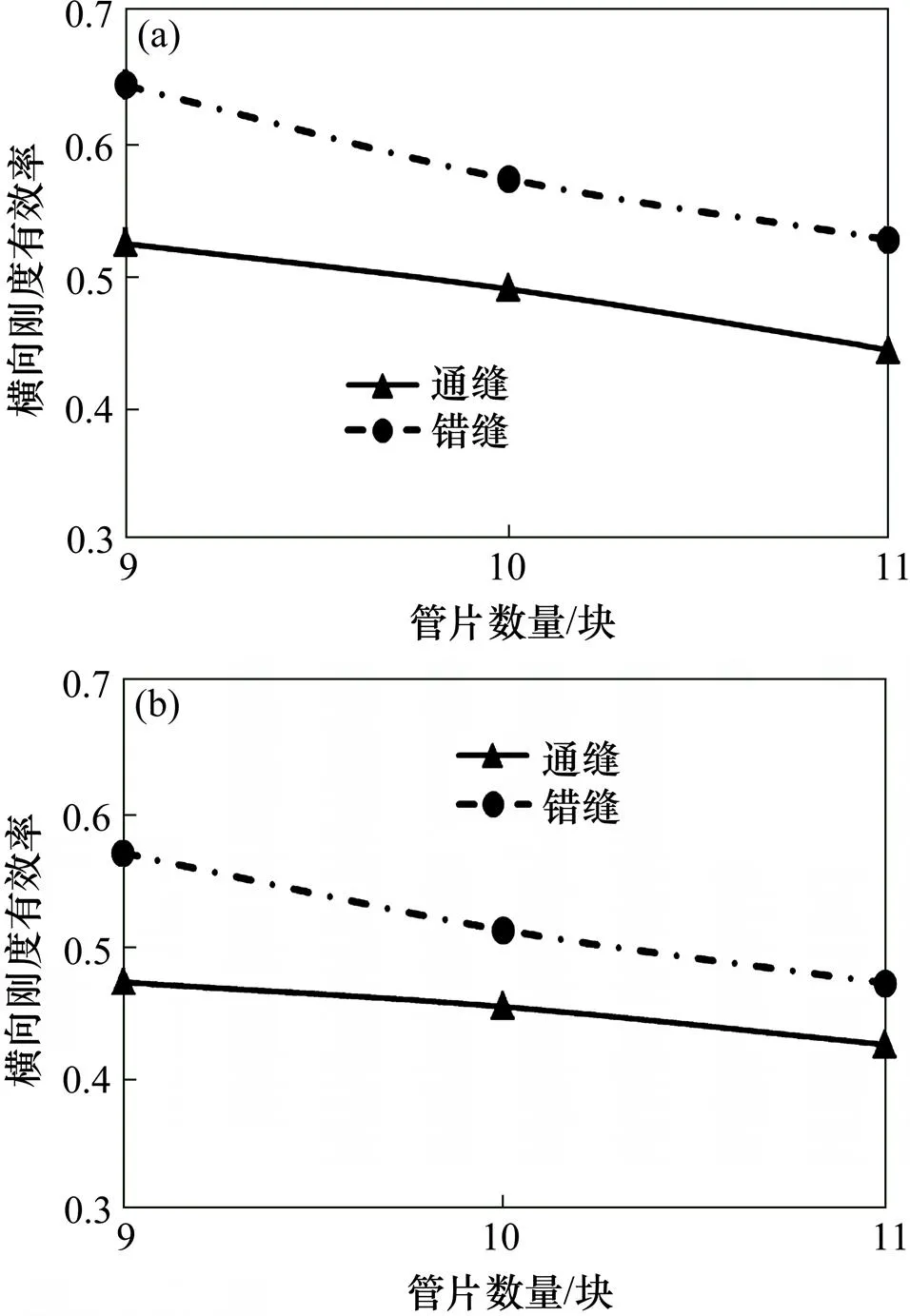
(a) 竖向;(b) 水平向
图7显示,随着接头数量的增加,管片结构横向刚度有效率呈线性减小。每增加一个接头数量,通缝拼装下的刚度有效率平均降幅8%左右,错缝拼装下的降幅10%左右。增加接头数量即接缝数量增多,势必会减少结构的整体刚度。
3.4 刚度有效率拟合公式
为方便应用,建立考虑地基抗力系数、接头刚度比和接头数量的刚度有效率计算表达式如下:

式中:为接头数量;14为拟合参数。
通过对回归分析得到拟合系数取值见表2。
由表2可知,2种拼装方式下,类矩形管片结构刚度有效率拟合公式相关系数均超过0.9,具有较高相关性。其中,刚度有效率与地基抗力系数、接头刚度比呈现正相关,而与接头数量呈负相关性。该拟合公式可为类矩形盾构隧道结构刚度有效率的取值提供有益参考。

表2 横向刚度有效率计算拟合参数
4 结论
1) 基于变形等效和类矩形管片纵缝试验结果,建立通缝和错缝2种拼装方式下的类矩形盾构管片结构梁−接头模型,得出通缝下管片结构横向刚度有效率平均值为0.47,错缝拼装下为0.54,较之提高约15%。
2) 横向刚度有效率影响因素分析表明:刚度有效率随地基抗力系数的增加呈非线性增长,随着接头刚度比的增大呈线性增长,随着接头数量的增加呈线性减小。在常见地层条件、管片结构和接头型式下,类矩形盾构管片横向刚度有效率在0.3~0.8之间变化。改善地层条件、增大接头刚度比和减少接头数量,能有效提高结构的刚度有效率。
3) 建立2种拼装方式下,类矩形管片结构刚度有效率拟合公式,拟合结果显示计算公式具有较高相关性,可为类矩形盾构隧道结构刚度有效率的取值提供有益参考。
[1] 袁金荣, 周裕倩, 刘学增, 等. 双圆盾构隧道衬砌结构设计及参数研究[J]. 岩土工程学报, 2005, 27(6): 638− 641. YUAN Jinrong, ZHOU Yuqian, LIU Xuezeng, et al. Structural design of lining and parameter analysis for DOT shield tunnel[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(6): 638−641.
[2] 胡欣雨, 张子新. 双圆盾构隧道衬砌不同内力计算模型对比分析[J]. 地下空间与工程学报, 2007, 3(1): 44−49. HU Xinyu, ZHANG Zixin. Comparison and analysis of different computational models of internal force for dot shield-driven tunnel lining[J]. Chinese Journal of Underground Space and Engineering, 2007, 3(1): 44−49.
[3] 季昌, 周顺华, 朱瑶宏, 等. 类矩形盾构壳体与土相互作用下周边地层变形模式[J]. 岩石力学与工程学报, 2017, 36(增刊): 3644−3655. JI Chang, ZHOU Shunhua, ZHU Yaohong, et al. Surrounding strata deformation pattern under the interaction between shell of quasi-rectangular shield and soft soil[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(Suppl): 3644−3655.
[4] 李向红. 类矩形盾构隧道装配式衬砌结构设计参数研究[J]. 地下工程与隧道, 2017(1): 21−25, 57. LI Xianghong. Study on design parameters of assembled lining structure of quasi-rectangular shield tunnel[J]. Underground Engineering and Tunnels, 2017(1): 21−25, 57.
[5] 李向红. 结构参数对异形断面盾构隧道管片力学特性的影响研究[J]. 施工技术, 2017, 46(8): 68−71. LI Xianghong. Effects of structural design parameters on mechanical behavior of lining segment for special section shield tunnel[J]. Construction Technology, 2017, 46(8): 68−71.
[6] 朱雁飞, 刘震, 叶宇航, 等类矩形盾构隧道结构计算方法研究[J]. 现代隧道技术, 2016, 53(增1): 128−135. ZHU Yanfei, LIU Zhen, YE Yuhang, et al. Structural calculations of quasi-rectangular shield tunnels[J]. Modern Tunneling Technology, 2016, 53(Suppl 1): 128− 135.
[7] 叶宇航, 黄德中, 李刚, 等. 类矩形盾构隧道衬砌结构极限承载力足尺试验研究[J]. 现代隧道技术, 2016, 53(增1): 118−127. YE Yuhang, HUANG Dezhong, LI Gang, et al. Full scale experimental study on the ultimate bearing capacity of quasi-rectangular shield tunnel lining[J]. Modern Tunneling Technology, 2016, 53(Suppl 1): 118−127.
[8] 朱瑶宏, 张维熙, 董子博, 等. 类矩形地铁盾构隧道纵向接缝受力性能对比研究[J]. 铁道科学与工程学报, 2017, 14(6): 1278−1286. ZHU Yaohong, ZHANG Weixi, DONG Zibo, et al. Comparative study on the mechanical performance of longitudinal joint in quasi-rectangular segmental tunnel lining[J]. Journal of Railway Science and Engineering, 2017, 14(6): 1278−1286.
[9] 柳献, 张维熙, 王东方. 类矩形盾构隧道纵缝受剪性能试验研究[J]. 铁道科学与工程学报, 2016, 13(9): 1767−1775. LIU Xian, ZHANG Weixi, WANG Dongfang. Experimental study on shear performance of longitudinal joint in quasi-rectangular shield tunnel[J]. Journal of Railway Science and Engineering, 2016, 13(9): 1767− 1775.
[10] 司金标, 朱瑶宏, 季昌, 等. 软土层中类矩形盾构掘进施工引起地层竖向变形实测与分析[J]. 岩石力学与工程学报, 2017, 36(6): 1551−1559. SI Jinbiao, ZHU Yaohong, JI Chang, et al. Measurement and analysis of vertical deformation of stratum induced by quasi-rectangular shield tunneling in soft ground[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(6): 1551−1559.
[11] 小泉淳. 盾构隧道管片设计—从容许应力设计法到极限状态设计法[M]. 官林星, 译. 北京: 中国建筑工业出版社, 2012. ATSUSHI Koizumi. Shield tunnel design: From allowable stress design method to limit state design method[M]. GUAN Linxing, trans. Beijing: China Architecture and Building Press, 2012.
[12] 苏宗贤, 何川. 盾构隧道管片衬砌内力分析的壳−弹簧−接触模型及其应用[J]. 工程力学, 2007, 24(10): 131− 136. SU Zongxian , HE Chuan. Shell-spring-contact model for shield tunnel segmental lining analysis and its application[J]. Engineering Mechanics, 2007, 24(10): 131−136.
[13] Lee K M, GE X W. The equivalence of a jointed shield- driven tunnel lining to a continuous ring structure[J]. Journal of Canadian Geotechnical Engineering, 2001, 38: 461−483.
[14] 黄宏伟, 徐凌, 严佳梁, 等. 盾构隧道横向刚度有效率研究[J]. 岩土工程学报, 2006, 28(1): 11−18. HUANG Hongwei, XU Ling, YAN Jialiang, et al. Study on transverse effective rigidity ratio of shield tunnles[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(1): 11−18.
[15] 封坤, 何川, 夏松林. 大断面盾构隧道结构横向刚度有效率的原型试验研究[J]. 岩土工程学报, 2011, 33(11): 1750−1758. FENG Kun, HE Chuan, XIA Songlin. Prototype tests on effective bending rigidity ratios of segmental lining structure for shield tunnel with large cross-section[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(11): 1750−1758.
[16] 李晓军, 黄伯麒, 杨志豪, 等. 不同埋深下大直径盾构隧道横向刚度有效率[J]. 同济大学学报(自然科学版), 2015, 43(8): 1159−1166. LI Xiaojun, HUANG Boqi, YANG Zhihao, et al. Lateral equivalent stiffness of large diameter shield tunnel lining structure at various buried depths[J]. Journal of Tongji University (Natural Science), 2015, 43(8): 1159−1166.
[17] 黄大维, 周顺华, 冯青松, 等. 通缝拼装盾构隧道横向刚度有效率计算方法及其影响因素[J]. 中国铁道科学, 2017, 38(3): 47−54. HUANG Dawei, ZHOU Shunhua, FENG Qingsong, et al. Calculation method for transverse effective rigidity ratio of shield-driven tunnel with straight joint and its influential factors[J]. China Railway Science, 2017, 38(3): 47−54.
[18] Yukinori Koyama. Present status and technology of shied tunneling method in Japan[J]. Tunneling and Underground Space Technology, 2003(18): 145−149.
(编辑 阳丽霞)
Analysis of transverse effective rigidity ratio of quasi-rectangular shield tunnel
DING Zude1, FU Jiang1, WANG Zhiliang1, GUO Yongfa2, LI Xianghong3
(1. Faculty of Civil Engineering and Mechanics, Kunming University of Science and Technology, Kunming 650500, China; 2. Kunming Survey, Design and Research Institute Company Limited of CREEC, Kunming 650200, China; 3. Shanghai Tunnel Engineering Company Limited, Shanghai 200232, China)
Based on the deformation equivalent, the effective rigidity ratio of quasi-rectangular shield segment with straight and staggered assembling was studied by using the beam-joint model. The influences of soil resistance coefficient, bending stiffness ratio and number of joints on the transverse effective rigidity ratio were analyzed. In addition, an evaluation formula of transverse effective rigidity ratio was established for quasi-rectangular shield tunnel. The results show that the average effective rigidity ratios of rectangular tunnel with straight and staggered assembling are 0.47 and 0.54 respectively, the staggered pattern is about 15% higher than the straight pattern. It increases nonlinearly with the increase of soil resistance coefficient; it increases linearly with the increase of bending stiffness ratio and decreases linearly with the increase of the number of joints. Its numerical value varies between 0.3 and 0.8. The formula of effective rigidity ratio has high precision and can be used in rectangular tunnel engineering practice.
quasi-rectangular shield tunnel; beam-joint model; transverse effective rigidity ratio; influence factor
10.19713/j.cnki.43−1423/u.2018.12.022
U451
A
1672 − 7029(2018)12 − 3181 − 08
2017−11−13
国家自然科学基金资助项目(51768028,51308270)
丁祖德(1979−),男,湖南汉寿人,副教授,博士,从事隧道与地下结构方面的研究;E−mail:dzdvsdt@163.com
