桥隧过渡段实腹式RC拱桥上无缝线路纵向力分布特征
2018-12-18于向东李毓坤闫斌
于向东,李毓坤,闫斌
桥隧过渡段实腹式RC拱桥上无缝线路纵向力分布特征
于向东1,李毓坤2,闫斌1
(1. 中南大学 土木工程学院,湖南 长沙 410075; 2. 湖南省交通规划勘察设计院有限公司,湖南 长沙 410008)
以西成高铁52 m实腹式RC拱桥为例,建立考虑CRTS I型双块式无砟轨道结构的钢轨−道床板−实腹式钢筋混凝土拱桥三维实体模型,研究其无缝线路纵向力分布特征;在此基础上,探讨隧道的遮挡作用下钢轨、道床板的纵向温差对无缝线路纵向力的影响;以及长期收缩徐变作用下主拱圈分层施工对桥上无缝线路纵向力的影响。研究结果表明:拱桥伸缩力最大值出现在跨中,且数值较大,为主要控制性荷载;桥梁两端隧道遮挡作用对钢轨应力影响明显,不同道床板纵向温差条件下,钢轨应力增幅为1.0%~5.5%,钢轨纵向位移最大增幅14.8%;钢轨纵向温差条件下,钢轨应力与纵向位移较大,设计时应予以重视;考虑混凝土10 a收缩徐变的影响,主拱圈分层施工与一次浇筑相比,钢轨压应力减小20.6%,钢轨纵向位移减小14.9%。
实腹式拱桥;无缝线路;钢轨纵向力;桥隧过渡段;收缩徐变
木河中桥位于西成高铁陕西境内秦岭深处的木河之上,地质复杂,该桥采用钢筋混凝土实腹式拱桥的形式,在高速铁路上的应用尚属首次。其构造简单、刚度大、造价低、施工方便,但由于混凝土用量大,故受到收缩徐变影响也较大。在梁轨相互作用方面,尽管国内外许多学者[1−3]对混凝土简支梁桥,斜拉桥和连续梁桥的纵向力进行了大量的研究,但对于实腹式拱桥的桥上纵向力研究仍较为匮乏[4],以及大体积混凝土的收缩徐变、隧道遮挡作用引起的钢轨温差与道床板温差对钢轨的影响尚不明确。本文以西成客专52 m钢筋混凝土实腹式拱桥为例,考虑其大体积混凝土的实际特性,采用通用有限元软件建立钢轨−道床板−底座板−实腹式拱桥的空间实体单元模型,两边各建立100 m轨道以准确模拟边界条件[5]。在此基础上,分析桥隧过渡段实腹式钢筋混凝土拱桥纵向力分布规律,探讨由于两端隧道遮挡效应引起的钢轨和道床板温差对无砟轨道纵向力的影响,以及在长期收缩徐变作用下主拱分层施工对桥上无砟轨道纵向力的影响。
1 梁轨计算模型与参数
1.1 工程背景
木河中桥主拱跨径52 m,主拱圈采用钢筋混凝土等截面矩形板拱,矢高13 m,矩形板拱截面宽9 m,高2.5 m。拱上建筑为混凝土实体截面,左右两侧各有4个深2.4 m的装饰拱。桥上铺设双线CRTS I双块式无砟轨道,线距4.6 m,桥梁两端均为隧道结构。
桥上双块式无砟轨道的底座板通过梁体预埋钢筋与桥梁连接,使底座板与桥梁连成一个整体。底座板上设置凹槽,实现道床板的纵横向限位,凹槽侧面及顶面设置弹性垫层,以缓冲道床板对底座板的震动作用,底座顶面设置隔离层。道床板将承受的列车荷载、温度荷载通过凸台传递至底座板,进一步传至桥梁[6],拱桥总体布置见图1。

单位:m
1.2 计算模型与参数
计算模型中,钢轨为CHN60型钢轨,采用纵向连续的梁单元模拟。扣件采用WJ-8型扣件,扣件间距0.65 m,扣件竖向刚度取35 kN/mm[6],采 用线性弹性连接模拟,其纵向力−位移关系可表 示为[3]:

式中:为扣件纵向阻力,(kN/m)/轨;为钢轨相对于扣件的纵向位移,mm。采用非线性弹性连接模拟。
空间梁单元桥梁模型不能很好地反映高速铁路实腹式拱桥的空间力学特性,用空间梁单元桥梁模型计算挠曲力有较大的误差。另一方面,横向刚臂刚度很大,与横向刚臂连接各点具有几乎相同的转角,导致桥梁顶板同一断面各点纵向位移几乎相等,不能很好反映双线铁路桥梁、轨纵向相互作 用[7],基于此原因,本文没有采用空间梁单元桥梁模型,全部采取空间实体单元模拟桥梁。全桥共使用实体单元32 200个。
桥上采用道床板加底座板的结构,道床板与底座板之间设置隔离层,通过凹槽限位,道床板为长6.5 m的标准板,宽2.8 m,厚260 mm,采用C40混凝土;道床板之间设置100 mm的板缝,底座板与道床板等长等宽,厚度为210 mm[8]。
两侧隧道内道床板采用纵向连续的钢筋混凝土结构,道床板厚度、材料与桥上相同。道床板下即为隧道支撑结构,道床板与隧道支撑结构竖向刚度取1×106kN/mm,采用线性弹性连接模拟;纵向刚度取300 kN/mm[6],采用非线性弹性连接模拟。
道床板与底座板摩擦阻力为0.91 kN/mm,采用非线性弹性连接模拟;限位凹槽橡胶垫板刚度为180 kN/mm[6],道床板与底座板竖向刚度取1×106kN/mm,采用线性弹性连接模拟。
主拱圈采用C50混凝土,拱上结构与桥台基础均为C35混凝土。
计算钢轨伸缩应力时不考虑梁升降温的交替变化,不考虑温度梯度,计算桥梁整体升温30 ℃[9];计算钢轨制动力时,轮轨黏着系数取0.164;制动力与挠曲力加载均只考虑满跨布载,单线加载[10],且只考虑制动力与挠曲力单独作用。
2 拱桥上无砟轨道纵向力
本节中计算了拱桥上钢轨伸缩力、挠曲力和制动力,其中伸缩力工况为全桥升温30 ℃;挠曲力工况为全桥满布ZK静活载;制动力工况为单线全桥满布。且计算结果中的轨道坐标−100.98~−0.98 m代表桥梁成都侧隧道,−0.88~52.88 m代表拱桥,52.98~152.98 m代表桥梁西安侧隧道,图中坐标0点为计算拱轴线左端拱脚处。
2.1 伸缩力
桥梁整体升温30 ℃计算钢轨应力,见图2。
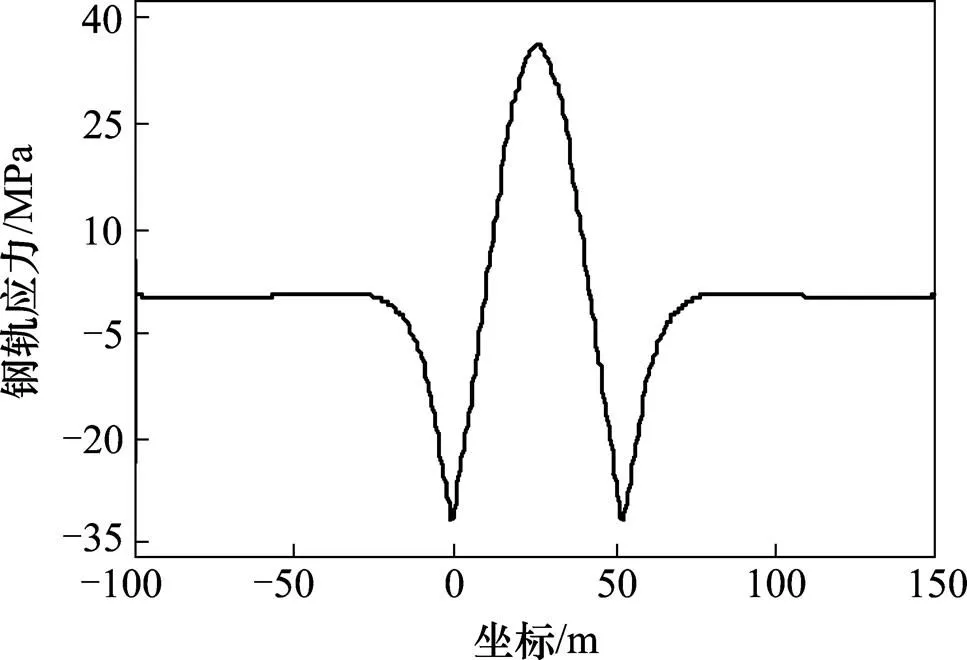
图2 钢轨伸缩力图
由图2可知,整体升温作用下由于桥体混凝土用量大,故拱顶上拱位移较大,引起钢轨较大拉应力,为36.5 MPa;最大压应力出现在拱桥两端,为31.9 MPa。可知,温度作用下,钢轨跨中与梁端受力较不利。
2.2 挠曲力
计算钢轨挠曲应力,见图3。在满跨ZK活载作用下钢轨应力较小,且跨中压应力大于梁端拉应力,跨中最大压应力为0.2 MPa,桥梁两端最大拉应力不足0.1 MPa。
2.3 制动力
采用单线制动,此桥设计荷载采用ZK活载,制动力计算中,轮轨黏着系数取0.164,荷载等效为均布荷载,加载于钢轨单元上计算钢轨制动应力,结果见图4。

图3 钢轨挠曲应力图

图4 钢轨制动应力图
由图4可知,在单线全桥满布荷载下,列车制动力最大应力出现在拱桥两端与隧道连接处,大小为4.0 MPa。
由于本桥为实腹式钢筋混凝土拱桥,混凝土用量大,因此成桥后桥梁刚度大,挠曲应力与制动应力较小,对结构影响不大。因此重点选取相邻隧道遮挡作用对伸缩力的影响、主拱圈分层施工条件下收缩徐变引起的钢轨纵向力。
3 相邻隧道遮挡作用的影响
本桥位于秦岭深处的V型河谷地段,海拔1 km以上,昼夜温差较大。桥隧过渡段拱桥两端的隧道结构较长,由于隧道对道床板及钢轨具有遮挡作用,隧道内外道床板和钢轨存在纵向温差。
文献[11]通过对风火山隧道内外温差进行为期1 a的监测得出:夏季隧道内外最大钢轨温差为40 ℃,最大气温温差为15 ℃,轨温最大变化梯度为0.8 ℃/m。结合既有研究[11−12],本文取夏季隧道内外钢轨最大温差40 ℃,道床板最大温差20 ℃,隧道过渡段温度最大变化梯度为0.8 ℃/m,计算隧道内外钢轨温差与道床板温差对钢轨应力影响。
3.1 道床板温差影响
计算道床板温差在5,10和20 ℃下钢轨应力与位移,与无温差(整体升温30 ℃)下钢轨应力与纵向位移进行对比,见图5。

(a) 钢轨应力;(b) 钢轨纵向位移
由图5可知,与无温差的钢轨最大拉应力36.5 MPa相比,温差在5,10和20 ℃情况下跨中钢轨最大拉应力分别为36.9,37.5和38.5 MPa,钢轨应力分别增大了1.0%,2.7%和5.5%。
与无温差的钢轨最大纵向位移1.83 mm相比,温差在5,0和20 ℃度情况下钢轨最大纵向位移分别为1.88,1.98和2.10 m,钢轨纵向位移分别增大了2.7%,8.1%和14.8%。
内外道床板温差作用下,道床板升温不同步,使钢轨产生了附加力,温差越大,附加力就越大。本文中钢轨应力在隧道内外道床板不同温差作用下产生的应力最大增幅5.5%,钢轨纵向位移最大增幅14.8%,对比可知道床板温差对钢轨有较明显的影响。
3.2 钢轨温差影响
将当地最高轨温取为60[8],计算钢轨纵向温差40,30,20和10 ℃情况下钢轨应力与纵向位移,见图6。
由图6可知,不同温差钢轨应力关于桥梁跨中对称分布,由两侧隧道向桥梁跨中逐渐增大。在无钢轨温差条件下,钢轨应力为145.9 MPa,在温差40,30,20和10 ℃条件下,隧道内钢轨最小应力分别为49.3,70.1,97.3和122.2 MPa,钢轨纵向位移最大值分别为1.20,1.08,0.89和0.56 mm。

(a) 钢轨应力;(b) 钢轨纵向位移
钢轨纵向温差条件下,钢轨应力有较大差别,隧道内钢轨温度变化小,桥上钢轨温差大,因此在钢轨中产生了温度力。钢轨最大纵向位移为1.2 mm,钢轨纵向位移最大值随着温差的降低逐渐由隧道向桥梁两端靠近。
4 主拱圈分层施工的影响
混凝土的收缩徐变对拱桥后期线形和钢轨应力有较大影响,本节采用《铁路桥涵钢筋混凝土和预应力混凝土结构设计规范》(以下简称“铁路桥规”)(TB 10002.3—2005)进行计算。木河中桥最初设计为一次浇筑主拱圈,而后考虑到施工难度与施工周期,充分利用已有的工器具装备,提高施工安全储备进行了施工变更,修改为分层浇筑主拱圈,将主拱圈分为2层,第1层高1.3 m,第2层高1.2 m。不同的主拱圈施工方法,使得主拱圈混凝土龄期不同,施工时间不同,影响拱桥后期收缩徐变的发生,进而对钢轨应力产生影响。因此,有必要探究主拱圈一次浇筑和分层浇筑不同情况下钢轨铺设后60 d到10 a时间内混凝土的收缩徐变对钢轨应力的影响,并对比不同规范收缩徐模型对钢轨纵向力的影响[13]。
4.1 分层施工影响
模拟拱桥施工阶段,取成桥后120 d铺轨,对主拱圈不同施工方法进行比较,结果见图7。

(a) 钢轨应力;(b) 钢轨纵向位移
图7可知,以分层施工为例,钢轨应力与纵向位移在铺轨后不断增长,但增长速率不断减慢,1 a之内发展最快。如果以10 a为最终状态,对比3 a与10 a的收缩徐变,钢轨拉应力由20.3 MPa增加到21.9 MPa,增加了7%,钢轨压应力由19.8 MPa增加到21.8 MPa,增加了9.1%,说明3 a以后其收缩徐变基本完成。钢轨最大压应力与钢轨最大拉应力相差较小;由于拉压应力总体变化规律相似,故以下对压应力做出分析。
由表1可知,主拱圈一次浇筑钢轨增加的应力分别为本阶段分层浇筑的270.0%,63.5%,23.2%和20.6%,对相同阶段钢轨纵向位移而言一次浇筑的位移增量分别为本阶段分层浇筑的271.4%,64.7%,23.5%和14.9%。
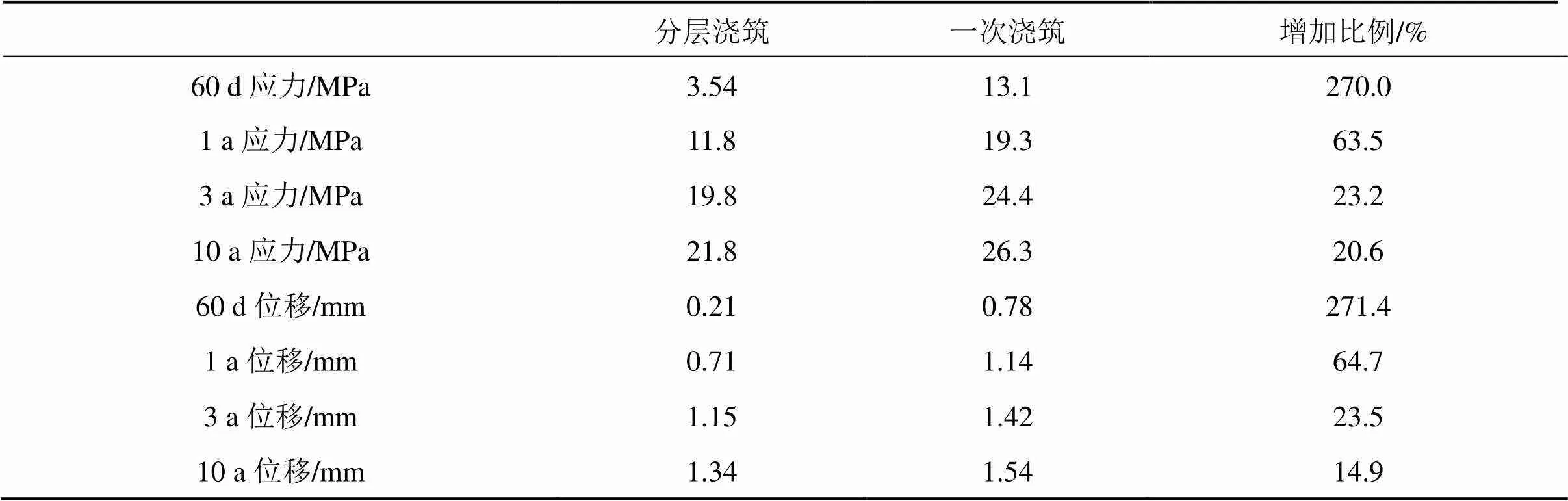
表1 主拱圈不同施工方法钢轨应力位移最值统计
每个收缩徐变阶段分层施工与一次浇筑钢轨应力位移都有所差别。在10 a的收缩徐变情况下,分层浇筑钢轨压应力为21.8 MPa,与一次浇筑相比降低了20.6%;分层施工的钢轨纵向位移为1.34 mm,与一次浇筑的1.54 mm相比缩小了14.9%。
从钢轨应力与纵向位移的变化可知,由于主拱圈进行分层浇筑,先浇筑的一层主拱圈先开始收缩徐变,相比一次浇筑而言,分层浇筑的混凝土收缩徐变先发生,且分层浇筑工期较长,收缩徐变在铺轨前发生较多,因此分层浇筑对铺轨后钢轨的应力位移影响相对较小。
4.2 不同规范收缩徐变差别
以主拱圈分层浇筑为例,计算《铁路桥规》[14]与《欧洲规范》[15]中不同收缩徐变模型在铺轨后60 d到10 a钢轨应力与位移的变化,见图8。
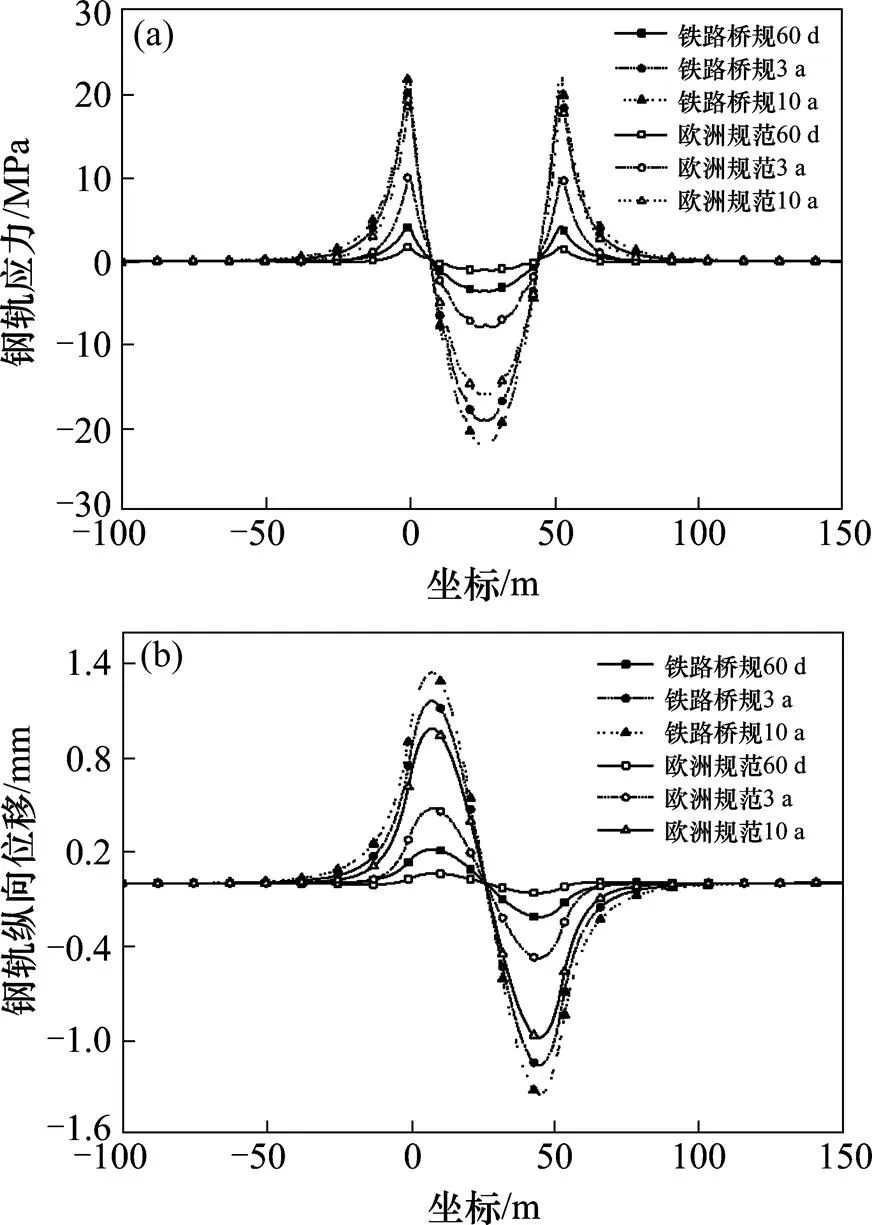
(a) 钢轨应力;(b) 钢轨纵向位移
由图8可知,《欧洲规范》中收缩徐变效应在60 d,3 a和10 a对应的钢轨压应力分别为1.7,10.0和18.4 MPa,钢轨纵向位移分别为0.06,0.47和0.98 mm。
《铁路桥规》计算的收缩徐变在规律上与《欧洲规范》一致,应力与纵向位移不断增长,而增长速率逐渐减小,但其在计算数值上较《欧洲规范》大;《铁路桥规》在铺轨的3 a内收缩徐变发生迅速,以10 a的状态作为参考,3 a的收缩徐变已达到90%以上;而《欧洲规范》3 a的收缩徐变只完成了54.3%;《铁路桥规》10 a收缩徐变情况下最终钢轨最大压应力为21.9 MPa,而《欧洲规范》10 a收缩徐变情况下钢轨最大压应力为18.4 MPa,最大值为《铁路桥规》的80%左右。
5 结论
1) 对本桥而言,由于竖向刚度较大,列车竖向荷载及制动作用引起的钢轨应力均较小。伸缩力成为主要控制性荷载,其最大值出现在跨中为 36.5 MPa。
2) 考虑相邻隧道的遮挡作用后,钢轨和道床板将出现纵向温度差值。钢轨应力和纵向位移随道床板和钢轨纵向温差的增大而增大,其中纵向温差对钢轨应力影响显著。当钢轨温差为40 ℃时,应力差值达94.5 MPa,钢轨纵向位移达1.20 mm,因此隧道遮挡对钢轨温度应力影响较大,在设计中应予以考虑。
3) 客运专线RC实腹式拱桥施工过程中可优先考虑主拱圈分层施工以减小收缩徐变对钢轨应力变形的影响。与《欧洲规范》相比,《铁路桥规》考虑10 a收缩徐变情况下,钢轨最终压应力较大,而且应力发展速度也较快。
[1] XU Qingyuan, ZHOU Xiaolin, ZENG Zhiping, et al. Mechanics model of additional longitudinal force transmission between bridges and continuously welded rails with small resistance fasteners[J]. Journal of Central South University of Technology, 2004, 11(3): 336−339.
[2] YAN Bin, DAI Gonglian. Longitudinal forces of continuously welded rail on high-speed railway cable-stayed bridge considering impact of adjacent bridges[J]. Journal of Central South University, 2012. 19(8): 2348−2353.
[3] 于向东, 尹兴权, 闫斌. 相邻桥跨对大跨钢桁梁桥-轨道系统的影响[J]. 华南理工大学学报(自然科学版), 2016, 44(6): 137−142. YU Xiangdong, YIN Xingquan, YAN Bin. Influence of adjacent bridge on interaction system of large-span steel truss girder and railway[J]. Journal of South China University of Technology, 2016, 44(6): 137−142.
[4] YAN Bin, DAI Gonglian, ZHANG Huaping. Beam-track interaction of high-speed railway bridge with ballast track [J]. Journal of Central South University, 2012, 19(5): 1447−1453.
[5] SONG M K, NOH H C. CHOI C K. A new three-dimensional finite element analysis model of high-speed train–bridge interactions[J]. Engineering Structures, 2004, 26(11): 1659−1660.
[6] 曲村, 高亮, 乔神路. 高速铁路长大桥梁CRTS Ⅰ型双块式无砟轨道无缝线路影响因素分析[J]. 铁道工程学报, 2011, 28(3): 46−51. QU Cun, GAO Liang, QIAO Shenlu. Analysis of influence factors on CRTS I double-block ballastless track CWR on long-pan bridge of high-speed railway[J]. Journal of Railway Engineering Society, 2011, 28(3): 46−51.
[7] 徐庆元, 陈秀方, 周小林, 等. 高速铁路桥上无缝线路力学计算模型对比[J]. 交通运输工程学报, 2005, 5(3): 19−24. XU Qingyuan, CHEN Xiufang, ZHOU Xiaolin, et al. Mechanics computation model comparison of continuously welded rails on high speed railway bridges [J]. Journal of Traffic and Transportation Engineering, 2005, 5(3): 19−24.
[8] TB 10015—2012, 铁路无缝线路设计规范[S]. TB10015—2012, Code for design of railway continuous welded rail[S].
[9] Ruge P, Birk C. Longitudinal forces in continuously welded rails on bridge decks due to nonlinear track-bridge interaction[J]. Computers and Structures, 2003, 81(22): 2219−2236.
[10] CHEN Rong, WANG Ping, WEI Xiankui. Track-bridge longitudinal interaction of continuous welded rails on arch bridge[J]. Mathematical Problems in Engineering, 2013, 2013(3): 237−245.
[11] 张向民, 高亮, 曾志平. 青藏铁路风火山隧道气温轨温试验及无缝线路设计[J]. 北京交通大学学报, 2013, 37(3): 73−78. ZHANG Xiangmin, GAO Liang, ZENG Zhiping. Experiment of air and rail temperature and design CWR track of Fenghuo mountain tunnel on Qinghai-Tibet railway[J]. Journal of Beijing Jiaotong University, 2013, 37(3): 73−78.
[12] 吴海彬. 寒区特长公路隧道积水冻胀问题和隧道内温度场分布规律研究[D]. 成都: 西南交通大学, 2015. WU Haibin. A research on frost heave force and temperature field inside long road tunnels in cold area[D]. Chengdu: Southwest Jiaotong University, 2015.
[13] 刘从新. 考虑收缩徐变影响的斜拉桥梁轨相互作用研究[D]. 长沙: 中南大学, 2012. LIU Congxin. Research on track-bridge interaction of cable-stayed bridge considering influence of the shrinkage and creep[D]. Changsha: Central South University, 2012.
[14] TB 10002.3−2005, 铁路桥涵钢筋混凝土和预应力混凝土结构设计规范[S]. TB 10002.3−2005, Code for design on reinforced and prestressed concrete structure of railway bridge and culvert[S].
[15] Eurocode 2: Design of concrete structures-Part 1-1: General rules and rules for building[S].
(编辑 涂鹏)
Continuously welded rail track longitudinal forces distribution characteristics of solid web reinforced concrete arch bridge of bridge-tunnel connection section
YU Xiangdong1, LI Yukun2, YAN Bin1
(1. School of Civil Engineering, Central South University, Changsha 410075, China; 2. Hunan Provincial Communications Planning, Survey & Design Institute Co., Ltd, Changsha 410008, China)
A rail-slab-solid web RC arch bridge finite element model was established under the background of a 52m solid web reinforced concrete arch bridge with CRTS I double-block ballastless track of high-speed railway from Xi’an to Chengdu. Longitudinal forces of ballastless track was analyzed. On this foundation, longitudinal force of continuously welded rail track which was created by temperature variations of rail and slab due to tunnel shield was explored. And the influence of shrinkage and creep of the longitudinal force of rail in different construction methods of arch ring was discussed. The results show that the maximum value of the expansion force appears in the mid-span, and the value is large, which is the dominant load. Tunnel shield has remarkable influence on rail stress. Under the temperature variations of slab, the rail stress increases 1.0%~5.5%, and the maximum longitudinal displacement of the rail increases 14.8%. Rail stress and longitudinal displacement under the temperature variations of rail are heavy, which should be taken into account in design. Considering the influence of shrinkage and creep of concrete for 10 years, constructing layer by layer can reduce the rail compressive stress by 20.6% and the longitudinal displacement of the rail by 14.9% compared with one-time pouring.
solid web reinforced concrete arch bridge; continuously welded rail track; longitudinal force of rail; bridge-tunnel connection section; shrinkage and creep
10.19713/j.cnki.43−1423/u.2018.12.007
U213.912
A
1672 − 7029(2018)12 − 3066 − 07
2017−11−15
国家重点研发计划资助项目(2017YFB1201204)
于向东(1970−),男,河南遂平人,副教授,博士,从事桥梁抗风及梁轨相互作用研究;E−mail:xdyu@csu.edu.cn
