基于泊松−威布尔过程的钢轨修理周期预测研究

白文飞，张伟，刘仍奎，王福田，孙全欣



基于泊松−威布尔过程的钢轨修理周期预测研究

白文飞1, 2，张伟3，刘仍奎1，王福田1，孙全欣4

(1. 北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044； 2. 北京城建设计发展集团股份有限公司 城市轨道交通绿色与安全建造国家工程实验室，北京 100037； 3. 北京市交通委员会，北京 100073； 4. 北京交通大学 交通运输学院，北京 100044)

在将线路上连续的钢轨离散划分成多个钢轨单元的基础上，提出基于泊松-威布尔过程的钢轨修理周期预测模型。模型以单个钢轨单元为研究对象，在充分考虑不同空间位置钢轨单元劣化过程异质性的前提下，根据钢轨单元伤损的历史检测数据，对每个钢轨单元的维修周期和大修周期进行了预测，利用北京地铁2号线钢轨的伤损检测数据对模型的有效性进行验证。研究结果表明：本文提出的钢轨修理周期预测模型能够为管理者合理安排钢轨的修理计划提供足够的决策支持，辅助管理者实现钢轨的“预防修”。

钢轨；维修周期；大修周期；劣化；异质性；泊松−威布尔过程

钢轨是列车运行的基础，在机车车辆动荷载的反复作用下，钢轨的状态不断劣化，线路管理者需要持续不断地对钢轨进行修理(包括维修和大修)，以保证行车安全。目前我国铁路钢轨修理主要采取“故障修”和“周期修”的模式[1]，即依据钢轨出现的伤损类型和伤损等级选取相应的修理方式或依据钢轨的累计通过总重周期性地进行修理，此种模式缺少对钢轨状态的预测，难以依据钢轨劣化规律实现钢轨的“预防修”。因此，研究钢轨状态劣化规律，准确预测钢轨修理周期，对线路管理者合理安排钢轨修理计划，实现科学控制修理成本和保障行车安全具有十分重要的意义。对于钢轨劣化规律及修理周期预测的研究，国内外学者做了大量工作，主要分为2类：第1类是从钢轨病害发展机理分析的角度进行研究。Romano等[2]基于半概率方法建立了钢轨的剩余寿命评估模型，以铝热焊钢轨焊接接头轨底表面裂纹为分析对象，计算了每天钢轨焊接接头失效的概率；Mai等[3]基于eXtended Finite Element Method (XFEM)建立了钢轨疲劳裂纹发展的数值仿真模型，该模型的结果表明疲劳裂纹面的摩擦系数越小裂纹发展得越快，裂纹与轨枕之间的相对位置(在轨枕上方或处于2根轨枕之间)对疲劳裂纹的发展没有显著影响。刘亮等[4]利用断裂力学理论建立了高速铁路钢轨剩余寿命的预测模型，模型基于钢轨的疲劳裂纹扩展率估计了钢轨的疲劳剩余寿命；周宇等[5]将基于Archard磨耗理论的钢轨型面磨耗预测模型和基于临界平面法的钢轨疲劳裂纹萌生寿命预测模型结合起来，提出了考虑磨耗的裂纹萌生寿命预测方法，预测了钢轨在磨耗影响下的裂纹萌生特征；许玉德等[6]基于车辆−轨道动力学仿真、轮轨非Hertz滚动接触模型和钢轨材料磨损模型建立了钢轨磨耗预测模型，对铁路曲线段钢轨磨耗进行了预测。上述基于钢轨病害发展机理进行的研究主要是针对某一类钢轨病害的劣化进行分析，例如疲劳裂纹和钢轨磨耗等，但对于一段钢轨的综合状态和使用寿命，如1 km钢轨，由于受到多种病害的影响，无法直接应用上述研究成果去进行评定和分析。第2类是从钢轨失效统计分析的角度进行研究。Schafer II等[7]基于统计逻辑回归模型建立了钢轨折断预测模型，对钢轨的使用年限、类型、位置和维修历史等28类因素对钢轨折断的影响程度进行了分析，并对线路上最有可能发生钢轨折断的位置进行了预测；Chattopadhyay 等[8]在分析各类钢轨病害劣化过程及影响钢轨折断的各种因素的基础上构建钢轨折断预测模型，对每个钢轨区段某个时刻发生断轨的概率以及线路上一段时间内发生断轨次数进行预测；Veskovic等[9]基于模糊逻辑理论，以轨温、使用年限、通过总重和曲度4个因素为输入变量，建立了断轨频率预测模型，对某一线路区间1个月内的断轨数量进行了预测。颜秉善[10]基于威布尔分布建立了钢轨疲劳失效概率和运量之间的关系，对不同长度线路区段上钢轨的剩余寿命、大修周期和可靠度进行了预测；习年生等[11]同样基于威布尔分布对铁路直线区段钢轨疲劳重伤率分布规律进行了分析，并对钢轨的疲劳寿命进行了预测。上述基于钢轨失效统计分析进行的研究主要针对的是较大范围内路网上某个时刻发生钢轨重伤或折断概率的预测或者该范围内钢轨使用寿命的统计规律。但由于钢轨状态的劣化受设计、建设、运营和自然环境等多种因素的综合影响，不同空间位置上各类因素的影响程度不同，使不同空间位置上钢轨的劣化过程呈现出异质 性[12]，包括劣化速度、使用寿命和修理周期等均不一致。上述方法忽略了不同位置钢轨劣化过程的异质性，难以实现对不同特定空间位置上钢轨使用寿命和修理周期的精细化估计。本文基于以往研究存在的局限性，提出将线路上连续的钢轨划分成一定长度的钢轨单元，在充分考虑钢轨劣化过程异质性的条件下，利用钢轨伤损历史检测数据，建立基于泊松−威布尔过程的钢轨修理周期预测模型个性化预测每个钢轨单元的维修周期和大修周期，为合理安排钢轨修理计划提供决策支持。

1 基于泊松−威布尔过程的钢轨修理周期预测模型

1.1 钢轨单元的划分与状态评定

对于钢轨的修理管理，很多国家都以每公里钢轨伤损数量作为判定是否需要对其进行修理的依据[11, 13]，我国的《铁路线路修理规则》[1]规定，钢轨累计疲劳重伤平均达到2~4根/km时，应安排线路大修。因此，为减少钢轨劣化过程异质性对准确把握钢轨使用寿命的影响，论文采用1 km长度将线路上连续的钢轨划分成多个钢轨单元，并选取钢轨单元内的累计重伤或折断次数来评定钢轨单元的状态，在此基础上个性化研究每个钢轨单元的钢轨修理周期，包括钢轨单元的维修周期和大修周期，钢轨单元划分示意图如图1所示。

图1 钢轨单元划分示意图

本研究中的钢轨单元维修是指当钢轨单元内出现钢轨重伤或折断时，更换重伤或折断的钢轨；维修周期是指钢轨单元刚投入使用或最近一次完成大修的时刻到首次发生重伤或折断时刻之间的时间间隔，以及相邻2次重伤或折断时刻之间的时间间隔。

钢轨单元大修是指当钢轨单元内的累计重伤或折断次数达到阈值时，应更换整个钢轨单元内的钢轨，其中不同类型、不同速度等级的线路上钢轨单元的大修阈值不一致，应根据实际管理要求设定；大修周期是指钢轨单元刚投入使用或最近一次完成大修换轨的时刻到发生第次钢轨重伤或折断的时刻之间的时间间隔。

1.2 钢轨单元维修和大修周期预测模型

基于上一节中对钢轨单元的划分，本文利用泊松−威布尔过程方法建立钢轨单元的修理周期预测模型，模型以每个钢轨单元为研究对象，充分考虑不同钢轨单元劣化过程的异质性，利用每个钢轨单元自己的伤损历史检测数据个性化预测每个钢轨单元的维修和大修周期。

1.2.1 泊松-威布尔过程

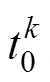
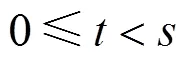
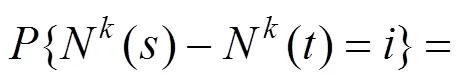
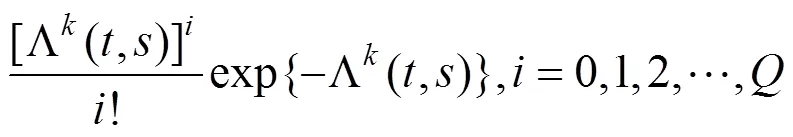
式中：

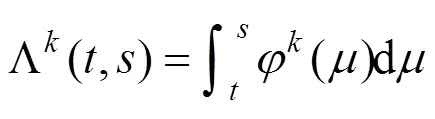
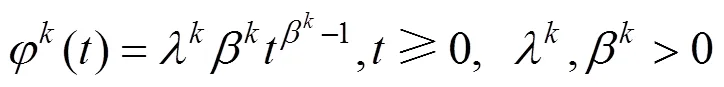
1.2.2 钢轨单元维修周期预测

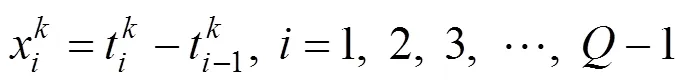
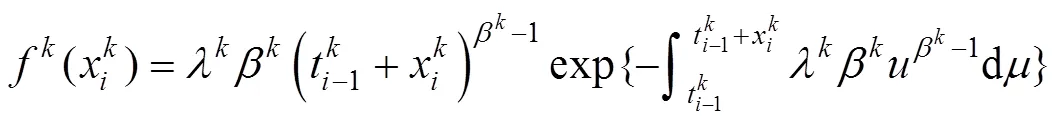
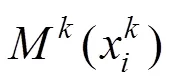
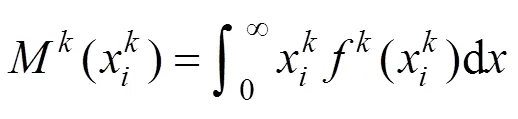
1.2.3 钢轨单元大修周期预测

1.3 模型参数估计

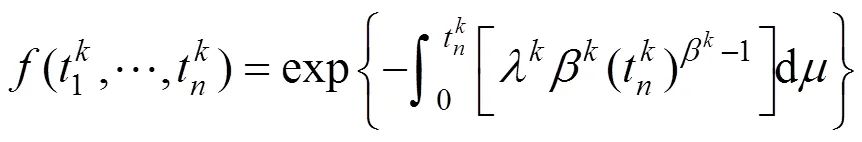
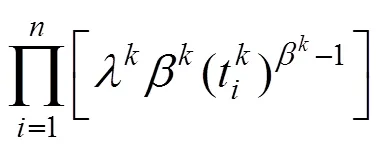
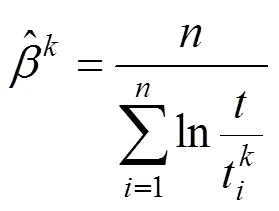
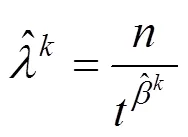
随着的不断推移，当有新的检测数据时，根据上述似然函数，模型可自适应地调整每个钢轨单元的参数，优化模型估计精度。一般来说，为了保证模型的应用效果，至少需要一个修理周期内的检测数据。

2 实证分析

北京地铁2号线全长23.1 km，正线采用50 kg/m的钢轨，上下2个行车线路共有136条曲线，约占线路总长的31.6%，其中半径小于等于600 m的有31条，占曲线总数量的22.8%。论文利用北京地铁2号线2008年1月到2017年3月发生过重伤或折断的42个钢轨单元的伤损检测记录，对本文提出的模型进行实例验证，其中伤损检测记录包括钢轨磨耗记录和疲劳伤损记录，共计1 063条，重伤检测记录共计124条，具体如表1所示。根据北京地铁钢轨的实际管理情况，本文设定北京地铁钢轨单元内的累计重伤或折断次数达到3次时，即=3，应安排钢轨单元的大修换轨。

2.1 维修周期预测结果与误差分析

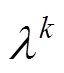
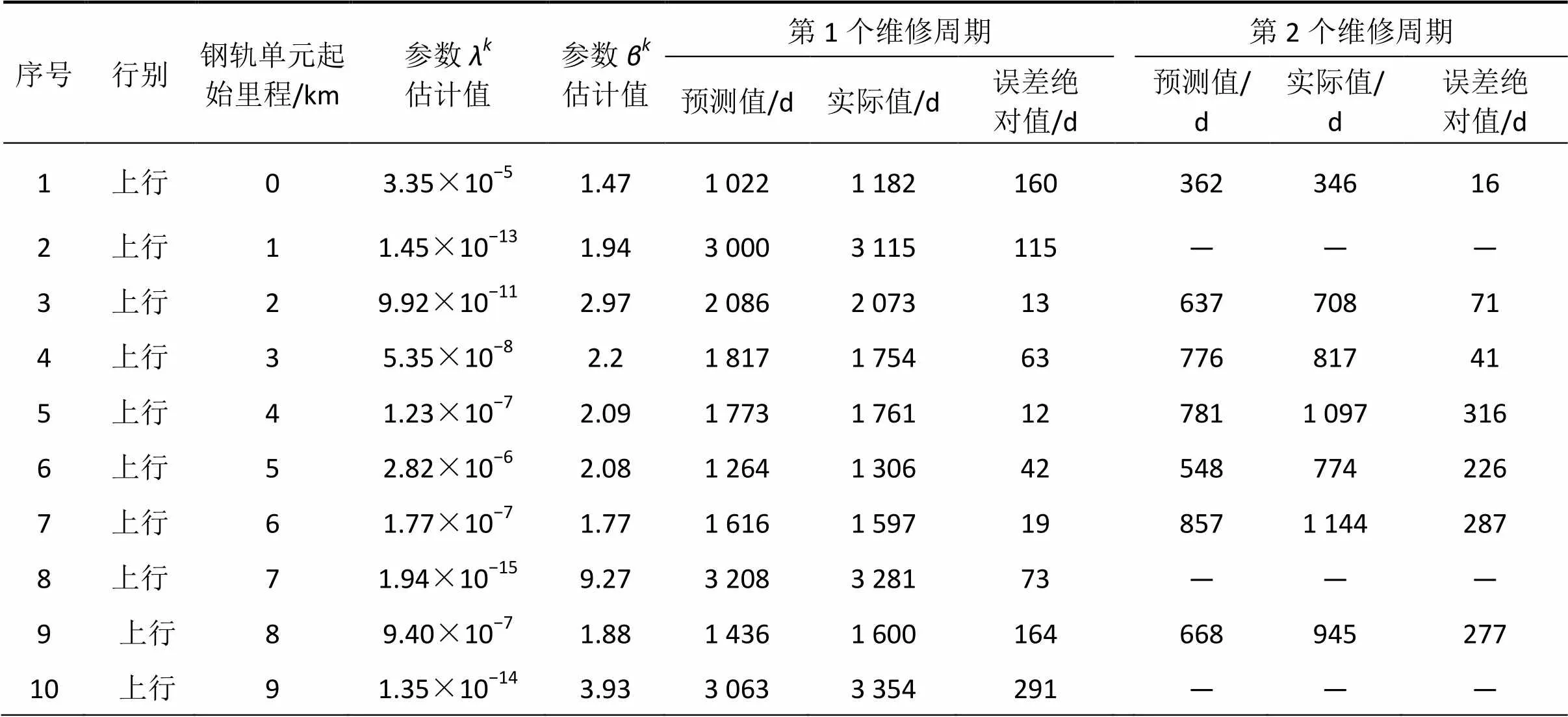
从表2中可以看到，不同钢轨单元的参数和的估计结果不同，反映出不同钢轨单元劣化过程的异质性，表现为不同钢轨单元维修周期的预测结果不同。表中序号1，6，12，20，22，27，33和42等8个钢轨单元维修周期预测结果相对于其他钢轨单元的维修周期预测结果较短，通过对比2号线线路设备数据，这8个钢轨单元内小半径曲线较多，受曲线磨耗影响劣化速度较快，通过对比上述钢轨单元的实际维修周期结果，预测结果反映的情况与实际结果相一致；表中序号2，8，10，15，23，29，31和36等8个钢轨单元维修周期预测结果相对于其他钢轨单元的维修周期预测结果较长，通过对比2号线线路设备数据，这8个钢轨单元均位于直线区段或大半径曲线区段上，受磨耗影响较小，劣化速度较慢，通过对比上述钢轨单元的实际维修周期结果，预测结果反映的情况也与实际结果相一致。

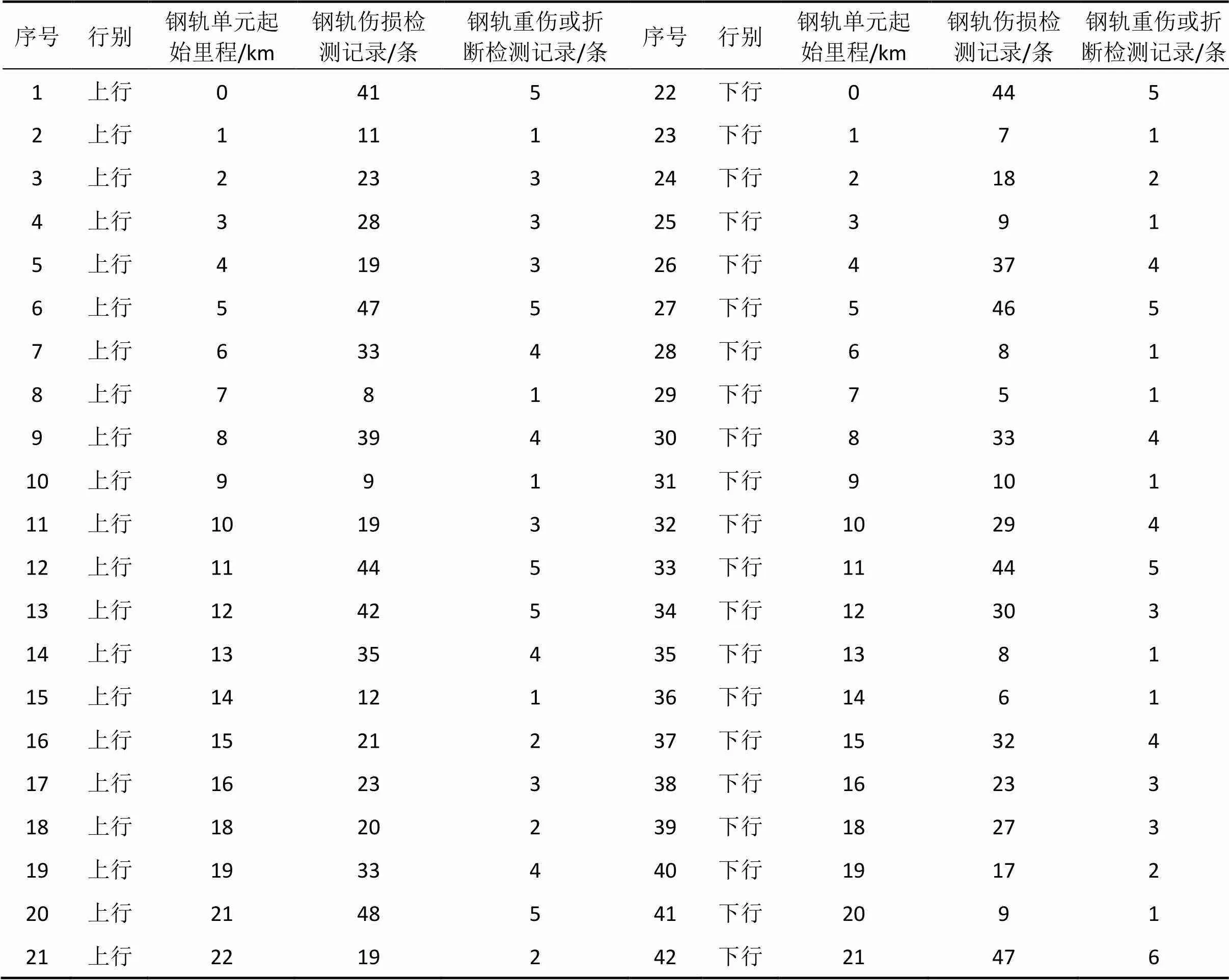
表1 北京地铁2号线2008年1月到2017年3月的钢轨伤损检测记录统计结果

表2 北京地铁2号线钢轨单元维修周期预测结果

Table 2 Predicted maintenance periods of rail segments on Beijing Metro Line 2

序号行别钢轨单元起始里程/km参数λk估计值参数βk估计值第1个维修周期第2个维修周期 预测值/d实际值/d误差绝对值/d预测值/d实际值/d误差绝对值/d 1上行03.35×10−51.471 0221 18216036234616 2上行11.45×10−131.943 0003 115115——— 3上行29.92×10−112.972 0862 0731363770871 4上行35.35×10−82.21 8171 7546377681741 5上行41.23×10−72.091 7731 761127811 097316 6上行52.82×10−62.081 2641 30642548774226 7上行61.77×10−71.771 6161 597198571 144287 8上行71.94×10−159.273 2083 28173——— 9 上行89.40×10−71.881 4361 600164668945277 10 上行91.35×10−143.933 0633 354291———

表3 北京地铁2号线钢轨单元维修周期预测结果误差分布

为了分析模型的预测精度，本文将上述预测结果与实际维修周期进行对比，并统计了预测结果的误差分布，具体如表3所示。

从表3中可以看到，对于钢轨单元维修周期，所有钢轨单元的预测结果误差均小于1 a，并且有68.06%的预测结果误差不大于半年。根据《北京地铁工务维修规则》[14]，对于钢轨疲劳伤损，采用超声波检测和人工检测相结合的方式，每2个月进行1次检测；对于曲线钢轨磨耗，采用人工定点测量的方式，每季度测量进行1次，当发现钢轨轻伤时，会适当提高检测频率。随着检测数据的积累和更新，模型的计算精度也会进一步提高，模型可以较为准确地预测维修周期，有助于线路管理者及时合理安排钢轨维修计划，在钢轨重伤或折断发生之前及时将其更换，保障行车安全。其中对于维修周期预测结果误差绝对值相对较大的钢轨单元，从表1中该钢轨单元的伤损记录统计结果可以看到，其伤损检测记录较少，导致模型结果误差相对较大，随着伤损检测记录的增加，估计结果的精度也会逐步提高。

2.2 大修周期预测结果与误差分析

根据北京地铁2号线钢轨伤损的检测记录，利用提出的大修周期预测模型计算了钢轨单元的大修周期。同样以下行K4+000~K5+000这一钢轨单元为例，将求得的参数和的估计结果代入1.2.3节的式(8)求得该钢轨单元的大修周期估计结果为2 606 d。截止到2017年3月已累计发生过3次重伤或折断的全部25个钢轨单元的大修周期的估计结果如表4所示。

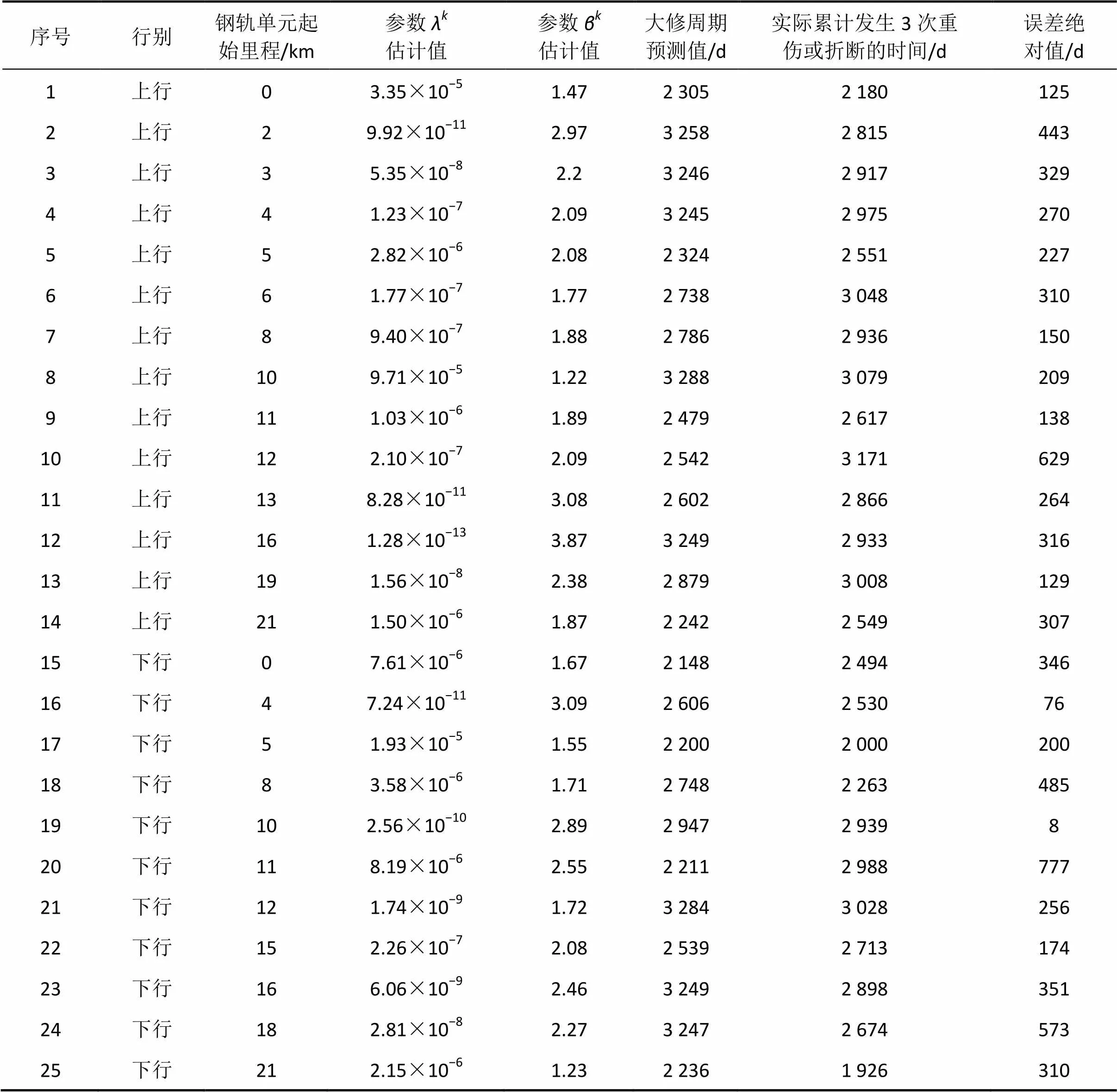
表4 选取的北京地铁2号线钢轨单元大修周期预测结果

表4中不同钢轨单元的参数和的估计结果不同，反映出不同钢轨单元劣化过程的异质性，表现为不同钢轨单元大修周期的预测结果也不同。表中序号1，5，9，14，15，17，20和25等钢轨单元由于受小半径曲线磨耗影响劣化速度较快，大修周期较短，预测结果与实际情况相一致。

为了分析大修周期的预测精度，将上述预测结果与实际累计发生3次重伤或折断的时间进行了对比，并统计了预测结果的误差分布，如表5所示。

表5 北京地铁2号线钢轨单元大修周期预测结果误差分布

从表5中可以看到，对于大修周期，28.00%的预测结果误差小于半年，52.00%的预测结果误差大于半年小于等于1 a，总计80.00%的预测结果误差小于1 a。根据《北京地铁工务维修规则》[14]，线路管理者需提前1 a安排钢轨的大修计划，因此本文提出的钢轨大修周期预测模型的计算精度能够满足钢轨大修管理的需要，可为管理者合理安排钢轨大修计划，科学配置修理资源提供决策支持，更好地实现钢轨的“预防修”。其中对于大修周期预测结果误差绝对值相对较大的钢轨单元，从表1中该钢轨单元的伤损统计结果看到，同样是由于伤损检测记录较少，导致模型结果误差相对较大，随着伤损检测记录的增加，其大修周期估计结果的精度也会逐步提高。

3 结论

1) 为充分考虑不同空间位置上钢轨劣化过程异质性，本研究以1 km长度将线路连续的钢轨划分成了多个钢轨单元，以每个钢轨单元为研究对象进行个性化分析。

2) 利用泊松−威布尔过程方法构建了钢轨修理周期预测模型，根据钢轨单元伤损的历史检测数据，模型能够对每个钢轨单元的维修周期和大修周期进行精细化预测。

3) 以北京地铁2号线钢轨伤损的实际检测数据，预测了2号线钢轨单元的维修周期和大修周期，对本文提出的模型进行了验证。结果表明本文提出的钢轨修理周期预测模型能够为管理者合理安排钢轨的维修和大修计划提供足够的决策支持，并且能够解决原有钢轨修理模式中存在的缺少根据钢轨状态数据对钢轨周期的合理估计和对钢轨劣化过程异质性考虑不足的问题，适用于各种类型钢轨的修理周期预测，更好地辅助管理者实现钢轨的“精细修”、“精确修”和“预防修”。

4) 随着钢轨伤损历史数据不断积累，本模型的估计精度还会进一步得到改善。在未来的研究中，将进一步在本文研究成果的基础上优化编制钢轨修理计划，在保证钢轨状态满足管理要求的前提下使钢轨的修理成本最优。

[1] 中华人民共和国铁道部. 铁路线路修理规则[M]. 北京:中国铁道出版社, 2010: 90−91. The Railway Ministry of People’s Republic of China. Rules of railway track maintenance[M]. Beijing: China Railway Press, 2010: 90−91.

[2] Romano S, Manenti D, Beretta S, et al. Semi- probabilistic method for residual lifetime of aluminothermic welded rails with foot cracks[J]. Theoretical and Applied Fracture Mechanics, 2016, 85(85): 398−411.

[3] Mai S H, Gravouil A, Nguyen-Tajan M L, et al. Numerical simulation of rolling contact fatigue crack growth in rails with the rail bending and the frictional contact[J]. Engineering Fracture Mechanics, 2017, 174: 196−206.

[4] 刘亮, 王文健, 郭俊, 等. 高速铁路钢轨剩余疲劳寿命预测研究[J]. 机械强度, 2012(4): 120−126. LIU Liang, WANG Wenjian, GUO Jun, et al. Prediction of residual fatigue life for high-speed railway rail[J]. Journal of Mechanical Strength, 2012(4): 120−126.

[5] 周宇, 张杰, 王少锋, 等. 考虑磨耗的钢轨疲劳裂纹萌生寿命预测仿真[J]. 铁道学报, 2016, 38(7): 91−97. ZHOU Yu, ZHANG Jie, WANG Shaofeng, et al. Simulation on rail head crack initiation life prediction considering rail wear[J]. Journal of the China Railway Society, 2016, 38(7): 91−97.

[6] 许玉德, 魏恺, 孙小辉, 等. 钢轨磨耗预测模型及其算法的优化[J]. 中国铁道科学, 2016, 37(4): 48−53. XU Yude, WEI Kai, SUN Xiaohui, et al. Prediction model and algorithm optimization for rail wear[J]. China Railway Science, 2016, 37(4): 48−53.

[7] Schafer II D, Barkan C. A prediction model for broken rails and an analysis of their economic impact[C]// Proceedings of the AREMA 2008 Annual Conference, Salt Lake City, Utah, United States, 2008: 1−32.

[8] Chattopadhyay G, Kumar S. Parameter estimation for rail degradation model[J]. International Journal of Performability Engineering, 2009, 5(2): 119−130.

[9] Vesković S, Tepić J, Ivić M, et al. Model for predicting the frequency of broken rails[J]. Metalurgija, 2012, 51(2): 221−224.

[10] 颜秉善. 钢轨伤损及换轨周期的预测[J]. 铁道学报, 1988, 10(10): 88−97. YAN Bingshan. Prediction rail damage and economic timing for its renewal[J]. Journal of the China Railway Society, 1988, 10(10): 88−97.

[11] 习年生, 周清跃. 钢轨的疲劳重伤率分布规律与疲劳寿命预测[J]. 中国铁道科学, 2004, 25(5): 53−56. XI Niansheng, ZHOU Qingyue. Distribution and predicyion of rail fatigue failures[J]. China Railway Science, 2004, 25(5): 53−56.

[12] BAI Lei, LIU Rengkui, WANG Feng, et al. Estimating railway rail service life: A rail-grid-based approach[J]. Transportation Research Part A: Policy and Practice, 2017, 105: 54−65.

[13] 徐爱民, 高亮, 袁昊. 北京地铁轨道结构大修周期研究[J]. 铁道标准设计, 2009(2): 25−29. XU Aimin, GAO Liang, YUAN Hao. Renewal period of track structure of Beijing Metro[J]. Railway Standard Design, 2009(2): 25−29.

[14] QB(J)BDY(A)XL003-2015, 北京地铁工务维修规则[S]. QB(J)BDY(A)XL003-2015, Beijing metro track maintenance rules[S].

(编辑 涂鹏)

Research on prediction for rail maintenance period based on Poisson-Weibull process

BAI Wenfei1, 2, ZHANG Wei3, LIU Rengkui1, WANG Futian1, SUN Quanxin4

(1. State Key Laboratory of Rail Traffic Control and Safety, Beijing Jiaotong University, Beijing 100044, China; 2. National Engineering Laboratory for Green & Safe Construction Technology in Urban Rail Transit, Beijing Urban Construction Design & Development Group Co. Ltd, Beijing 100037, China 3. Beijing Municipal Commission of Transport, Beijing 100073, China; 4. School of Traffic and Transportation, Beijing Jiaotong University, Beijing 100044, China)

In this paper, continuous rails on a line of track are divided into rail segments discretely and a prediction model based on the Poisson-Weibull process is proposed. In the proposed model, each single rail segment is regarded as a unit whose maintenance and renewal period are analyzed individually relying upon the history records of its rail defect detection, considering the heterogeneities in deterioration processes of rail segments in separate locations. Finally, the model is validated through a case study of the Beijing Metro, using inspection records of rail defects of Line 2. The model is found to show good agreement with the rail inspection and maintenance records of the Beijing Metro, indicating its appropriateness for use by railroad management in scheduling future rail maintenance plans and realizing the ‘preventive maintenance’ of the rails.

rail; maintenance period; renewal period; deterioration; heterogeneity; Poisson-Weibull process

10.19713/j.cnki.43−1423/u.2018.12.008

U216.42+4

A

1672 − 7029(2018)12 − 3073 − 09

2017−10−20

国家自然科学基金资助项目(51578057)；北京交通大学轨道交通控制与安全国家重点实验室自主研究项目(RCS2016ZT007)

白文飞(1991−)，男，山东临沂人，工程师，博士，从事轨道交通基础设施管理研究；E−mail：wfbai@bjtu.edu.cn