利用柯西不等式的变形解题

☉河南省驻马店高级中学 耿杉杉

文1把课本上的一类条件不等式的证明利用函数思想，先从不等式中抽象出一个函数，然后，利用该函数图像总是在对应点处的切线的上方或下方构造出新的不等式，最后对这些新不等式进行累加，从而使原不等式得证.这样证明不等式确实很巧妙.文2利用重要不等式的变形再次对这些不等式进行了证明，读后也让人耳目一新.通过这两篇文章的学习研究，本人深受启发，本文运用柯西不等式，特别是柯西不等式的变形形式，对文1和文2中给出的一些课本上的习题、高考题、竞赛题进行证明，以供大家探讨.

柯西不等式：若a1，a2，…，an，b1，b2，…，bn是实数，则（a12+a22+…+an2）（b12+b22+…+bn2）≥（a1b1+a2b2+…+anbn）2，当a1，a2，…，an，b1，b2，…，bn不全为零时，等号成立，当且仅当存在一个实数k，使得ai=kbi（i=1，2，…，n）.

柯西不等式的变形形式：若a1，a2，…，an为实数，b1，b2，…，bn为正数，则a1，a2，…，an，b1，b2，…，bn不全为零时，等号成立，当且仅当存在一个实数k，使得ai=kbi（i=1，2，…，n）.

例1 （选修4-5第41页第1题）已知a，b，c∈R+，且a+b+c=1，求证≥9.你能否把这一结论推广，并写出证明.

证明：因为a，b，c∈R+，且a+b+c=1，由柯西不等式的变形公式，得

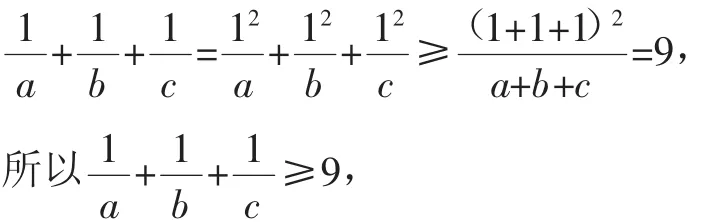
推广：x1，x2，…，xn，∈R+，且x1+x2+…+xn=1，则

证明：因为x1，x2，…，xn，∈R+，且x1+x2+…+xn=1，

由柯西不等式的变形公式，得

例2 （选修4-5第41页第4题）已知a，b，c是互不相等的正数，求证

证明：因为a，b，c是正数，由柯西不等式的变形公式，得

又因为a，b，c是互不相等的正数，

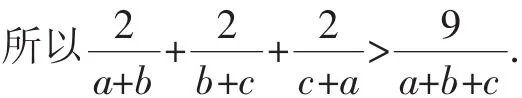
例3 （选修4-5第41页第6题）设x1，x2，…，xn，∈R+，且x1+x2+…+xn=1，求证

证明：因为x1，x2，…，xn，∈R+，且x1+x2+…+xn=1，

又a＞0，b＞0，由柯西不等式的变形公式，得

=1，即a=2，b=4时，等号成立.

所以2a+b的最小值为8.

例5 （2008年陕西卷第22题（3））已知数列{an}的首项，n=1，2，….证明

所以原不等式成立.

例6（2012年全国数学联赛甘肃预赛第11题）设a，b，c为正实数，且a+b+c=1，求证

证明：因为a，b，c为正实数，所以a2+b2+c2≥ab+bc+ca.

又a+b+c=1，由柯西不等式的变形公式，得

拓展：设ai，bi（i=1，2，…，n）同号且不为0，则，当a1，a2，…，an，b1，b2，…，bn不全为零时，等号成立，当且仅当存在一个实数k，使得ai=kbi（i=1，2，…，n）.