对一道三次函数问题引发的多解探究

☉内蒙古自治区海拉尔第二中学 刘 天

☉北京师范大学鄂尔多斯附属学校高中部 岳金燕

三次函数图像的对称中心问题，一直是热点问题之一.同一数学问题，可以从多方位、多角度、多层次入手，就会得到多种解题思路和方法，从而提高对数学知识的理解和掌握，同时也提升数学解题能力，培养优良的数学素养.

例题 已知直线l与曲线f（x）=x3-6x2+13x-9依次交于点A，B，C，且|AB|=|BC|=，则直线l的方程为______.

分析：解决本题的关键是通过定义法或导数法确定三次函数的图像的对称中心坐标，再利用题目条件，通过定义法思维、参数方程、三次方程或数形结合等思维方法来解决过对称中心且满足条件的直线方程问题.而如何快捷地从对称中心入手与直线方程联系起来，这也是解决本题的一大难点，以及思维发散性的体现.结合条件确定点B为三次函数的图像的对称中心，设出B（m，n），结合定义建立关系式，对比系数确定参数m，n的值，即得点B的坐标，进而设出直线l的方程为y-1=k（x-2），代入曲线方程确定其解的问题，进而确定点A的坐标，利用|AB|=|BC|=建立关系式来求解参数k的值，进而得以求解直线l的方程.

设B（m，n），则有（fx）+（f2m-x）=2n恒成立，即x3-6x2+13x-9+（2m-x）3-6（2m-x）2+13（2m-x）-9=2n，展开整理可得（6m-12）x2+（24m-12m2）x+（8m3-24m2+26m-18）=2n.

要使得等式对任意x恒成立，

设直线l的方程为y-1=k（x-2），即y=kx-2k+1，代入（fx）=x3-6x2+13x-9，整理可得x3=6x2+（k-13）x+10-2k.

而x3-8=6x2+（k-13）x+2-2k，则（x-2）（x2+2x+4）=（x-2）（6x+k-1），即（x-2）（x2-4x+5-k）=0，解得x=2或x=2±

那么直线l的方程为y=2x-3.

故填：y=2x-3.

通过对曲线（fx）=x3-6x2+13x-9进行两次求导，并利用f（″x）=0得到x的值，代入曲线得到对应y的值，此坐标（2，1）即为曲线（fx）=x3-6x2+13x-9的对称中心，进而得到对称中心为B（2，1），进而设出直线l的参数方程，代入曲线方程，求得tanθ的值，即为直线l的斜率k，利用直线的点斜式方程求解即可.

解法2：对于曲线（fx）=x3-6x2+13x-9，则有f′（x）=3x2-12x+13，可得f（″x）=6x-12.

令f（″x）=0，得x=2，代入（fx）=x3-6x2+13x-9，得（fx）=1，则曲线（fx）=x3-6x2+13x-9的对称中心为（2，1）.

那么直线l的方程为y-1=2（x-2），即y=2x-3.

故填：y=2x-3.

通过对曲线（fx）=x3-6x2+13x-9进行两次求导，并利用f（″x）=0得到x的值，代入曲线得到对应y的值，因此点（2，1）即为曲线（fx）=x3-6x2+13x-9的对称中心，进而得到对称中心为B（2，1），设出三点对应的横坐标，得到对应的三次方程，进而确定直线l的方程，结合|AB|=|BC|=，建立相应的方程求解参数值即可得到直线l的方程.

解法3：对于曲线（fx）=x3-6x2+13x-9，则有f′（x）=3x2-12x+13，可得f（″x）=6x-12.

令f（″x）=0，得x=2，代入（fx）=x3-6x2+13x-9，得（fx）=1，则曲线（fx）=x3-6x2+13x-9的对称中心为（2，1）.

设A，B，C三点的横坐标依次为2-m，2，2+m（m＞0），则其是方程x3-6x2+ax+b=0的三解，所以a=12-m2，b=2m2-8，即直线l的方程为y=（1+m2）x-2m2-1.

那么直线l的方程为y=2x-3.

故填：y=2x-3.

通过对曲线f（x）=x3-6x2+13x-9进行两次求导，并利用f″（x）=0得到x的值，代入曲线得到对应y的值，因此点（2，1）即为曲线f（x）=x3-6x2+13x-9的对称中心，进而得到对称中心为B（2，1），结合坐标平移变换得到坐标原点位于B时所对应的函数g（x），通过数形确定点A的坐标，进而求解此时的直线方程，再回归坐标平移变换前的点的情况求解直线l的方程即可.

解法4：对于曲线f（x）=x3-6x2+13x-9，则有f′（x）=3x2-12x+13，可得f″（x）=6x-12.

令f″（x）=0，得x=2，代入f（x）=x3-6x2+13x-9，得f（x）=1，则曲线f（x）=x3-6x2+13x-9的对称中心为（2，1）.

设函数g（x）=（fx+2）-1=x3+x，而A（1，2）满足|OA|=，如图1所示，可得直线OA的方程为y=2x，故直线l的方程为y-1=2（x-2），即y=2x-3.

故填：y=2x-3.

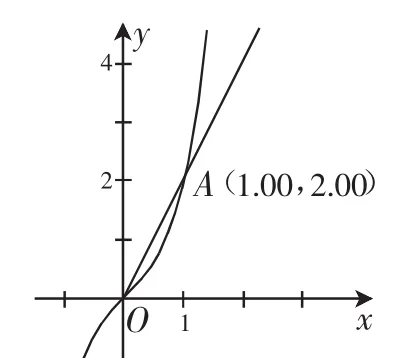
图1

总评：以上解法中，通过定义法与导数法来确定三次函数的图像的对称中心，还可以利用平面向量的平移变换法，以及特殊值法来确定三次函数的图像的对称中心.其实，任何一个三次函数f（x）=ax3+bx2+cx+d（a≠0）的图像都有对称中心，其对称中心为在一些具体问题的过解过程中，特别是选择题或填空题，经常可以直接利用这个结论来确定其对称中心.如果已经攻克这个三次函数的图像的对称中心，那么剩下就是具体如何确定过对称中心且与距离有关的直线方程问题，可以通过以上定义法、参数方程法、三次方程法及数形结合法等来处理.特别是数形结合法处理选择题或填空题中，经常以巧取胜，直观但不具有太强的逻辑性.

当我们解完一道题以后，要不断领悟反思，多角度切入进行深度挖掘，从而达到触类旁通、一题多解的效果.通过典型实例的一题多解，可以使得我们的解题思路更加开阔，数学知识的掌握更加熟练，同时思维拓展，妙法顿生，提高解题速度，培养发散思维能力，有助于激发我们学习的主动性、积极性和趣味性，从而全面提高我们的知识水平和思维能力.H