数控机床高速高加速进给下的跟随误差控制策略
2018-12-12吕盾李润泽刘辉赵万华卢秉恒
吕盾,李润泽,刘辉,赵万华,卢秉恒
(西安交通大学机械制造系统工程国家重点实验室,710054,西安)
高速机床是航空结构件、航空发动机整体叶轮和航天发动机诱导轮等复杂零件加工所必须的关键装备,是支撑航空航天及能源工程等高端装备制造业的基础。当前我国在复杂零件的高速加工中,加工效率和精度难以统一是急需解决的主要问题之一[1]。造成这一问题的主要原因在于,高速机床在加工复杂零件的过程中,各进给轴的跟随误差难以控制。为降低各轴跟随误差,往往只能降低进给速度加速度,牺牲了加工效率。因此,如何保证高速高加速下的高跟随精度,是实现高速机床效率与精度统一的关键问题[2]。
跟随误差是伺服进给系统的实际位置与指令位置的差值。跟随误差的大小取决于伺服进给系统接收的位置指令(或速度指令)和伺服进给系统自身的伺服特性。在高速高加速进给下,各轴位置指令的高频成分增多、频宽增大,对伺服进给系统的伺服特性提出了更高的要求[3]。为了降低高速高加速进给过程中的跟随误差,必须改善伺服进给系统的幅频和相频特性[4]。
改善伺服进给系统的幅频特性主要是提高位置环带宽。伺服进给系统相当于一个低通滤波器,位置环带宽限制使得位置指令中的高频分量被衰减,输出无法及时响应输入,造成跟随误差。伺服进给系统位置环带宽的高低受到机械系统动态特性的限制。对于典型的滚珠丝杠进给系统,丝杠的一阶和二阶扭转模态是限制位置环带宽的主要原因[5],Kamalzadeh采用陷波滤波器补偿丝杠的扭转模态,提高了位置环带宽[6]。此外,文献[7-11]采用滑模及H∞控制等先进控制器,改善了伺服带宽。
改善伺服进给系统相频特性的代表性成果是Tomizuka提出的零相差跟踪控制器(ZPETC)[12],该控制器通过对系统模型的逆设计,实现了输入输出间的相位滞后为0、静态增益为1。此后,该方法与摩擦力补偿、反向间隙及轮廓误差补偿[13]、自适应控制[14-15]、干扰观测器[16-17]及鲁棒控制器[18]、指令整形与模糊逻辑[19]等方法结合,进一步增强了伺服进给系统抗参数变化的能力和抗干扰能力。
综上所述,当前国际上对高速高加速进给下的跟随误差控制策略研究已形成一系列成果,先进的机床制造商在高速高加速进给下跟随误差控制上也达到了一定水平。但是,国内的相关理论研究和工业应用仍然存在非常大的差距,而这一差距也正是国产机床与先进进口机床在性能上差距的主要体现[20]。本文提出一种模态滤波器(MFC)与零相差跟踪控制器综合控制策略,分别改善伺服进给系统的幅频和相频特性,实现高速高加速进给下跟随误差的控制。
1 模态滤波器与零相差跟踪控制器综合控制策略
1.1 模态滤波器设计
首先建立滚珠丝杠进给系统机械部分的等效动力学模型。为表征滚珠丝杠的一阶、二阶扭转模态,将丝杠等效为四惯量弹簧阻尼系统。此外,将电机等效为转子惯量,将联轴器等效为扭转弹簧,将滑块、丝杠螺母副及丝杠轴承等效为弹簧阻尼单元,将工作台等效为刚体。
电机转子的动力学方程为
(1)
式中:J0为电机转子的转动惯量;Kθ0为联轴器的扭转刚度;T0为电机驱动力矩;θ0为电机转子的角位移;θ1为丝杠等效惯量m1的角位移。
滚珠丝杠扭转方向的动力学方程为
(2)
式中:Ji为丝杠各等效惯量的转动惯量,i=1,2,3,4;θi为丝杠各等效惯量的角位移,i=1,2,3,4;Kθi为丝杠各等效惯量间的扭转刚度,i=1,2,3;Kn为丝杠螺母副刚度;Bn为丝杠螺母副阻尼;di为工作台质心相对于螺母轴心、外力方向、工作台顶端以及滑块中心的距离,i=1,2,3,4;p为丝杠导程;Bθi为丝杠各等效惯量间的等效阻尼,i=1,2,3。
滚珠丝杠轴向的动力学方程为
(3)
式中:mi为丝杠各等效惯量的质量,i=1,2,3,4;Ki为丝杠各等效惯量间的轴向刚度,i=1,2,3;K0、K4为丝杠轴承支承刚度;xi为丝杠各等效惯量的轴向位移,i=1,2,3,4;B0、B4为丝杠轴承阻尼。
工作台的动力学方程为
(4)
式中:mt为工作台质量;Jt为工作台转动惯量;Bt为导轨滑块副阻尼;Kt为导轨滑块副刚度;B5为滑块沿进给方向运动时的摩擦阻尼;Ft为外力。
综合式(1)~(4),滚珠丝杠进给系统的动力学方程可表达为
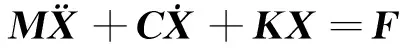
(5)
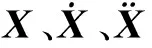
由式(5)可得滚珠丝杠进给系统电机处力入编码器速度出的传递函数为
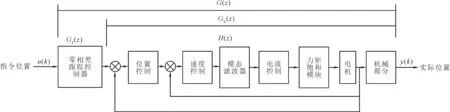
图1 模态滤波器与零相差跟踪控制器综合控制策略仿真模型框图
(6)
根据式(6),求解滚珠丝杠进给系统电机力入编码器速度出的频响曲线,可以获得丝杠的一阶和二阶扭转振动振型及固有频率。
由式(6)求解一阶和二阶扭转振动模态的零极点。设计模态滤波控制器H(z),使其零极点与一阶和二阶扭转模态零极点相抵消,削弱这两阶扭转模态对位置环带宽的限制作用。
1.2 零相差跟踪控制器设计
对加入模态滤波器后伺服进给系统的传递函数进行辨识,以设计零相差跟踪控制器。辨识模型采用离散传递函数形式
(7)
式中:u(k)和y(k)分别为进给系统的输入和输出;d为进给系统的延时周期数。
辨识得到的伺服进给系统离散传递函数为
(8)
式中:d表示系统延时,A(z-1)和B(z-1)为互质的离散多项式。
理论上,零相差跟踪控制器Cr(z)应取伺服进给系统传递函数Gc(z)的逆。然而,当Gc(z)为非最小相位系统时,B(z-1)会存在不稳定的零点,导致控制器不稳定。因此,将B(z-1)分解为
B(z-1)=Ba(z-1)Bu(z-1)
(9)
式中:Ba(z-1)为单位圆内的系统零点组成的多项式;Bu(z-1)为单位圆外和单位圆上的系统零点组成的多项式。
零相差跟踪控制器的传递函数为
(10)
加入零相差跟踪控制器后,系统的传递函数变化为
(11)
系统输入变为u(k+d+s),表示超前于需要输入值u(k)d+s步,s为不稳定零点个数。
1.3 综合控制策略仿真模型
将设计得到的模态滤波器与零相差跟踪控制器集成到PID控制框架中,建立综合控制策略的仿真模型,模型为连续模型,指令周期为2 ms,如图1所示,其中模态滤波器设置在速度环内,零相差跟踪控制器设置在位置环之前。
2 实验验证
2.1 实验装置
实验装置为铣床X轴进给系统,如图2所示。该进给系统为滚珠丝杠传动,电机为伺服交流电机,型号为SGMGH-30ACA,驱动器为SGDM30ADA。进给系统采用半闭环控制,增量式码盘线数为2 500,速度环采样时间为250 μs。数控系统为PA开放式数控系统。通过查阅机床相关手册以及数控系统和驱动器内的参数设定,建模所需参数如表1所示。

图2 实验装置照片

表1 机床相关参数
2.2 滚珠丝杠进给系统等效动力学模型实验验证
滚珠丝杠进给系统等效动力学模型的准确性是模态滤波器设计的基础。为了验证等效动力学模型,给电机施加快速正弦扫频激励力信号,得到电机力入编码器速度出幅频响应,如图3所示。图3的实验结果表明,滚珠丝杠进给系统存在6阶固有频率,分别为20.2、49.8、70.8、121.6、378.9和941.4 Hz,其中378.9和941.4 Hz为一阶和二阶扭转振动的固有频率。理论计算得到的一阶和二阶扭转振动的固有频率分别为378和957.3 Hz。一阶和二阶扭转振动固有频率的实验测试结果和理论计算结果基本一致,可以证明所建立等效动力学模型及模态滤波器设计的准确性。
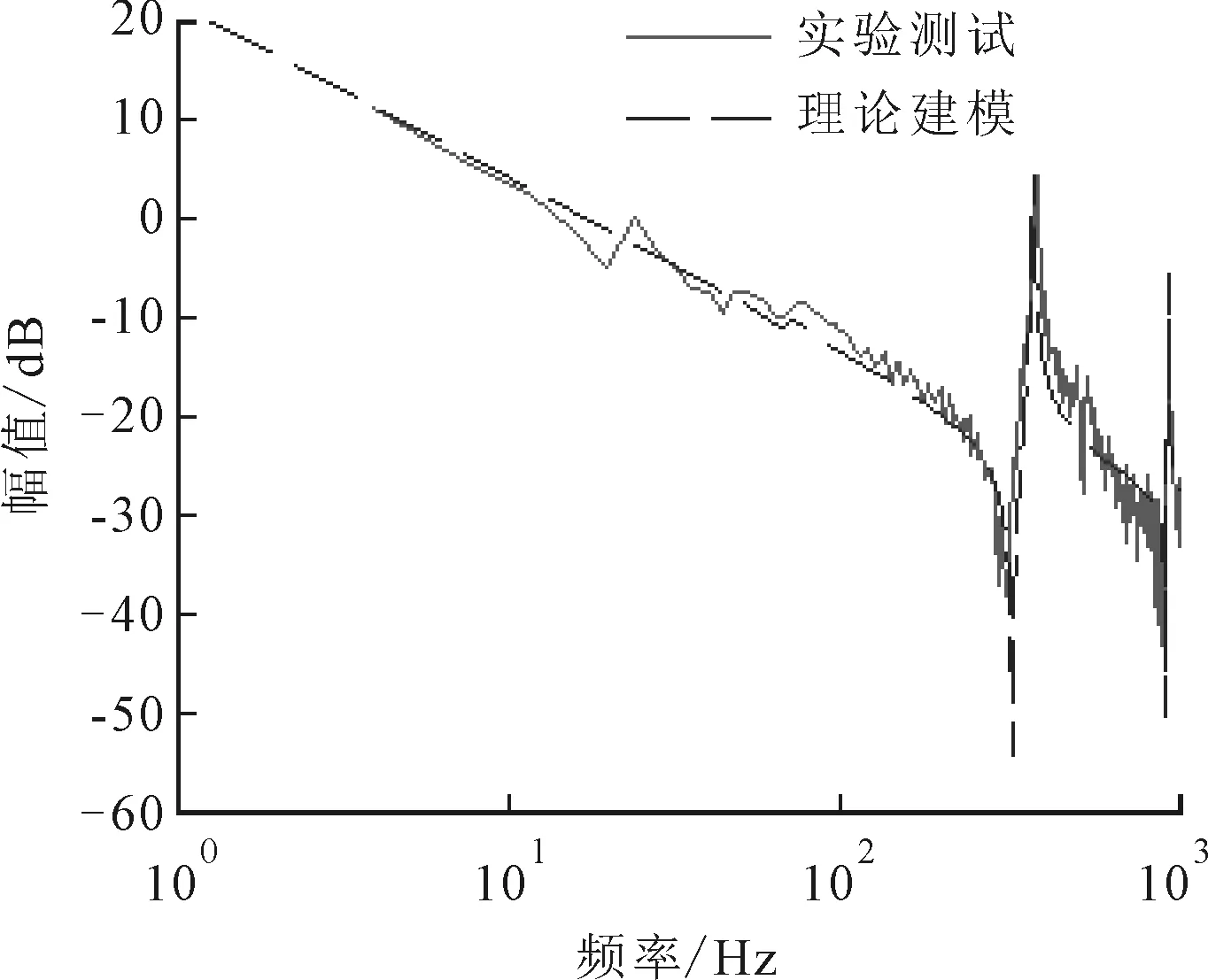
图3 滚珠丝杠进给系统电机力入编码器速度出幅频响应
2.3 伺服进给系统传递函数辨识及零相差跟踪控制器求解
辨识信号采用10 m/min匀速直线运动和幅值为40 μm的M序列的叠加信号。将辨识信号作为插补指令输入数控系统,同时采集编码器反馈的输出位移信号,采样周期为2 ms。根据1.2节所述方法,求解零相差跟踪控制器传递函数。
2.4 伺服进给系统实际位置的理论仿真与实验测试对比
令X轴做直线往返进给运动,指令位置u(k)的速度变化曲线如图4所示。最大速度为10 m/min,加速度为2 m/s2,加减速策略为S型,行程为200 mm。
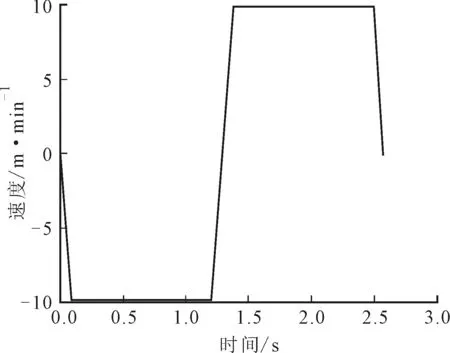
图4 进给运动的速度曲线
图5a为实际位置y(k)的理论仿真与实验测试结果,从图5b中可以看出,理论仿真与实验测试结果非常吻合,二者之间的差异小于0.1 μm,证明了第1节所建立的综合控制策略仿真模型的正确性。
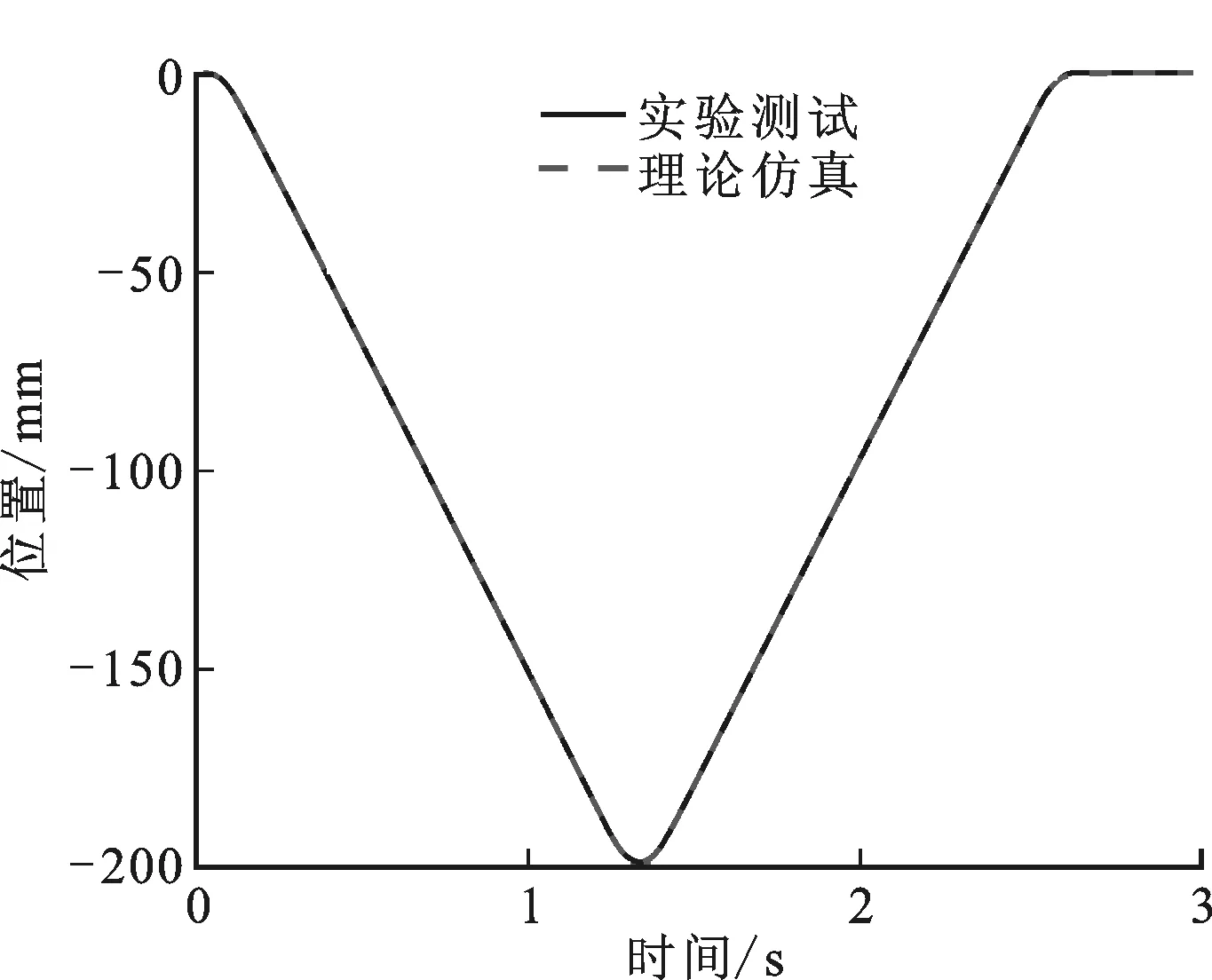
(a)实验测试与理论仿真结果对比

(b)实验测试与理论仿真结果之差
3 控制效果及分析
在实验验证了所建立综合控制策略仿真模型正确性的基础上,利用该仿真模型进一步分析综合控制策略对高速/高加速下跟随误差的控制效果。在仿真模型中输入如图4所示变化趋势的速度指令,其速度分别为10、20、30和50 m/min,加速度分别为2、5和10 m/s2,行程为1 m。
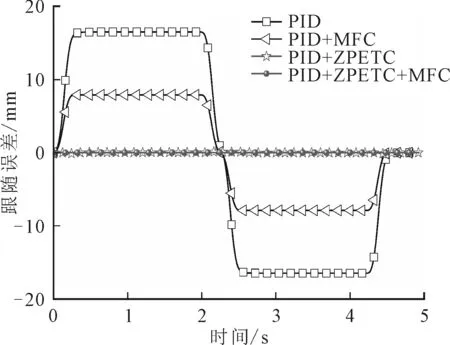
图6 4种控制策略下跟随误差随时间的变化
图6示出了速度为30 m/min、加速度为10 m/s2时,4种控制策略下,跟随误差在整个行程上(随时间)的变化。从图6中可知,在PID、PID+MFC、PID+ZPETC和PID+ZPETC+MFC这4种控制策略下,跟随误差最大值分别为16.486、7.907、0.150和0.016 mm。
由图6可见,PID控制策略下的跟随误差非常大,这主要是由于伺服系统的相位滞后而引起的。采用PID+ZPETC控制策略,相对于PID及PID+MFC控制策略,显著缩小了相位滞后,如图7所示,因此跟随误差大幅降低。

图7 伺服进给系统在不同控制策略下的相频曲线
相位滞后的改善,显著减小了跟随误差。此时,引起跟随误差的主要原因变为伺服进给系统位置环带宽的限制。由于加减速过程中指令的频宽较匀速过程大,因此,PID+ZPETC控制策略下,跟随误差在加减速过程中比较突出。采用PID+ZPETC+MFC控制策略,在保证较小相位滞后的前提下,进一步提高了伺服系统的位置环带宽,如图8所示,因此,跟随误差进一步减小。

图8 伺服进给系统在不同控制策略下的幅频曲线
图9所示为采用PID+ZPETC+MFC控制策略,不同进给速度加速度下的最大跟随误差,其中加速度为0表示匀速过程中的最大跟随误差。
从图9中可以看出:在PID+ZPETC+MFC控制策略下加减速过程中的跟随误差大于匀速过程;在某一加速度下,跟随误差随着速度的增大而增大;在某一速度下,跟随误差随着加速度的增大而增大;当进给速度为50 m/min、加速度为10 m/s2时,跟随误差大幅增大到188.3 μm。造成跟随误差大幅增大的原因是,高速/高加速需要的电机扭矩超出了电机限制,如图10所示。
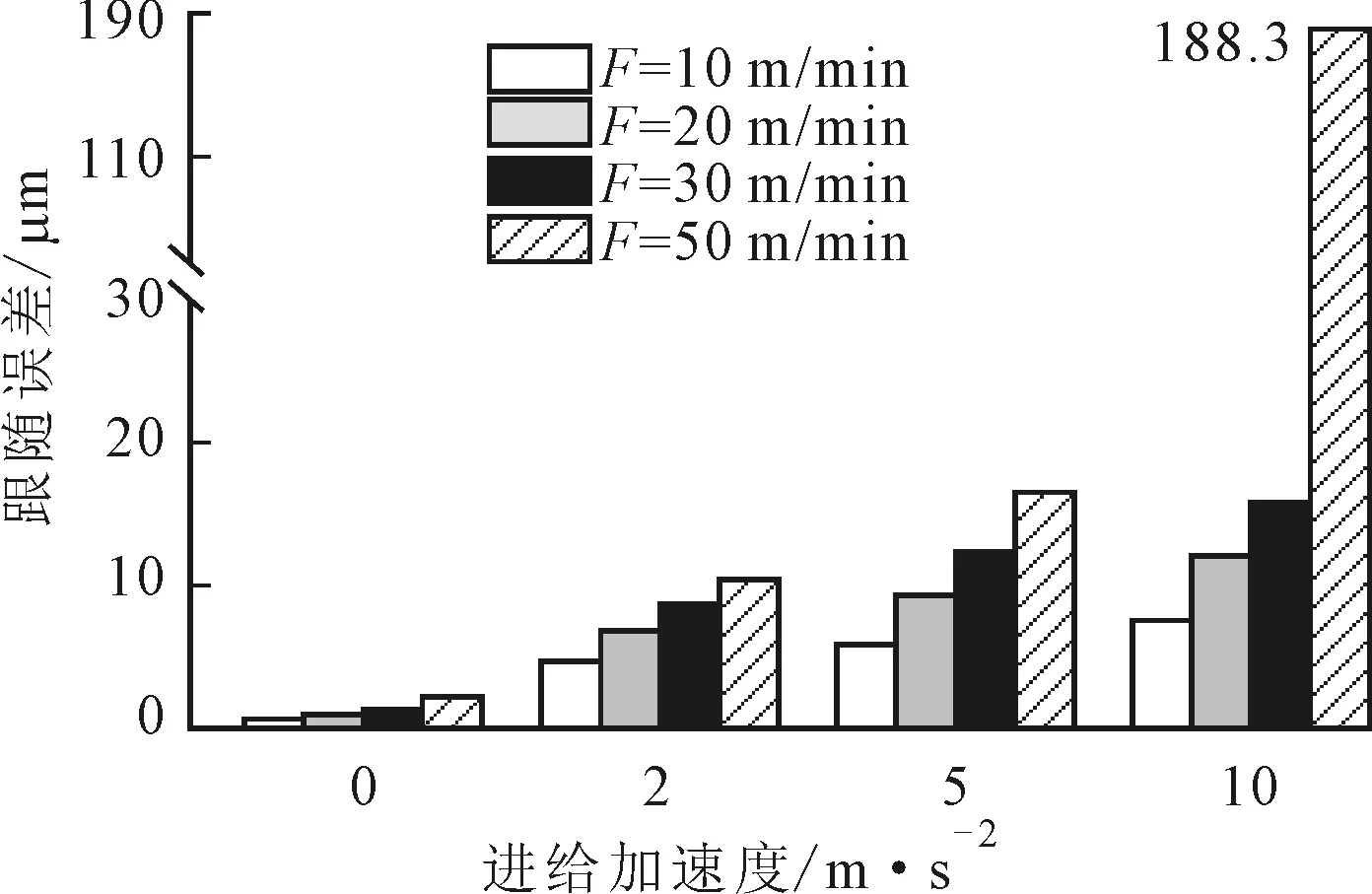
图9 PID+ZPETC+MFC控制策略在不同速度和加减速下的跟随误差

图10 高速高加速需要的电机扭矩与电机实际输出扭矩对比
4 结 论
(1)PID+ZPETC+MFC控制策略改善了伺服进给系统的相位滞后、提高了伺服进给系统的位置环带宽,当进给速度为30 m/min、加速度为10 m/s2时,将跟随误差由PID控制策略下的16.486 mm大幅降低到15.5 μm。
(2)PID+ZPETC+MFC控制策略下,匀速过程中的跟随误差很小,加减速过程中的跟随误差相对突出,且跟随误差随速度及加速度的增大略微增大。
(3)随着速度和加速度的增大,所需要的电机扭矩也不断增大,当需要的电机扭矩超过电机扭矩限制时,PID+ZPETC+MFC控制策略不能再对跟随误差实施有效控制。
