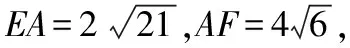例谈立几中无棱二面角的纯几何解法
2018-12-07广东李光喜
广东 李光喜
在立体几何中,有一类无棱二面角的问题,只在图形中给出了二面角的两个半平面的一个公共点,没有给出二面角的棱,学生在解答时往往因为找不到二面角的棱而感到无从下手.下面笔者举例说明这类二面角的五种纯几何求法,对培养学生的空间想象和逻辑推理能力不无帮助.
一、延长线段找棱法
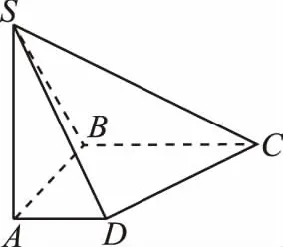
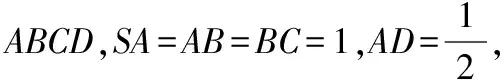
分析:要求平面SCD与平面SBA所成二面角的正切值,必先确定所求二面角的平面角,而所求二面角的棱在图中未给出,故关键是先确定二面角的棱.为此,延长BA,CD相交于点E,连接SE,则SE是所求二面角的棱.下面先证明∠BSC是所求二面角的平面角.
【解析】∵AD∥BC,BC=2AD,∴EA=AB=SA,
∴SE⊥SB.
∵SA⊥平面ABCD,
∴平面SEB⊥平面EBC,EB是交线,又BC⊥EB,
∴BC⊥平面SEB,∴BC⊥SE,又BC∩SB=B,
∴SE⊥平面SBC,则SE⊥SC,
故∠BSC是所求二面角的平面角.


评注:当已知二面角的两个面在图中只有一个交点,但易在二面角的两个面内找到两条相交直线时,常用办法是延长两条线段得到二面角的两个面的另一个交点,从而确定二面角的棱,再用线面垂直找出或作出平面角,从而求出二面角,这种方法我们不妨称之为延长线段找棱法.
二、线面平行找棱法
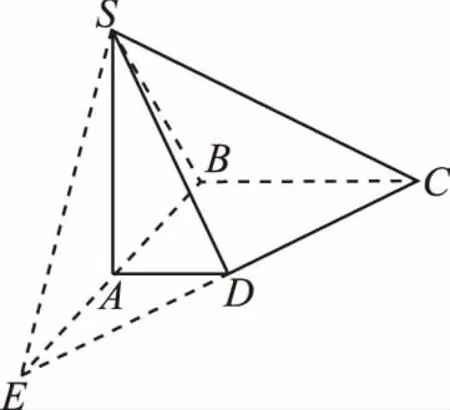
【例2】如图,ABCD为矩形,M是AB的中点,PA⊥平面ABCD,PA=AD=1,AB=2.
(1)求平面PAD与平面PMC所成二面角的正切值;
(2)求平面PAD与平面PBC所成二面角的正切值.
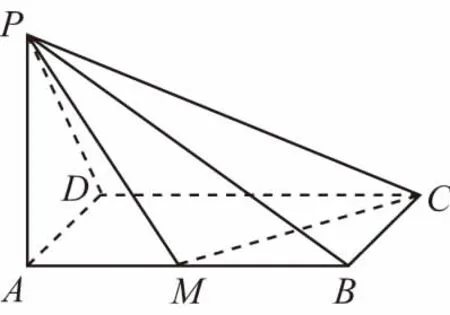

(2)平面PAD与平面PBC所成二面角的棱在图中未给出,不能利用上述延长线段找棱法求解,但可利用线面平行的性质定理找出平面PAD与平面PBC所成二面角的棱来解.
∴BC∥平面PAD.
又平面PAD与平面PBC相交于点P,
∴平面PAD与平面PBC相交于过点P的一条直线,
记为l,则直线l为平面PAD与平面PBC的棱,
根据线面平行的性质定理可知BC∥直线l,
∵PA⊥平面ABCD,∴PA⊥BC,
又AB⊥BC,AB∩PA=A,
本文提出一种新型的隧道位移预测方法,在小波变换下,将模糊控制和Elman网络结合,实现了对隧道位移的预测,与其他方法相比,主要有以下优点:
∴BC⊥平面PAB,故直线l⊥平面PAB,
∴PA⊥直线l,PB⊥直线l,则∠BPA是所求二面角的平面角,

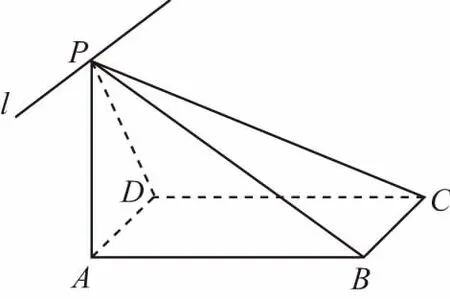
评注:当已知二面角的两个面在图中只有一个交点,且在一个面内有一条直线和另一个平面内的一条直线互相平行时,则可用线面平行的性质定理找出所求二面角的棱,从而转化为有棱的二面角去求,这种方法我们不妨称之为线面平行找棱法.
三、构造长方体(正方体)找棱法
【例3】如图,ABCD为矩形,PA⊥平面ABCD,PA=AD=1,AB=2,求平面PAD与平面PBC所成二面角的正切值.
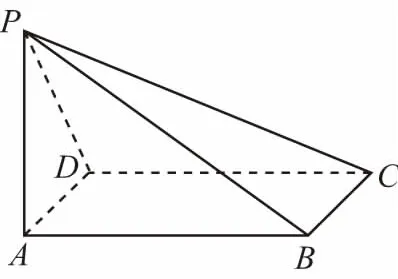
分析:平面PAD与平面PBC所成二面角的棱在图中未给出,可将图形补成以AP,AB,AD为棱的长方体ABCD-PMNE.
【解析】补形后的图形如图,易知PE就是平面PAD与平面PBC所成二面角的棱.则∠BPA是所求二面角的平面角,
在Rt△PBA中,PA=1,AB=2,


评注:当已知二面角的两个面在图中只有一个交点,且已知图形可以看成长方体(正方体)的一部分时,则可构造长方体(正方体)找出所求二面角的棱,从而转化为有棱的二面角去求,这种方法我们不妨称之为构造长方体(正方体)找棱法.
四、平移平面法
【例4】如图,在正四棱锥P-ABCD中,AB=2,PA=3,求平面PAD与平面PBC所成二面角的余弦值.
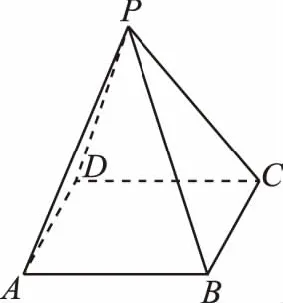
分析:平面PAD与平面PBC所成二面角的棱在图中未给出,利用例1中的延长线段找棱法,不能作出二面角的棱,这时可通过平行移动平面PBC的办法求二面角.为此,在平面PCD内,过D作线段FD与PC平行且相等,连接PF,AF,易证平面FAD∥平面PBC,故平面FAD与平面PAD所成二面角的大小等于平面PAD与平面PBC所成二面角的大小.

【解析】取AD的中点E,连接PE,EF,易证FA=FD,
又PA=PD,
∴PE⊥AD,FE⊥AD,
故∠PEF是平面FAD与平面PAD所成二面角的平面角.
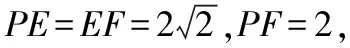
评注:当已知二面角的两个平面在图中只有一个交点,且在一个平面内有一条直线和另一个平面内的一条直线互相平行时,常用办法是平移其中一个平面和另一个平面相交,从而转化为有棱的二面角去求,这种方法我们不妨称之为平移平面法.
五、射影法
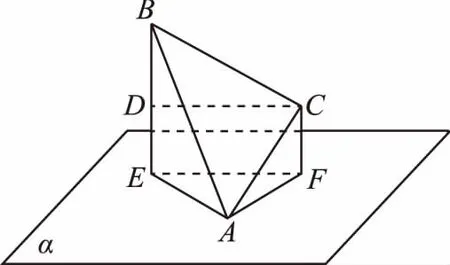
【例5】如图,正三角形ABC的边长为10,A∈平面α,B,C到平面α的距离分别为4和2,B,C在平面α的同侧,求平面ABC与平面α所成二面角的余弦值.


【解析】过B,C分别作BE⊥平面α于E,
CF⊥平面α于F,则BE∥CF,
且BE=4,CF=2,∵BA=AC=10,