对一道高三模拟题的多视角探析及思考

江苏 陈业代

高三复习阶段，许多学生都感觉解析几何题难度大、运算繁，若题目稍有“拐弯抹角”，就无计可施，甚至不能理解题意，不会运用转化思想，不能化陌生为熟悉、化复杂为简单，方向感不明确，当然就找不到解决问题的最佳途径．最近笔者所教班级做了2017年南通、泰州市高三一模涉及圆的一道模拟题，全班45人参考，3人会做，仅有1人做对．从学生中了解到的情况是不知从何处下手或涉及变量太多不敢算下去．

1．问题呈现

在平面直角坐标系xOy中，已知B，C为圆x2+y2=4上两点，点A(1，1)，且AB⊥AC，则线段BC的长的取值范围是 .

2．问题探析

视角1 “基本不等式”法——已知两点B,C在圆上且通过条件“AB⊥AC”联系起来，显然通过设点B(a,b),C(c,d)建立三个等式，运用等式的恒等变形和基本不等式相关知识即可求解．

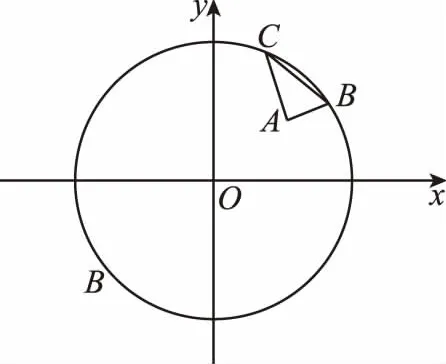
解析：设B(a,b),C(c,d)，

即ac+bd=a+c+b+d-2，

∵B,C在圆x2+y2=4上，

整理得(a+c)2+(b+d)2=8+2(ac+bd)，

令ac=m,bd=n，

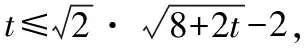
评注：这是一道填空小题，这么完成的推理过程对运算能力要求很高，耗时是必然的，经询问学生用了近15分钟，显然这个方法“性价比”不高．

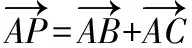
则(x-1,y-1)=(x1+x2-2,y1+y2-2)，

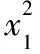
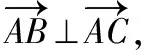
∴(x1-1,y1-1)·(x2-1,y2-1)=0，x1x2+y1y2-x1-x2-y1-y2=-2，

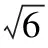
解析：过点O作OD⊥AB于D，作OE⊥AC于E，设OD=d1,OE=d2，由平面几何知识得，

∵AB⊥AC，

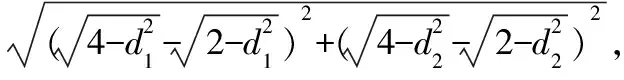
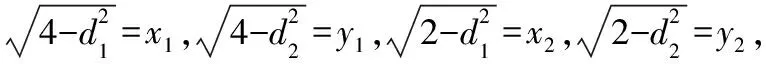
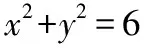
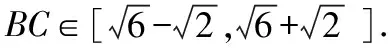
评注：这个解法运算简单，但思维量较大，要具备较高的逻辑推理能力，另外，学生不易想到构造距离．

视角4 “纯几何”法——运用矩形性质直接探索出点P的轨迹．

评注：显然此解法比较简单，比较适合解填空题，但是这个矩形性质不常用，没参加过竞赛辅导的学生也是不易想到的．

3．几点思考

(1)本题是从四个不同视角探求并解决问题，方法各有千秋，为了补偿纠正以达到高三复习效果，可作如下变式：

在直角坐标系中，圆C1:x2+y2=4，圆C2:x2+y2=16，点M(1，0)，动点P,Q分别在圆C1和圆C2上，满足MP⊥MQ，则线段PQ长的取值范围是 .

(2)本题是解析几何综合题中的一个代表，视角1易想难算，视角2、视角3、视角4难想易算，这是解析几何的最大特点，即要么运算量大，要么思维量大，作为考试题具有一定选拔功能．从四种解法可总结出共性问题，即涉及长度问题转化为上，这就是我们常说的通性通法．这就需要我们把它贯穿于平时的教学当中去，以实现教学效果最大化．

(3)本题作为填空题，显然无法展现学生的思维过程，能完成本题解答的学生很少，作为考试题，区分度不大，大都不会做，失去了考查的目的，如果改成解答题，那么学生还能写点东西，能体现出学生多样的思维方式和层次性，这样效果应该会更好些．

(4)最直接的选择未必是选择最好的，在上面四种解法中，为什么学生都会从最烦琐的方法1开始探求呢？因为学生喜欢凭感官直觉，其实稍加分析，视角2也是容易接受的，其他几个视角解析途径都“很棒”，却是学生最不易想到的，为了选拔考试，把题做对才是“王道”，因此，在高三解题教学中，要教会学生对待解决问题的方案要善于选择，选择适合自己的方法，适合的才是最好的．当然平时对学生也要加强思维层次训练，好方法不是教师教出来的，而是组织学生研讨由学生总结感悟出来的．

4．一点感悟