为何偏偏又是它——“y2=4x”

广东 杨伟达

每年高考题无不例外地引起教育同行高度的关注和热议. 同样，今年高考数学试题也如此. 下面是笔者对2018年全国各地高考数学考卷中有关抛物线“y2=4x”的比较和联系，旨在寻找题型的规律，总结解题方法.

一、题目再现

( )

A.5 B.6

C.7 D.8

2.(2018·北京卷文·10)已知直线l过点(1,0)且垂直于x轴，若l被抛物线y2=4ax截得的线段长为4，则抛物线的焦点坐标为________.

3.(2018·全国卷Ⅲ理·16)已知点M(-1,1)和抛物线C：y2=4x，过C的焦点且斜率为k的直线与C交于A，B两点.若∠AMB=90°，则k=________.

4.(2018·全国卷Ⅱ·理19，文20)设抛物线C：y2=4x的焦点为F，过F且斜率为k(k>0)的直线l与C交于A，B两点，|AB|=8.

(Ⅰ)求l的方程；(Ⅱ)求过点A，B且与C的准线相切的圆的方程.

5.(2018·北京卷理·19)已知抛物线C：y2=2px经过点P(1,2).过点Q(0,1)的直线l与抛物线C有两个不同的交点A，B，且直线PA交y轴于M，直线PB交y轴于N.

(Ⅰ)求直线l的斜率的取值范围；

6.(2018·浙江卷·21)如图，已知点P是y轴左侧(不含y轴)一点，抛物线C：y2=4x上存在不同的两点A，B满足PA，PB的中点均在C上.

(Ⅰ)设AB中点为M，证明：PM垂直于y轴；

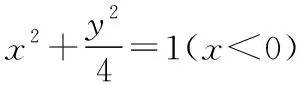
纵观上面各地考卷试题，离不开一条熟悉的抛物线：y2=4x，离不开直线与抛物线相结合这一永恒主题.

二、解答过程与思路剖析

对一道高考试题的求解，关键是审题！题目已知条件、结论、已知量、未知量、常见的相关类型题及解题思路等都需要在做题前一一弄明白.

1.方程组+向量坐标运算

分析题设没有涉及长度和夹角，所以可把向量转化为坐标求解，同时涉及直线与抛物线的位置关系，通常列方程组解决问题.

解：由抛物线C：y2=4x可得F(1,0)，

解得x1=1，x2=4，分别代入y2=4x，

因为y>0，所以y1=2，y2=4，

2.点代法

分析本题涉及直线与抛物线的弦长问题，因该直线垂直于x轴，两个交点为特殊点，用代入法可求得.

3.构造圆+点差法

分析本题从∠AMB=90°出发，构造以AB为直径的圆与准线相切，“设而不求”即可求k；也可从列方程组出发，转化为一元二次方程，用坐标表示∠AMB=90°，求得k.

解：如图，过点M(-1,1)作一条垂直于x轴的直线l,则直线l为抛物线C：y2=4x的准线，依题 ∠AMB=90°可构造一个以AB为直径的圆N且与准线相切，圆心N为AB的中点，所以yM=yN=1，

设抛物线上点A(x1,y1)，B(x2,y2)，

因为N是AB的中点，所以y2+y1=2，

所以k=2.

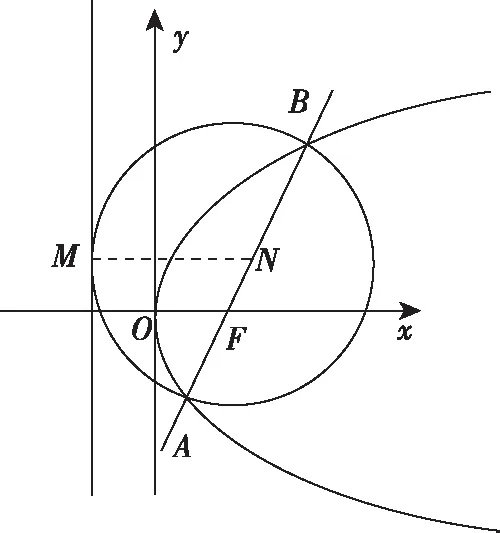
注另一解法是从方程组出发，转化为一元二次方程，利用根与系数的关系，用坐标表示∠AMB=90°即可求得直线的斜率k.

4.方程组+抛物线定义

分析此题涉及直线与抛物线的弦长问题，通过列方程组转化为一元二次方程，利用抛物线的定义，“设而不求”即可. 第二问涉及过两动点、且与准线相切的圆方程问题，利用图形的几何性质，“设而又求”求得圆心和半径，问题解决.

解：(Ⅰ)由抛物线C：y2=4x可得F(1,0) ，设A(x1,y1),B(x2,y2),

所以直线l的方程y=k(x-1)，

化简为k2x2-(2k2+4)x+k2=0，

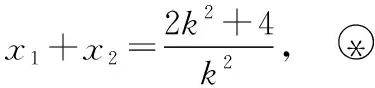
由抛物线的定义可知|AB|=|AF|+|BF|=x1+x2+2,

由|AB|=8得x1+x2=6，

所以直线AB的方程为y=x-1. ①

(Ⅱ)如图，不妨设圆心坐标为N(a,b),半径为r=a+1，

由x1+x2=6得x中点=3，代入①，求得y中点=2,

所以中点M(3,2)，直线AB的中垂线为x+y-5=0.

圆心N在直线AB的中垂线上，则有a+b-5=0，

解得a=3,b=2,r=4，或者a=11,b=-6,r=12，

所以圆的方程为(x-3)2+(y-2)2=16或(x-11)2+(y+6)2=144.

5.点代法+方程组

分析本题涉及直线与抛物线的位置关系，联立方程组转化为一元二次方程即可.第二问涉及向量，需要用坐标形式表示. “设而不求”、代入、消元即可求证.

解：(Ⅰ)抛物线y2=2px过点P(1，2)，

所以4=2p，解得p=2，所以抛物线方程为y2=4x．

由题意可知，设过(0,1)的直线l的斜率为k，则直线l的方程为y=kx+1(k≠0)，

依题意Δ=(2k-4)2-4×k2×1>0，解得k<1(k≠0)，

所以直线l斜率的取值范围是(-∞，-3)∪(-3，0)∪(0，1).

(Ⅱ)证明：不妨设A(x1，y1)，B(x2，y2)，

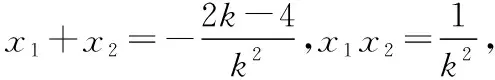
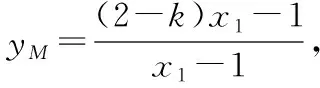
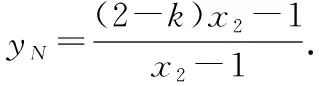
6．点代法+列方程组

分析本题主要考查椭圆、抛物线的几何性质，直线与抛物线的位置关系. 第一问，通过“设而不求”“消元转化”即可求证；第二问，利用第一问的结果，把三角形面积用坐标表示，代入并转化为一元二次函数求最值,即可将问题解决.

因为PA，PB的中点在抛物线上，

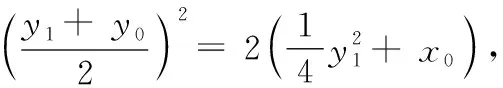
所以y1+y2=2y0．

因此，PM垂直于y轴．

点评纵观前面几道答案，全国Ⅰ卷、Ⅱ卷、Ⅲ卷的解析几何试题给人很传统的感觉，都是平时见过的常规题，运算量不大，其解法在教材中都能找到，侧重考查主干知识和核心思想；而地方卷(北京卷、浙江卷等)尽管与全国卷一样注重数学本质、核心思想、通性通法，但是涉及的动点较多，目标设置有新意，需要考生在运算、消元方面能力更强，需要考生“忙而不乱”“乱而有序”，否则雾里看花、无从下手！

三、追根溯源

源于课本(高中数学人教A版选修2-1课本第69页例4)斜率为1的直线l经过抛物线y2=4x的焦点F，且与抛物线相交于A，B两点，求线段AB的长.

有关抛物线“y2=4x”模型，经笔者查找，课本第69页例4、第71页例6、第72页练习第3题及第4题、第73页习题第5题、第80页第11题都涉及它.在抛物线的教学课堂中，它出现的频率很高，主要考查了直线与抛物线的位置关系、抛物线定义及性质，主要涉及参数、最值、弦长、方程等相关问题.在解题方法上强调高中数学的通性通法，即联立方程组转化为一元二次方程，用判别式和韦达定理化简求解.

源于高考1.(2017·全国卷Ⅰ理·10)已知F为抛物线C：y2=4x的焦点，过F作两条互相垂直的直线l1，l2，直线l1与C交于A，B两点，直线l2与C交于D,E两点，则|AB|+|DE|的最小值为

( )

A.16 B.14

C.12 D.10

考点分析考查了直线与抛物线相交，求弦长和最小值问题. 对抛物线的弦长问题，要抓住抛物线定义，利用直线与抛物线联立方程组，转化为一元二次方程，用判别式、韦达定理求解.这些都是高中数学的通性通法，需要重点掌握；对最值问题，通常想到用函数或者基本不等式来求解.

点评当求得|AB|+|DE|最小值为16时，发现两直线的斜率分别为k=±1，此时|AB|=8，|CD|=8，这就是课本例题4的解法和答案，答案是巧合还是故意设置？这或许是课本例题的延续吧.在强调命题改革的今天，通过改编、创新等手段赋予课本的例题、习题新的生命，这依然是高考命题专家的一种喜好.

四、解后反思

1.与新课标吻合，突显核心素养

数学素养是考生应具备的适应终身发展和社会发展需要的数学领域必备品格和关键能力.必备品格是指具有必要的数学知识，具有数学应用意识、数据意识、和计算意识.关键能力包括空间想象能力、逻辑推理能力、计算能力、数据处理能力，数学抽象和概括能力、数学表达和交流能力.

《普通高中数学课程标准(实验)》明确提出要培养考生“提出问题、分析问题、解决问题”的能力.传统意义上的难题主要集中在解析几何和函数这两大知识块.而今年高考中，解析几何试题的难度略有下降，试题的命制依纲按本，注重数学本质，突出通性通法，符合新课程理念，很好地将知识、思想方法、能力、数学文化、应用意识、创新意识高度融合，题型常见，创新背景不偏不怪，易读懂，运算量不大，解决问题的方法都是高中数学的核心思想.重点考查主干知识，突出思维能力和运用能力.

2.挖掘教材资源，寻找子母题

当前教育的一个现象：许多学生参加完中考或高考后发现课本跟三年前入学派发时的课本一样新！是考生的选择性错误还是教师的引导性错误？什么讲学稿、导学案、校本教材占据考生的大部分时间，从而使得考生无暇顾及课本，造成两者不可兼得的事实.而高考试题常考常新，不可能一模一样，为了避免考生题海战，必须关注、寻找子母题，在子母题中合理的改变条件和求解目标(变条件、变结论、变参数、变方法)，有利于提升考生对核心问题的把握能力，有利于提升考生的思维品质，这需要教师精选好题，深入剖析，合理变式.

子母题所具备的条件：

(1)以联想拓展学生思维

以子母题为原型，引导考生发现问题，对知识点、思想方法的联想，从静态到动态，不断发散考生的思维，不断诱发考生从题设的已知去拓展，去丰富，去完善已有的知识.

(2)以问题引领有效课堂

它具有深刻的历史背景和现实意义(主要指教材教参及高考背景)，具备解决类似问题的通性通法，同时也具有自身的一些特性.教师层层设置问题，为学生提供由易到难，由浅入深的知识链，让考生经历综合题的生成过程.

子母题发挥作用：

它具有代表性、典型性、科学性.在课堂教学中，从子母题出发，引导学生归纳总结解题方法并能熟练掌握，就会大大激发学生的成就感和获得感，由于得到深刻的思考，不少考生在考场中容易找到解题的方案，攻克平时没有头绪的难题，无形中消除了惧怕心理，从而提高考生解决问题的能力.

抛物线“y2=4x”具备子母题的条件：

(1)它不是二元二次齐次方程，二次项的系数为1，比椭圆、双曲线方程来得更简单.而且它的焦点坐标和准线都是0或1的整数，便于运算；(2)用好抛物线定义，可以替换线段的长度.在降低难度、减少运算的情况下，抛物线y2=4x是个最好的选择；(3)它与直线相交，联立方程组转化为一元二次方程时，各项系数来得简单、容易些，同时它还与梯形、三角形、圆等都有很好的结合点.