基于Bonferroni均值算子的跨境电商发展水平直觉模糊评价方法

周金明

(安徽工程大学 数理学院，安徽 芜湖 241000)

跨境贸易电子商务作为一种具有前瞻性的新型跨境贸易模式，引领着全球电子商务的发展潮流.中国跨境电子商务行业仍处于初级发展阶段，投资、融资事件如雨后春笋，整体行业资产快速增长.截止到2015年8月初，全国共有9个跨境电商进口试点城市为宁波、郑州、上海、重庆、杭州、广州、深圳、福州、平潭；全国跨境贸易电子商务服务试点城市包括郑州、杭州、重庆、上海、宁波、广州、深圳、天津共8个城市.2015年，出口跨境电商纷纷转型进口，大量传统外贸开始触及跨境电商；中国跨境电子商务市场规模将达5.3万亿元，同比增长32%;中国跨境电子商务行业交易额占进出口贸易总额19.4%.

针对跨境电商行业发展水平进行评价，可以把握各区域的发展均衡状态，反映电商行业发展趋势和机遇，反映跨境电商的特色和潜在优势等.文献[1]应用“技术—组织—环境”三维框架的思想和要素模型分析方法，在运用扩展关系数据库描述方式的基础上，对跨境电子商务的跨境主体、跨境环境、配套服务三维模型进行了扩展,对我国主要城市跨境电子商务发展水平进行了定量评价和层级划分.杨坚争[2]等通过因子分析法研究得出5个对跨境电子商务发展有重要影响的指标，并应用指标体系对我国各地的跨境电子商务发展状况进行了研究分析.

纵观跨境电子商务发展水平评价的研究，考虑跨境电子商务评价指标的模糊性和不确定性的文献尚不多见.在评价活动中，由于指标之间还存在一定的相互关系，同时要兼顾评价过程科学性原则、可操作性原则与公平原则[3].鉴于此，提出基于加权直觉模糊Bonferroni调和均值算子(WIFBHM)的决策方法，并对某省份跨境电商部分区域发展水平进行测度与评价.

1 Bonferroni算子相关概念

1.1 Bonferroni均值的定义与性质

Bonferroni均值(Bonferroni Mean,简记为BM)算子[3]可以将多个输入变量集结为一个输出变量，是一种介于最大和最小之间的集成算子，它主要的优点是在集成过程中可以反映每一个输入变量与其他输入变量之间的相互关系.

定义1[4]设p,q≥0,ai(i=1,2,…,n)是非负实数集.若

(1)

称其为Bonferroni均值，易知该均值有如下性质：

(1)BMp,q(0,0,…,0)=0.

(2)(幂等性)BMp,q(a,a,…,a)=a.

(3)(单调性)BMp,q(a1,a2,…,an)≥BMp,q(b1,b2,…,bn),即BMp,q是单调的如果ai≥bi,(i=1,2,…,n).

(2)

称其为加权Bonferroni均值(Weighted Bonferroni Mean，WBM).

(3)

称其为加权Bonferroni调和均值(Weighted Bonferroni Harmonic Mean,WBHM)，WBHM同样具有优良性质即幂等性、单调性、可交换性和有界性.

1.2 梯形直觉模糊数的定义与代数运算

自Atanassov提出直觉模糊集(Intuitionistic Fuzzy Set,IFS)以来，因IFS综合考虑了隶属度、非隶属度和犹豫度三方面的信息，从而能更加细腻地描述和刻画客观世界的模糊性本质，众多学者对IFS进行了深入研究[6-9].模糊数表示不确定的量化问题有明显优势，而作为模糊数的推广即直觉模糊数可以更好地表示模糊的内涵.文献[10]给出了三角直觉模糊数的定义.

定义4 集合A为含参变量a1,a,b,c,d,d1的梯形直觉模糊数(Trapezoidal Intuitionistic Fuzzy Number，TrIFN)为实数集R上的集合，记作A={([a,b,c,d];ωA),([a1,b,c,d1];uA)}，其隶属度和非隶属度定义如下：

(4)

(5)

式中,ωA,uA分别表示隶属度的最大度和非隶属度的最小度，且满足条件:

0≤ωA≤1,0≤uA≤1,0≤ωA+uA≤1.

设πA(x)为表示x属于A的犹豫度,且πA(x)=1-μA(x)-vA(x).为了讨论的简洁性，取[a,b,c,d]=[a1,b,c,d1],则TrIFNA表示为A=([a,b,c,d];ω1,uA).当b=c时,TrIFN退化为三角直觉模糊数.

定义5[11]设A1=([a1,b1,c1,d1];ωA1,uA1),A2=([a2,b2,c2,d2];ωA2,uA2)为TrIFNs,λ>0,TrIFN的运算定义如下:

(1)A1⊕A2=([a1+a2,b1+b2,c1+c2,d1+d2];ωA1∧ωA2,uA1∨uA2),其中“∧”“∨”分别表示取大取小算子;

(2)A1⊗A2=([a1a2,b1b2,c1c2,d1d2];ωA1∧ωA2,uA1∨uA2);

(3)λA1=([λa1,λb1,λc1,λd1];ωA1,uA1);

定义6[12]TrIFNA=([a,b,c,d];ωA,uA)的α-割集定义为A(α)={x|μA(x)≥α},0≤α≤ωA.

由式(4)和定义6,α-割集是一个闭区间记作A(α)=[AL(α),AU(α)],

(6)

定义7[12]TrIFNA=([a,b,c,d];ωA,uA)的β-割集定义为A(β)={x|μA(x)≤β},0≤uA≤β≤1.

由式(5)和定义7,β-割集也是一个闭区间记作A(β)=[AL(β),AU(β)],

(7)

2 梯形直觉模糊数的排序

利用(α,β)-割集进行梯形模糊数的排序.文献[13]给出了区间数的排序问题，设a=[aL,aU],b=[bL,bU]为任意给定的区间数，且aL≤aU,bL≤bU.若aL=aU,则区间数退化为一个实数a′,即a′=aL=aU.

定义8 设a,b为任意实数,则a>b的可能度定义为:

(8)

定义9 设a=[aL,aU],a=[bL,bU]为任意实数,则a≥b的可能度定义如下为:

(9)

3 加权梯形直觉模糊Bonferroni调和均值算子

由TrIFBHM的加权形式，提出基于加权TrIFBHM的综合评价问题.

(10)

称WTrIFBHMp，q为加权梯形直觉模糊数Bonferroni调和均值(Weighted Trapezoidal Intuitionistic Fuzzy Bonferroni Harmonic Mean),由梯形模糊数运算律式(1)～式(4),可得定理1.

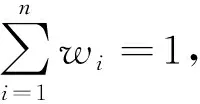
WTrIFBHMp,q(A1,A2,…,An)=

(11)

由WTrIFBHM的定义易知，WTrIFBHM具有幂等性、可交换性和单调性：

性质1(幂等性)若Ai(i=1,2,…,n)均相等,即Ai=A=([a,b,c,d],ωA,uA),则

WTrIFBHMp,q(A1,A2,…,An)=WTrIFBHMp,q(A,A,…,A)=A.

(12)

(13)

(14)

由性质1与性质3易知，WTrIFBHM具备有界性即性质4：

性质4(有界性)设Ai=([ai,bi,ci,di],ωAi,uAi),(i=1,2,…,n)为TrIFNs集.记A-=([∧iai,∧ibi,∧ici,∧idi],∧iωAi,∨iuAi),A+=([∨iai,∨ibi,∨ici,∨idi],∨iωAi,∧iuAi),则

A-≤WTrIFBHMp,q(A1,A2,…,An)≤A+.

(15)

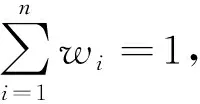
(16)

Aσ(i)=([aσ(i),bσ(i),cσ(i),dσ(i)],ωAσ(i),uAσ(i)),(i=1,2,…,n),(σ(1),σ(2),…,σ(n))是(1,2,…,n)的一个全排列,使得Aσ(i-1)≥Aσ(i),(1,2,…,n).

4 梯形直觉模糊信息下的多指标综合评价

4.1 基于WTrIFBHM的综合评价方法步骤

下面给出基于加权三角直觉模糊数的综合评价问题，具体步骤如下：

步骤1:构造专家评价矩阵Dt.

步骤2:利用集成算子Ai=WTrIFBHMp,q(Ai1,Ai2,…,Aim),计算综合评价值.

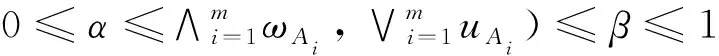
步骤4:计算Ai(λ)

(17)

其中，λ可以反映决策者关于隶属度及非隶属度的偏好水平(λ∈[0,1]).

步骤5:构造判断矩阵P

P=(pij)m×m,

(18)

其中,由式(9)计算pij=p(Ai≥Aj)=p(Ai(λ)≥Aj(λ)),1≤i≤m,1≤j≤m.

步骤6:计算Ai(i=1,2,…,m)的排序指数RI(Ai)[13]

(19)

步骤7:根据RI(Ai)(i=1,2,…,m)对TrIFNsAi(i=1,2,…,m)进行排序.

4.2 应用实例

考虑对某省份甲、乙、丙、丁4个跨境电商部分区域发展水平进行评价，设评价对象集为O={o1,o2,o3,o4},o1,o2,o3,o4分别代表甲、乙、丙、丁4个区域.根据所构建的跨境电商区域发展水平评价指标体系构建属性集C={C1,C2,C3,C4}：C1表示跨境电商物流发展水平；C2表示跨境电子支付发展水平；C3表示电子通关发展水平；C4表示跨境电商基础设施与环境支持水平.其指标权重分别为w=(0.23,0.20,0.27,0.30)T(指标权重可以采用主客观组合赋权法可得，算例中指标权重利用基于最小二乘的AHP-信息熵组合方法得到).现有4个跨境电商专家D={D1,D2,D3,D4}，专家权重分配为η=(0.25,0.25,0.25,0.25)T，4位专家对4个城市的电子商务发展水平进行评价，结果如表1～表4所示.利用研究提出的WTrIFBHM方法，对专家评价矩阵进行计算(Microsoft Windows 10操作系统和AMD A8-7100 Radeon R5，Core 4C+4 G 1.80 GHz 4.0 GB计算机环境下，利用Matlab R2012b实现)．

表1 专家D1给出的评价矩阵A(1)

表2 专家D2给出的评价矩阵A(2)

表3 专家D3给出的评价矩阵A(3)

表4 专家D4给出的评价矩阵A(4)

(1)首先输入规范决策矩阵A(k)(k=1,2,3,4)与指标权重；

(3)利用专家权重向量η，计算得到综合评价值如下：

A1=([0.18,0.28,0.37,0.50];0.5,0.5),A2=([0.22,0.30,0.37,0.45];0.5,0.4),

A3=([0.17,0.29,0.38,0.47];0.5,0.4),A4=([0.20,0.36,0.46,0.54];0.5,0.5).

(4)计算排序等级指数RI(Ai)(取α=β=λ=0.5)，

RI(A1)=0.191,RI(A2)=0.205,RI(A3)=0.199,RI(A4)=0.328.

即o1≻o2≻o3≻o4.利用研究中方法的排序结果表明：区域丁属于该省跨境电商发展的主力,区域乙次之，区域丙与区域甲的跨境电商发展尚处于起步阶段.

5 结束语

针对跨境电子商务发展趋势，提出了跨境电子商务发展的水平评价，并运用直觉模糊集处理评价的模糊性和不确定性，采用直觉模糊多属性群决策方法对跨境电商区域发展水平进行评价.对某省份部分区域跨境电子商务的发展水平进行评价，评价结果对该省跨境电商发展有一定的参考价值.研究在BM算子的基础上，提出了TrIFBHM，WTrIFBHM和WTrIFOBHM等算子，探讨了各算子的优良性质.这些算子适用于处理准则和专家的权重系数均已知，专家给出的备选方案对决策准则的属性权重为梯形模糊数的模糊多准则群决策问题.该方法的主要特点在于考虑了综合评价指标间的关联性，使评价结果更接近实际问题的情况，评价结果更加合理；可操作性强，该方法除了需要通过主客观赋权方法对指标进行赋权,其他程序都可以通过计算机实现.在保证评价专家具有代表性的前提下，可应用于规模较大的企业或政府部门的业绩评价等领域.

结合Bonferroni均值直觉模糊评价方法，采用多个评价主体参与评价，可以提高群组评价的准确性和有效性,是非常有意义的.如何通过对群组评价结果的系统记录，增强组织者选择评价专家的科学性，还有待于进一步研究.