基于主、被动混合模式的柔性薄板振动抑制的控制位置设计

王靖安，王 海

(安徽工程大学 机械与汽车工程学院，安徽 芜湖 241000)

薄板结构在各种工程领域中都有着广泛的应用，但由于其自身结构特性，薄板非常容易产生振动.因此，在薄板的实际工程应用中，首先要解决的问题是对薄板进行抑振.薄板结构的振动抑制方法常用的有主动方法和被动方法两种.被动抑振方法主要通过改变结构的形状，在结构上设置加强筋以及粘贴阻尼片等方式来实现；主动抑振方法主要采用电化学方法、形状记忆合金方法以及压电陶瓷方法来实现.被动抑振措施针对较高频率的振动有着良好的抑制效果，但是对于低频振动的抑振效果不佳；主动抑振措施的抑振范围较广，但是需要消耗较多的能量.如果将主动抑振方法和被动抑振方法结合，则有望实现在消耗较少能量的条件下，实现对高、低频范围振动的有效抑制.

刘鸿文[1]总结和阐述了关于板壳的基本概念与基本理论，并介绍了关于矩形板的数学解法和基于能量原理的解法.Marco Amabili[2]主要提出了关于弹性板的非线性振动理论.Marian[3]针对随机激励结构系统，提出了基于调谐质量阻尼器的被动抑振方法.汪艳霞[4]综述了在建筑设计中的主动、被动以及主被动结合的振动控制方法.Bodaghi[5]针对板结构，采用有限元的方法，利用形状记忆合金对板的振动进行被动控制.Ferrari[6]利用弹性绳将一块矩形板的四角吊起挂在一个框架中，模拟四边简支的条件进行复合层板的抑振实验研究.王海[7]针对悬臂梁结构，使用压电片对梁的振动进行主动抑制，并通过仿真和实验，确定压电片的最佳粘贴位置.Araujo[8]采用有限元方法，针对各向异性层合夹层结构，构建了主、被动混合阻尼的模型.Plattenburg[9]针对一个粘贴有主动压电片和被动阻尼片的矩形薄板，采用瑞利-利兹法，构建了解析模型，并通过实验验证解析模型的准确性.

针对上述研究中存在的问题，同时考虑在尽量减少能耗的条件下达到对振动的有效抑制，提出了主、被动混合模式的振动抑制方法，把薄板等面积分成3×3共计9块位置，通过在不同位置分别粘贴阻尼片和压电片，对薄板的振动进行抑制.

1 矩形板建模及其抑振器设计

在实际工程应用中，薄板结构主要以矩形板为主.总体示意图如图1所示.将薄板结构简化成一块尺寸为600 mm×400 mm×1.2 mm的矩形板进行分析，在矩形板上不同位置粘贴阻尼片和压电片，对矩形板的振动进行抑制.

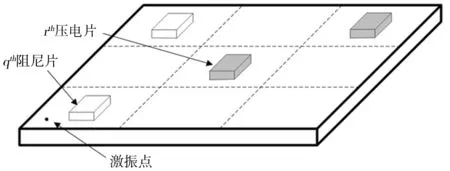
图1 总体示意图

基于Kirchhoff薄板理论对矩形板进行建模，通过几何关系和力平衡关系，可以得到矩形板横向自由振动的微分方程：

(1)

该微分方程的解可以表示为：

w(x,y,t)=W(x,y)sin(ωt+φ)，

(2)

将式(2)代入式(1)中，可得：

(3)

式中，

(4)

设置矩形板的长和宽分别为a和b，边界条件为四边简支，表示为：

(5)

满足该边界条件的振型解可以表示为：

(6)

式中，A为常数.

将式(6)代入式(3)，可得四边简支矩形板的第(m,n)阶固有频率：

(7)

如图1所示，假设矩形板上共粘贴有Np块阻尼片，则阻尼片和矩形板的运动分别可用下面的广义位移矢量ri表示：

(8)

式中,u、v、w分别表示矩形板在X、Y、Z3个方向上的位移，Ψxz、Ψyz分别表示矩形板在XZ、YZ面内的转角.

假设该广义位移矢量可以记成Ns个形函数的加权求和：

(9)

该阻尼板的动能和势能分别可以写成：

(10)

式中,M是质量矩阵，K是刚度矩阵，如式(11)所示：

(11)

在矩形板(xd,yd)位置施加一点激励Fd：

Fd(x,y,t)=Fdδ(x-xd)δ(y-yd)ej(ωt+θd),

(12)

式中,θd表示激励信号的相位.

如图1所示，假设在矩形板上共粘贴有Nc块压电片，矩形压电片对矩形板所施加的力可以等效成横向偶极力[10]：

(13)

式中,θc表示激励信号的相位，δ表示狄拉克δ函数，H表示海维赛德函数，M表示力矩，具体表示如式(14)所示：

(14)

针对上述各式使用拉格朗日方程，得到：

(15)

进而得到矩形板的稳态响应矢量：

q(ω)=[K(ω)-ω2M]-1[Fd+Fc],

(16)

2 抑振策略分析

根据振动理论可知，在振源附近位置和矩形板模态应变最大位置进行抑振会得到较好的抑振效果.通过在矩形板上粘贴阻尼片，增加局部阻尼，对矩形板的振动进行被动抑制；通过在矩形板上粘贴压电片，利用逆压电效应，给压电片施加合适的电压，产生与矩形板振动方向相反的形变，对矩形板的振动进行主动抑制.

如图1所示，为了便于描述在矩形板上粘贴阻尼片和压电片的位置，把矩形板等面积分成3×3共计9块位置.为了模拟外界干扰对矩形板的影响，在矩形板左下角(50，50)位置施加一正弦点激励.

碳纤维矩形板、丁基橡胶阻尼片和PZT-5H压电片的参数如表1所示.

表1 矩形板、阻尼片和压电片参数

使用COMSOL软件进行仿真，COMSOL是一款多物理场耦合有限元软件，对矩形板做模态分析，得到矩形板前三阶模态振型，其振型图如图2所示.由图2可知，在一阶模态下，矩形板正中央位置的应变最大；二阶模态下，矩形板沿着长度方向两边位置的应变最大；三阶模态下，矩形板沿着宽度方向两边位置的应变最大.因此设计如图3所示抑振方案，分别抑制该矩形板的前三阶振动.左下角的点表示激振点，在激振点处施加幅值为1mm,频率分别为142.66 Hz，220.56 Hz，350.96 Hz的三种点位移信号，模拟矩形板的前三阶振动，图中黑色方块位置表示该阶振动下，矩形板模态应变最大位置，白色方块位置表示激振处附近位置.

图2 矩形板前三阶模态振型

图3 抑振方案示意图

设计如下3组仿真来进行对比：①仅给矩形板施加一正弦点激励，不加任何控制；②给板施加一正弦点激励，采用纯被动控制方法，在激振点附近位置和模态应变最大位置分别贴上一块阻尼片，来达到抑振的效果；③给板施加一正弦点激励，采用主、被动混合模式控制方法，在激振点附近位置粘贴阻尼片，在模态应变最大位置粘贴压电片，并给压电片一个幅值为70 V，频率与正弦点激励频率相同、相位相差180°的正弦电压信号，来产生与矩形板振动方向相反的形变，从而达到抑振的效果.

在矩形板模态应变最大位置附近，避开所粘贴的阻尼片或者压电片，确定一点作为测量点，测量其沿Z轴方向位移，另外测量整个矩形板的动能，以这两个数据作为依据来判断抑振效果.把第i个方案的抑振率定义如下[7]：

(17)

式中，ED是矩形板模态应变最大位置附近一点的横向位移的抑制率；EK是整个矩形板的动能的抑制率；N表示所绘制的位移和动能曲线图的峰值的个数；pi0表示不施加任何控制时，每个峰值的大小；pij表示施加控制后，每个峰值的大小.

3 COMSOL仿真结果

矩形板一阶振动下的抑振结果如图4所示.在矩形板一阶振动模式下，图4a表示不加任何控制和纯被动控制两种情况下，模态应变最大位置附近一点沿Z方向的位移大小的对比；图4b表示纯被动控制和主、被动混合模式控制两种情况下，模态应变最大位置附近一点沿Z方向的位移大小的对比；图4c表示不加任何控制和纯被动控制两种情况下，整个矩形板总动能大小的对比；图4d表示纯被动控制和主、被动混合模式控制两种情况下，整个矩形板总动能大小的对比.经数据处理后，可以得到如下结果：在纯被动控制下，对模态应变最大位置附近一点的位移的抑振率为26.12%，矩形板总动能的抑振率为48.27%，综合抑振率为37.195%；在主、被动混合模式控制下，对模态应变最大位置附近一点的位移的抑振率为66.75%，矩形板总动能的抑振率为82.11%，综合抑振率为74.43%.

矩形板二阶振动下的抑振结果如图5所示，在矩形板二阶振动模式以及纯被动控制下，对模态应变最大位置附近一点的位移的抑振率为28.88%，矩形板总动能的抑振率为52.88%，综合抑振率为40.88%；在主、被动混合模式控制下，对模态应变最大位置附近一点的位移的抑振率为60.44%，矩形板总动能的抑振率为74.92%，综合抑振率为67.68%.

矩形板三阶振动下的抑振结果如图6所示，在矩形板三阶振动模式以及纯被动控制下，对模态应变最大位置附近一点的位移的抑振率为15.39%，矩形板总动能的抑振率为7.4%，综合抑振率为11.395%；在主、被动混合模式控制下，对模态应变最大位置附近一点的位移的抑振率为28.37%，矩形板总动能的抑振率为20.42%，综合抑振率为24.395%.

将不同阶振动模式以及不同控制方法下的抑振率总结如表2所示.由表2可以看出，经过控制，矩形板的振动得到了一定的抑制，另外，主、被动混合模式控制下的抑振率明显高于纯被动控制下的抑振率.因此，主、被动混合模式控制相对于纯被动控制，对于矩形板的振动会有更好的抑制效果.

表2 矩形板前三阶振动模式下的抑振率

图4 矩形板一阶振动下的抑振结果

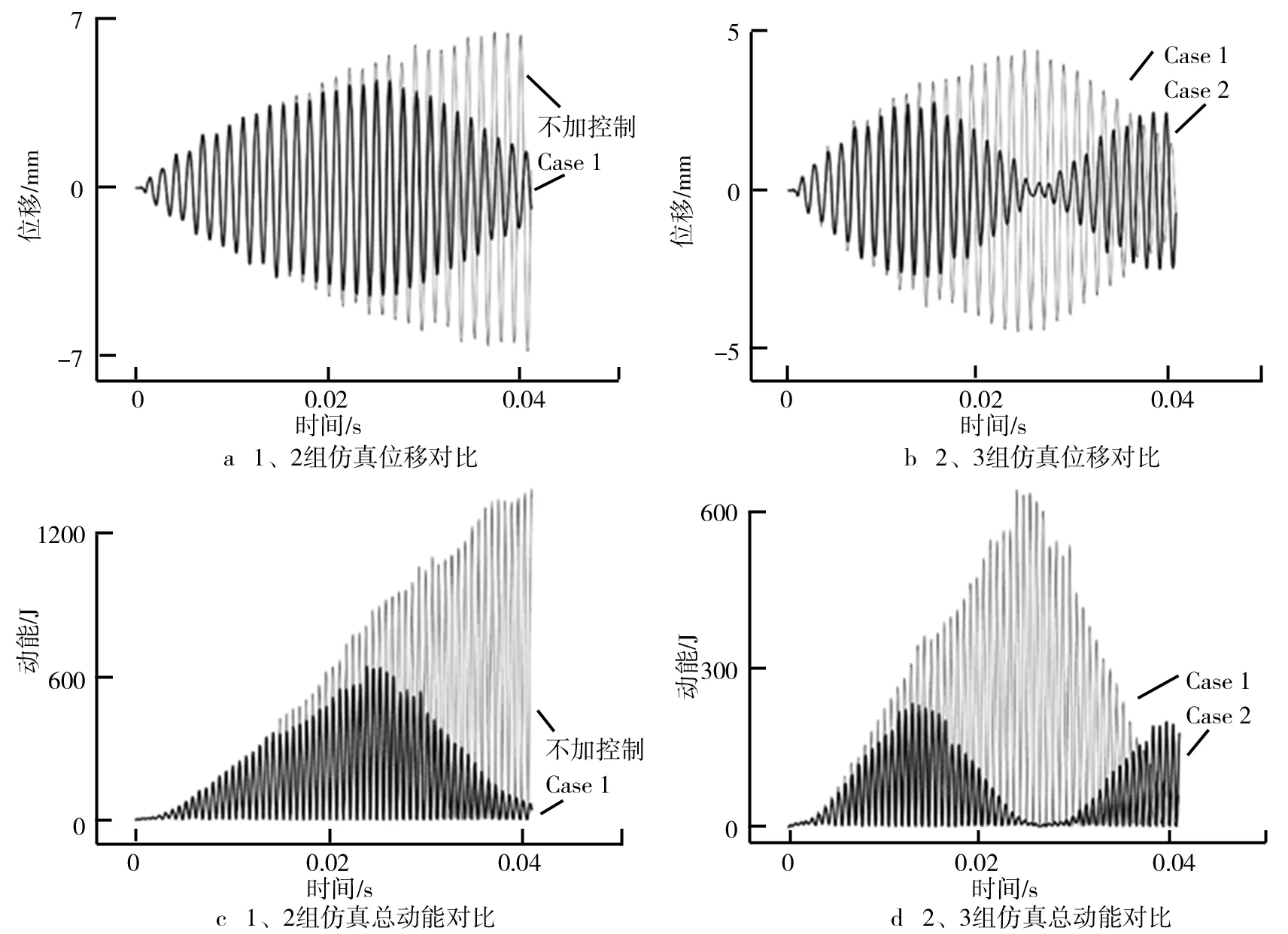
图5 矩形板二阶振动下的抑振结果

图6 矩形板三阶振动下的抑振结果

4 结论

文章主要研究关于矩形板的振动的抑制策略，通过在激振处附近位置和模态应变最大位置粘贴阻尼片和压电片，进行被动和主动控制.通过对前三阶振动模式下的3组仿真的对比，可以得到结论：主、被动混合模式控制相对于纯被动控制，抑振率分别增加了37.235%、26.8%和13%，对于矩形板的振动会有更好的抑制效果.后期，将在此结论的基础上进行更进一步研究，研究施加在压电片上的正弦电压信号的幅值和相位对抑振效果的影响，另外，参考仿真模型，搭建实验平台，来验证仿真结果的准确性.