浅谈培养初中生如何进行数学解题反思
2018-11-29马仕红
马仕红


数学学习的过程与数学解题息息相关,但数学思维的培养提高并不在于数学解题的数量,而在于数学解题的质量,所以我们应该注重解题过程中方向的明确、策略与技巧的正确应用,在数学解题的过程中不断总结经验,积累解题的思维方法,不断提高数学解题的能力,对于已经解决的数学问题,我们要回过头来进行反思:反思对题意的理解;反思对思维方式和知识点的运用;反思技能和技巧的运用,在对整个解题过程的回顾中发现问题、提出问题,这样可以培养学生质疑问难、举一反三的能力,这对发展学生的创新性数学思维能力至关重要.
1 如何培养学生进行解题反思
在实际教学过程中,学生认为解题反思就是叙述解题过程,能说出解题思路,其实这仅仅停留在反思的表面,因而在教学过程中如何培养学生进行解题反思、所谓的解题反思到底要反思些什么就显得尤为重要,以下结合笔者的教学实践,从几个方面谈谈如何培养学生解题反思能力.
1.1 反思解题过程中的问题本质,做到举一反三
在数学解题中如果能做到“当你看见树木就能想象到一片森林”的境界,那么学习数学就会轻松很多,也就是如果你能通过会做一道题而会做一类题,做到真正的举一反三,数学思维自然而然得到提升,
例1 如图1,点B,C在线段AD上,问:图中共有几条线段?是哪几条?
问题1 往返于A,B两个城市的火车有四个停靠点,问:(1)该火车有多少种不同的车票?(2)该火车上要准备多少种车票?
问题2 数一数,图2中共有多少个三角形?利用所标字母,将它们表示出来,
反思 问题1实际考查线段的定义,由于票价随着路程的长短而变化,所以线段数就是票价数,而问题二中的三角形的个数实际上也可以这样来看,点C,D在线段B上,共有几条线段,这样问题转化后就变得简单许多,学生做题的正确率也大大提升.
数学问题往往以不同形式呈现,但问题解决后要发现其中的“奥妙”,要让学生学会“透过现象看本质”,架起数学问题的形式与问题本质之间的联系,不要再停留在题目的表面,要努力看清其庐山真面目,在遇到形异质同的题目时能迅速地识别.
1.2 反思解题过程中的做题方法,优化解题方式
所谓“条条大路通罗马”,虽然目的地都一样,但是时间短者应该有更大的收获,正如在数学解题时一样,同样的一道题目,不同的学生可能有不同的方法,在解答正确的前提下,选择最简便方法的学生不论在平时的练习中还是考试中都很有利,此时学生就要反思自己的思路和学生的思路以及老师的思路有什么不同?差距在哪里?造成这差距的原因在哪里?我该如何来改进?
坚持这样的反思,不仅收获更多的解题方法,解题思路也会进一步被打开,在以后的数学学习及解题过程中也会游刃有佘,
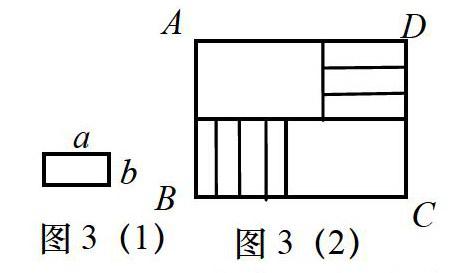
例2 用7张如图3 (1)所示的长为以,宽为6(a>b)的小长方形纸片,按图3(2)所示的放置方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示,设左上角与右下角阴影部分的面积之差为S,当BC的长度变化时,按照同样的放置方式摆放,S始终保持不变,则a,b应满足的数量关系为____.
学生拿到此类题目肯定觉得头疼,无从下手,但仔细阅读题目关键词句:“当BC的长度变化时,S始终保持不变”后,仔细想一想,是不是与“(x+1)(2x2+ax+1)的计算结果中不含x2的项”有异曲同工之处,只要将多项式乘以多项式展开,将x2项前面的系数令为0即可,根据这样的思路,我们将S表示成关于BC的形式,由题意有S=S1-S2=(BC·3b-3ab)-(BC·a-4ab).将S表示出来后,由于BC变化对S没有影响,则3b-a=0,从而找到a=3b这样的数量关系,分析从读题、思考、解题的这一系列的过程,我们发现,如果能很好地进行知识的类比,优化解题的方式,那么数学解题就会变得很轻松.
1.3 反思解题过程中的易错点,打破思维定势
例3 某課外活动小组中男生人数占全组人数的一半,如果减少6名男生,那么男生人数就占全组人数的1/3,求这个课外小组的人数.
错解 设这个课外小组有x人.
答:这个课外小组有36人.
1.4 反思解题过程中的拓展延伸,培养创新意识
反思解题过程时,如果就题论题,那么这种反思似乎只停留在表面,教师应培养学生这样的意识,多问自己以下几个问题:
(1)这题是否可以一题多解,这几种解法之间是否存在着某种本质上的联系?
(2)根据所学知识,以及知识点间的联系,问问自己如果改变题目中的某一个条件能否用相同的解题思路,得出的结论还一样吗?或者结论之间有什么联系吗?
(3)能否将问题进行拓展或者推广?
例4 已知:如图4,△ABC中∠B与∠C的平分线相交于点P,
(1)试探索若∠ABC+∠ACB= 100°,求∠BPC的度数.
(2)若∠A=80°,求∠BPC的度数.
(3)试说明∠A与∠BPC的关系.
法1 利用三角形的内角和与平分线的性质,我们可以直接求出.
法2 连接AP并延长与BC交于点D,利用三角形外角和性质可以求出∠BPC等于∠A与∠ABP与∠ACP和,再利用角平分线性质可以知道∠ABP与∠ACP的和等于∠ABP与∠ACP和的一半.
问题变式 变式1 如图5,BP,CP分别平分∠DBC与∠ECB,试探索∠A与∠P的数量关系.
例题中的∠P是由三角形的两个内角的角平分线构成,而变式1中的∠P是由三角形的两个外角平分线构成的,探索∠P与∠A关系的思路还是一样的吗?或者有什么不一样的地方?
变式2 如图6,BP,CP分别平分∠ABC与∠ACD,试探索∠A与∠P的数量关系.
不同于例题以及变式1,∠P既不是由两个内角平分线构成也不是由两个外角平分线构成,而是由一个内角平分线与三角形的一个外角平分线构成,在探索的过程中又需要什么新的知识点?
通过这样的变式,不仅学生的思维能得到发散,在长期的潜移默化中,学生在遇到一些问题时能自然而然地多问自己几个问题,对题目进行简单的变式,久而久之学生能在数学解题中找到乐趣.
问题拓展如图7,在四边形ABCD中,∠DAB的角平分线与∠ABC的外角平分线相交于点P,且∠D+∠C= 240°,则∠P=____.
研究多边形的外角时,教学过程中主要是以三角形为主,那当三角形改成任意的四边形时,我们还能得到相类似的结论吗?
2 结语
“磨刀不误砍柴工”,解题反思就是我们手中的那把砍柴刀,解题反思是提高数学学习能力的有力手段,在反思过程中不断地学会挖掘题目的本质,在寻找更好的解题方法的过程中发展思维,当然,解题反思不是一蹴而就的,教师要在日常的教学中有针对性地利用习题,让学生学会反思,在学中反思,在反思中学,让学生不再把解题当做一种任务,而是变成一种有目标,有研究性、探究性的学习活动,在这样的一个过程中学会解题,学会数学学习.
参考文献
[1][美]波利亚著,阎育苏译.怎样解题[M].北京:科学出版社,1982
[2]汤炳兴,叶红著.中学数学解题学习[M].北京:化学工业出版社, 2010
[3]高鹏.透过现象看本质兼谈数学解题反思[J].中学数学教学参考,2008 (11):32-34
[4]靳莉颖.数学解题反思能力的培养[J].现代教育科学,2011(6):127-127
[5]刘良聪.数学解题反思与思维能力的培养[J].吉林教育,2008 (2):90-90
