依托推理型试题 考查推理能力

林湧 胡鹏程

以合情推理或演绎推理能力为主要考查目标的“推理型”试题，在中考数学试卷中有着不可替代的地位.2017年福建省中考卷较为合理地借助推理型试题，全面地考查了学生的推理能力，本文拟对该试卷中的推理型试题的做归类分析，并借此谈谈对此类试题的一些思考.

1 推理型试题的分类剖析

推理型试题的基本模型是：推理性结果=f（情境，对象，条件，推理性任务），情境、对象、条件、推理性任务这四大要素是试题的四个变量，f则反映了这四大要素之间的结构关系，根据试题模型中任务要素的不同思维特征，又可以将推理型试题大致分为合情推理型试题、说理推理型试题、综合推理型试题三类.

1.1 合情推理型试题

合情推理与演绎推理是相辅相成的两种推理形式，推理型试题理所自然派生出以合情推理能力为主要考查目标的一类，合情推理型试题所蕴含的思维方式主要有归纳、类比、空间想象、统计推断等，

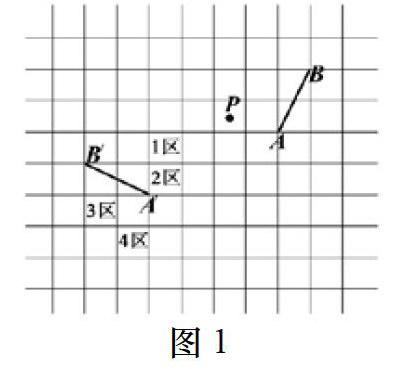
例1（2017年福建省中考试卷·10）如图1，网格纸上正方形小格的边长为1，图中线段AB和点P绕着同一个点作相同的旋转，分别得到线段A'B'和点P'，则点P'所在的单位正方形区域是

A.1区

B.2区

C.3区

D.4区

本例以网格图为背景设计问题，以空间想象为主导性思维，同时也都包含了一定的分析性思维，此类试题不必精确计算或严格论证，只需“大致”作出判断，合情推理即可，随便指出，学生由于思维水平的差异容易产生不同的结果，利用这些结果设计干扰项有助于提高试题的信度，根据所选择的结果在一定程度上可以推断正确解答的学生均具有相同的学业水平，因此本题使用选择题型是适宜的.

1.2 说理推理型试题

说理推理，不单指严格意义上的证明，它还可以采用严格证明以外的其它说理方式，根据说理的方式不同，说理推理型试题又可进一步分为：逻辑推理形式的推理型试题、分析为主的推理型试题和基于计算的说理推理型试题，

例2（2017年福建省中考试卷·18）如图2，点B，E，C，F在一条直线上，AB=DE，AC=DF，BE=CF，求证：∠A=∠D.

本题以三角形为基本图形，在多组线段相等条件下，设置了等角的证明问题，这是典型的逻辑推理形式的推理型试题，能较好地考查学生的逻辑推理能力，基于此类试题能考查严格形式逻辑推理的能力，绝大多数试卷对此都有所涉及，这也反映了数学教育与评价的必然要求.

例3（2017年福建省中考试卷·15）两个完全相同的正五边形都有一条边在直线l上，且有一个公共顶点O，其摆放方式如图3，则∠AOB等于____度.

例3属于分析为主的推理型试题，与例2的严格推理书写所不同的是，此类试题的分析主要发生在头脑中而不必用文字表述出来，从题型上来看，此类试题一般以填空或选择的形式出现，

例4（2017年福建省中考试卷·23）自2016年国庆后，许多高校均投放了使用手机就可随取随用的共享单车，某运营商为提高其经营的A品牌共享单车的市场占有率，准备对收费做如下调整：一天中，同一个人第一次使用的车费按0.5元收取，每增加一次，当次车费就比上次车费减少0.1元，第6次开始，当次用车免费，具体收费标准如下：

同时，就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿，得到如下数据：

（1）写出a，b的值;

（2）已知该校有5000名师生，且A品牌共享单车投放该校一天的费用为5800元，试估计：收费调整后，此运营商在该校投放A品牌共享单车能否获利？说明理由.

本题以具有时代气息的“共享单车”构成新颖的问题情境，以表格的形式给出数据，更蕴含了能考查学生的阅读能力、数据分析观念，对于问题“运营商在该校投放A品牌共享单车能否获利”，必需建立在计算的基础上进行推理，所以此类题目属于基于计算的说理推理型试题.

1.3 综合推理型试题

所谓综合推理型试题，是指试题中既涉及合情推理，又涉及逻辑推理的说理，或者包含了不同的说理方式，

例5（2017年福建省中考试卷·22）小明在某次作业中得到如下结果：

（1）当α=30°时，验证sin²α+sin²（90°-α）=1是否成立;

（2）小明的猜想是否成立？若成立，请给予证明;若不成立，请举出一个反例.

本题的构造方式是：先给出5组算式，在此基础上，提出一般性情形的猜想，对于猜想又采用先取特殊值验证再一般化证明的形式，这是一个由具体数值计算到符号公式表达的过程，这样的问题，包含了特殊情形下的分析推理，由特殊到一般的猜想，以及严格的逻辑证明，由此可由不同的推理方式考查学生不同层次、不同侧面的推理能力.

2 关于推理型试题的思考

2.1 推理型试题的价值

推理在数学中具有重要的地位，《义务教育数学课程标准（2011年版）》指出：“推理是数学的基本思维方式，也是人们学习和生活中经常使用的思维方式，”推理能力是评价学生数学素养的一项重要指标，也是数学课程和课堂教学的重要目标，基于解题是评价的一个重要途径，所以考试中命制推理型试题既是对学生推理能力的有效考查，也在一定程度上对教师教学目标的达成情况形成检验.

像中考这种大规模的带有较为明显选拔意图的考试，其试题的价值已经大大超越了对知识或技能的考查，它对教学具有很强的导向性，如例5作为一道综合推理型试题，既考查演绎推理能力又兼顾合情推理，势必对日常的教学产生正向的影响，如果在教学过程中重演绎，轻归纳、类比，只满足于证明现成结论，学生较少經历探索结论、提出猜想的活动过程，就可能导致其合情推理能力弱于演绎推理能力，而实际上，作为推理的两种形式，合情推理与演绎推理必须协调发展，甚至可以说在数学中发现结论比证明结论更有价值，

需要指出的是，例5所证明的“同一个角的正弦平方、余弦平方之和等于1”虽然是后续的高中学习的内容，但本题只是选取了这样一个素材进行探究，一线教师应该充分理解命题者意图，不可在今后的教学过程中随意补充、扩充教学内容，更不可将后续的学习内容简单下放.

2.2 推理型试题的题型运用方式

考查目标对题型的使用有着举足轻重的作用，试题所蕴含的可能考查功能、命题者所希望达成的考查目标与题型使用的关系有一定的规律可循，一般情况下，如果侧重考查对概念理解、对空间图形的直观把握以及简单的推理分析、归纳性的合情推理，使用选择题型或填空题型设计试题较为适宜;如果以学生的推理论证能力、说理能力、综合分析探究能力为重点考查目标，解答题型则是首选，就单个试题而言，由问题到试题有题型的使用问题，就一份试卷而言，还需要考虑各相关试题的题型配合使用问题，

试题中问题任务的类型与题型的使用有着内在的关联，对于论证、探究、求解等任务，因其具有较为突出地考查学生的相关能力或品质的功能，一般来说设计为解答题型试题显得较为自然;对于猜想、判断等任务，则需兼顾情境的复杂性、整卷的题型搭配及命题者的思维习惯等方面的因素选用不同的题型设计试题，

从某种意义上说，大部分试题都包含了一定程度的推理，而推理的步长、推理的类型与题型的使用也存在一定的关联，推理步长不长、属于合情推理的题目，通常情况下可考虑采用填空题或选择题;而推理步长较长、属于逻辑推理论证之类的题目宜使用解答题型设计试题.