双旋弹道修正弹弹体非对称载荷的数值研究
2018-11-29冯斌于纪言鞠潭王晓鸣王钰
冯斌, 于纪言, 鞠潭, 王晓鸣, 王钰
(南京理工大学 智能弹药技术国防重点学科实验室, 江苏 南京 210094)
0 引言
固定鸭舵双旋弹道修正弹是一种由传统旋转稳定弹体加装固定鸭舵修正组件(见图1)而成的低成本有控弹药。固定鸭舵修正组件的差动舵斜置方向相反,操纵舵斜置方向相同,总体呈非对称布局,因此鸭舵产生的非对称涡系会对弹体诱导产生非对称载荷,尤其在垂直于攻角平面的方向具有侧向力。
目前国内研究中,程杰等[1]建立了双旋弹道修正弹气动力工程模型并辨识了相关参数;纪秀玲等[2]通过数值计算,得出双旋弹道修正弹鸭舵相位角和全弹法向力、俯仰力矩变化呈三角函数关系的结论;许安勇[3]通过数值研究计算了双旋弹道修正弹弹丸各修正状态的稳定因子,得出弹丸各修正状态均具有良好飞行稳定性的结论。
国外对于双旋弹道修正弹鸭舵与后体相互作用进行了一些研究。Silton等提出高机动性导弹(HMA)的结构[4],使用计算流体力学(CFD)方法对导弹各部分的气动力系数进行了研究[5];Coyle等[6]使用嵌套网格对HMA进行CFD计算,研究了其气动特性;Silton等[7]研究了HMA的滚转特性,发现双旋弹道修正弹鸭舵洗流对HMA尾翼有明显影响;Elkins等[8]通过理论建模,将磁共振测速(MRV)法应用于流体运动的研究中;Wells等[9]使用定常雷诺平均(RANS)法仿真验证了MRV实验结果;Youn等[10]设计了MRV实验和水洞实验来等效低速飞行实验,通过染料将双旋弹道修正弹鸭舵与后体的相互影响可视化;DeSpirito[11]对比使用了剪切压力传输(SST)k-ω湍流模型的CFD数值计算和风洞粒子图像测速(PIV)法实验结果,验证了CFD仿真对双旋弹道修正弹鸭舵尾涡有效捕捉的能力;Dawson等通过实验分析了双旋弹道修正弹弹翼对轴对称弹体的作用效果,发现弹体俯仰、滚转力矩与舵偏角呈线性关系[12],并在超音速时对比了风洞实验和Missile Datcom工程计算的结果,结果表明两种方法的一致性较好[13]。
目前对于固定鸭舵双旋弹道修正弹的研究主要集中在全弹层面,缺少关于非对称鸭舵对弹体诱导产生非对称载荷的研究与建模;而目前关于制导弹箭弹鸭舵对后体干扰的研究重点在鸭舵对尾翼的干扰,缺少非对称鸭舵对回转体弹体的干扰研究。对于研究方法,风洞实验方法中使用的六分量风洞天平虽然能够测得全弹的气动力,但是并不能直接测得鸭舵尾涡和弹体的相互作用,而CFD方法对三维流场细节有良好的捕获能力,可以得到双旋弹道修正弹各个部件的气动力。
本文使用CFD方法复现风洞实验,并对比计算结果与实验数据,验证CFD方法的有效性。使用CFD方法分别对0°、2°和4°舵偏双旋弹道修正弹模型进行计算,通过对多攻角、多马赫数情况下的计算结果进行对比分析,得出弹体非对称载荷与非对称鸭舵的关系,为气动力模型的修正奠定了基础。
1 数值方法验证
本文的研究对象是双旋弹道修正弹固定鸭舵和下游弹体之间的相互作用。下面对CFD方法精确捕捉弹翼尾涡的能力以及准确预测弹体气动力的能力进行验证。
1.1 弹翼尾涡的精确捕捉能力验证
为了验证CFD方法对弹翼尾涡的精确捕捉能力,使用数值计算结果与文献[11]中的实验结果进行对比。在文献[11]的实验中,舵片以一定舵偏角固定于美国Sandia国家实验室三音速风洞中,使用PIV方法对舵片下游不同距离4个截面的速度场进行测量。
1.1.1 验证使用的模型和方法
验证工作使用的计算域为美国Sandia国家实验室三音速风洞的测试段,采用的舵片和风洞底面的网格如图2所示。计算使用有限体积法,入口马赫数为0.8.
1.1.2 结果验证
在舵片下游的流场中,设u为x轴方向速度分量,c为弹翼根弦长,u∞为入口处速度。通过选取4个截面x/c=0.51、x/c=1.18、x/c=2.18和x/c=4.18,绘制归一化横向速度云图,如图3所示。从图3的翼片尾迹中可以明确观测到翼尖涡,并且随着流动衰减。在翼根部尾迹中也可以观测到卷起的壁面附面层。
绘制4个观测截面上过涡核水平线(见图3)上的归一化切向速度(即y轴方向速度分量v比入口速度u∞),并与文献[11]中的实验数据进行对照,如图4所示。由图4(a)~图4(c)可见,CFD计算得到的结果与实验结果吻合一致性非常好;由图4(d)可见,CFD的计算结果表现出了更大的耗散,最大切向速度值略小于实验值,但是仍然有较好的一致性。由此表明CFD方法可以对双旋修正弹弹翼尾涡进行精确捕捉。
1.2 气动力的准确预测能力验证
为了验证CFD方法的气动力预测能力,下面使用CFD方法对前期研究中的双旋弹道修正弹模型进行计算,定量对比计算结果与风洞实验中六分量风洞天平测力数据。
1.2.1 验证使用的模型和方法
首先对双旋弹道修正弹所在计算域进行三维建模和空间离散。图5所示为4°舵偏双旋弹道修正弹计算域网格,计算域按照空间分布,分解为鸭舵绕流区、弹体绕流区和外部流场。将计算域空间离散化,生成全六面体非结构网格。
求解过程使用密度基求解器,对流项使用Roe通量差分格式离散,梯度使用最小二乘法求解,其余流动变量使用2阶迎风格式离散,湍流模型选择SSTk-ω模型。分别计算马赫数为1.5~4.0以及0°攻角条件下4°舵偏的全弹模型阻力、升力系数。
1.2.2 结果验证
数值计算和文献[11]风洞实验得到的阻力系数、升力系数结果对比如图6所示。由图6可见:对于两种气动力系数,计算值和实验值具有相同的变化趋势;阻力系数计算值相对误差小于13%,升力系数计算值相对误差小于12%. 对于工程应用,其相对误差处于可接受范围内,表明CFD方法的气动力预测能力是有效的。
2 鸭舵诱导双旋弹道修正弹弹体非对称载荷的研究
下面对非对称鸭舵双旋弹道修正弹模型进行建模和仿真,并通过对结果的定性和定量分析研究非对称鸭舵对双旋弹道修正弹弹体诱导产生非对称载荷的规律。
2.1 使用的模型和方法
对舵偏分别为0°、2°和4°的双旋弹道修正弹模型进行数值计算,计算条件如表1所示。使用的计算域离散方法、求解器、控制方程离散方法、梯度求解方法和湍流模型均与1.2节相同。

表1 计算条件
2.2 对流场的定性分析
对流场的定性分析在马赫数为0.8条件下进行,以0°和4°攻角情况的计算结果为例,绘制流场中鸭舵尾流的流线图如图7~图12所示。
由图7可见,在0°攻角下,对称模型的4片鸭舵当地攻角都为0°,每片鸭舵的左舷面和右舷面之间没有压力差,因此没有产生旋涡,对弹体并没有产生非对称的影响。由图8可见,在4°攻角下,对称模型只有水平分布的两个操纵舵当地攻角不为0°,且均产生了一对旋涡,但是由于两个操纵舵的当地攻角大小相等,两个涡强度相同且对称,操纵舵对下游弹体的影响是对称的。
0°攻角条件下的非对称模型(2°舵偏模型、4°舵偏模型)如图9、图10所示。由图9、图10可见,4片鸭舵的当地攻角相等,但斜置方向不同。模型水平布置的两片操纵舵呈面对称分布,竖直分布的两片差动舵关于弹轴中心对称,因此两片操纵舵的尾涡呈面对称,两片差动舵的尾涡关于弹轴中心对称,此时4片鸭舵的涡系对弹体作用是不对称的。4°攻角条件下的非对称模型(2°舵偏模型、4°舵偏模型)如图11、图12所示。由图11、图12可见:除了鸭舵非对称偏置的影响,由于攻角存在,位于上方的舵片处于背风侧,其拖出的涡线远离弹体,对弹体影响减弱;位于下方的舵片位于迎风侧,涡线贴近弹体,对弹体影响增强。以上因素的共同作用产生了弹体非对称载荷。
通过观察弹体上表面和下表面的压力系数关于弹轴的对称性,可以定性分析弹体载荷的对称性。提取弹体上表面和下表面的压力系数Cp,并绘制成云图,如图13~图18所示。对于对称模型,在马赫数为0.8、0°攻角(见图13)和4°攻角(见图14)条件下,弹体上表面和下表面的压力系数均对称分布。
对于非对称模型,在马赫数为0.8、0°攻角(见图15、图16)和4°攻角(见图17、图18)条件下,弹体上表面和下表面的压力系数均出现明显的非对称现象。
通过上述对流场的分析可知,鸭舵非对称布局对弹体表面的压力系数分布非对称性有巨大影响。
2.3 对弹体受力定量分析
分析非对称鸭舵对弹体非对称载荷的影响,需要对弹体受力进行定量分析。首先建立弹体坐标系,原点O在全弹质心,x轴与弹轴重合、指向弹尾方向,y轴垂直于x轴、指向上方,z轴与Oxy平面垂直。下面通过对比弹体截面压力系数、弹体法向力系数、侧向力系数,来定量分析弹体载荷的对称性。
2.3.1 弹体压力系数
为了定量比较弹体的压力系数差异,在马赫数为0.8条件下,选择3种模型距弹顶5倍弹径的弹体截面,提取截面所在位置弹体的压力系数并在极坐标系下绘制,如图19、图20所示。
从图19、图20可见:0°舵偏模型在两种攻角下的压力系数均是对称的,而2°舵偏模型与4°舵偏模型在两种攻角下的压力系数均是非对称的;4°舵偏模型的非对称性比2°舵偏模型更加明显。当存在攻角时,弹体的第Ⅳ象限受到迎风侧差动舵片的尾涡影响较大,弹体会在z轴方向产生侧向力。对比截面压力系数图(见图19、图20)的曲线和对应条件的流线图(见图7~图12),观察到鸭舵尾涡扫过的弹体部分压力系数较低。可以使用涡的理论来解释这种现象:翼尖涡在空间中诱导出1个速度,与来流速度矢量叠加,使受涡影响的弹体表面空气流速较快、压力系数较低。
2.3.2 弹体的力系数
弹体非对称载荷直观体现在弹体受力情况,下面根据CFD计算结果数据,分别计算弹体法向力系数Cn和侧向力系数Cz. 通过对弹体法向力系数和侧向力系数分析,定量分析非对称鸭舵对弹体受力影响。
2.3.2.1 法向力系数
弹体受到法向力Fn的方向为坐标系y轴方向,法向力系数计算公式如(1)式所示。
(1)
式中:ρ∞为参考密度;v∞为参考速度;S为参考面积。
以马赫数为0.8时的计算结果为例,绘制-8°~8°攻角下3种模型弹体法向力系数的变化曲线,如图21所示。
从图21中可见,当马赫数为0.8时,3种模型的弹体法向力系数高度重合。以图19和图20中的弹体截面为例,分别对上表面(图中0°~180°)和下表面(图中-180°~0°)的压力系数在坐标系y轴方向分量求和,结果如表2所示。
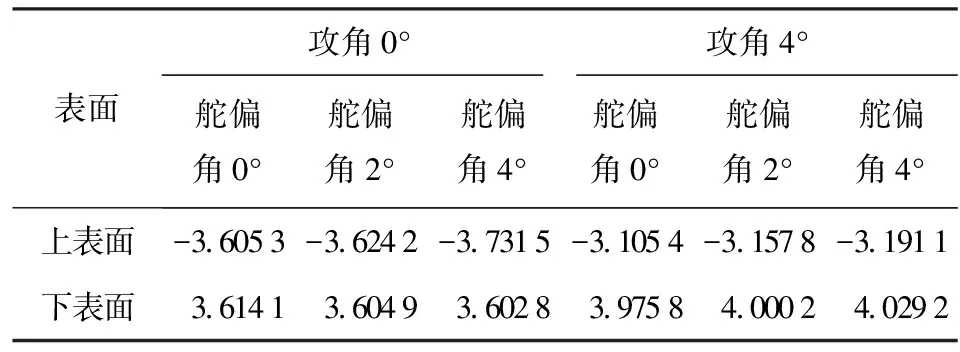
表2 y轴方向压力系数求和结果
对比以上数据可知,攻角变化对弹体y轴方向压力系数之和的影响远大于舵偏的影响。因此从图21中可以看到3种模型弹体法向力系数随攻角变化曲线高度重合。
2.3.2.2 侧向力系数
弹体受到侧向力Fz的方向为坐标系z轴方向,侧向力系数计算公式如(2)式所示。
(2)
以马赫数为0.8时3种模型的计算结果为例,绘制-8°~8°攻角下弹体侧向力系数的变化曲线,如图22所示。
从图22中可见,当马赫数为0.8时,0°舵偏模型的侧向力系数在0附近,2°舵偏和4°舵偏双旋弹道修正弹模型的侧向力系数随攻角近似线性变化。4°舵偏双旋弹道修正弹模型对应曲线的斜率大于2°舵偏模型。由此可见,非对称模型的弹体侧向力系数非对称性与鸭舵非对称布局有关,且舵偏角越大,这种非对称效应越明显。
图23给出了不同马赫数下非对称模型弹体侧向力系数随攻角的变化规律,图24给出了不同攻角下非对称模型弹体侧向力系数随马赫数的变化规律。从图23中可以观察到:不同马赫数下弹体侧向力随攻角近似线性变化。从图24中可以观察到,不同攻角下弹体侧向力随马赫数呈非线性变化;在马赫数为1.0~1.5条件下弹体侧向力系数迅速增大,并在马赫数为1.5附近达到最大值;在马赫数大于1.5时弹体侧向力系数逐渐减小;弹体侧向力系数变化幅度与攻角有关,大攻角时变化幅度大,小攻角时变化幅度较小。对比图24(a)与图24(b)可见,当攻角相同时,4°舵偏模型对应曲线峰值约为2°舵偏模型的2倍。
3 结论
为研究非对称鸭舵对弹体的影响,本文通过对比风洞实验与CFD计算的结果,验证了CFD方法的有效性。对0°舵偏、2°舵偏、4°舵偏模型在不同马赫数、不同攻角情况下进行了CFD计算,通过对结果中的弹体法向力、侧向力系数进行辨识、对比确定了非对称鸭舵对弹体的影响。所得主要结论如下:
1) 给定马赫数和攻角下,对称模型(0°舵偏模型)的弹体截面压力系数对称,非对称模型(2°舵偏模型、4°舵偏模型)弹体截面压力系数非对称。弹体表面受到鸭舵尾涡影响的区域压力系数小于相邻未受影响的区域。
2) 给定马赫数下,3种模型弹体法向力系数随攻角近似线性变化,且重合程度较高。3种模型中弹体法向力受攻角影响远大于受舵偏角影响,在工程近似计算中可以不考虑法向力系数受非对称鸭舵尾涡影响。
3) 3种模型中对称模型(0°舵偏模型)的弹体侧向力系数均在0附近。给定马赫数下,非对称模型(2°舵偏模型、4°舵偏模型)弹体侧向力随攻角近似线性变化且4°舵偏模型对应的曲线斜率更大。给定攻角下,非对称模型弹体侧向力随马赫数呈非线性变化:亚音速下变化较小,马赫数为1.0~1.5下迅速增大,并在马赫数为1.5附近达到最大值,大于马赫数为1.5时逐渐减小;大攻角时变化幅度大,小攻角时变化幅度较小。4°舵偏模型对应曲线峰值约为2°舵偏模型的2倍。
上述结论对非对称鸭舵诱导弹体产生的非对称载荷规律有了初步认识,为后续非对称鸭舵双旋弹道修正弹的气动模型修正奠定了基础。
