无线电近炸引信混沌码调相与线性调频复合调制波形设计与分析
2018-11-29陈齐乐晏祺郝新红杜涵宇
陈齐乐, 晏祺, 郝新红, 杜涵宇
(1.北京理工大学 机电动态控制重点实验室, 北京 100081; 2.中国电子科技集团有限公司 光电研究院, 天津 300308)
0 引言
电子技术的发展以及各国对电子战的日益重视,使得现代战场电磁环境日益复杂,以数字射频存储技术(DRFM)为显著特征的有源欺骗式干扰设备和装备对无线电引信构成了严重威胁。为提高引信的战场生存力,国内外开展了大量研究,并提出了各种抗干扰方法[1-3]。其中,脉冲多样性发射信号波形设计是一种有效提高引信抗干扰性能的设计方法[4]。
混沌是确定性非线性动力学系统中的随机现象,它具有随机性、初值敏感性、存在奇异引子等特殊性质,广泛应用于保密通信和雷达波形设计等领域[5]。由于混沌码类噪声特性,其非常适用于无线电引信发射信号波形脉冲多样性设计[6]。文献[7]分析了基于一维混沌序列的雷达调频、调相和调幅信号探测性能及抗干扰性能。文献[8]将基于洛伦兹映射产生的混沌序列应用于雷达波形设计,并通过调节映射参数来改善所产生的混沌序列性能。文献[9]提出利用混沌序列类正交特性,设计了多输入多输出(MIMO)雷达信号。文献[10]通过模糊函数定量分析了混沌码调相信号的分辨性能。在实际应用中,常采用数字电路生成混沌序列,并将混沌序列二值量化得到混沌码,利用混沌码调制载波相位生成发射信号。混沌码调相信号具有类图钉形模糊函数,但其频谱带宽有限,且存在编码被破解的风险[10]。调相与调频复合调制信号能够扩展带宽、提高信号抗截获性能,在保留调相信号良好相关特性的同时,还具有调频信号的宽带特性,使频谱更加复杂[11]。因此,复合调制信号距离分辨力、多普勒容限、抗干扰性能以及抗截获性能均优于单一调相信号,更加适应现代战场复杂的电磁环境。
本文根据脉冲多样性抗有源欺骗式干扰原理[12],提出一种连续波混沌码调相与线性调频复合调制信号波形。对每个线性调频周期采用不同混沌码调相,实现抗有源欺骗式干扰和复制转发类干扰,该复合调制信号频带更宽,具有更好的距离分辨力、抗截获性能和抗干扰性能。推导了复合调制信号的自相关和互相关模糊函数,定量分析了其距离分辨力、速度分辨力和影响因素,利用峰值自相关旁瓣比(PASR)和峰值互相关比(PCRR)参数衡量波形抗干扰能力,并通过MATLAB仿真软件验证了分析结论。理论与仿真结果表明,混沌码调相与线性调频复合调制波形具有更大的带宽、更好的分辨特性和更强的抗干扰性能。
1 复合调制信号
1.1 复合调制信号数学模型
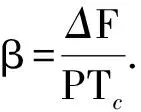
将混沌码表示为{ck,l},ck,l取值为+1或-1,其中k为1个调频周期内混沌码序号,l为调频周期序号,k=0,1,…,P-1,l=0,1,…,∞. 则ucw(t)可表示为
(1)
式中:v(·)表示时宽为Tc的门函数。
令u(t)表示ucw(t)的1个调频周期对应的波形,经能量归一化处理后u(t)可表示为
(2)
1.2 复合调制信号频域分析
根据(2)式,若取P=63,码元宽度Tc=50 ns,调制频偏ΔF=±15 MHz,则混沌码序列和复合调制波形包络信号如图1所示。
对(2)式进行分解,可得
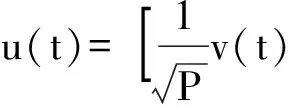
(3)
式中:δ(·)表示单位冲击响应。
根据卷积定理,复合调制信号频谱F{u(t)}可表示为
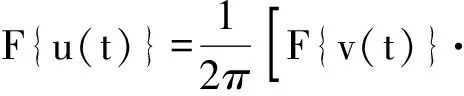
(4)
式中:
(5)
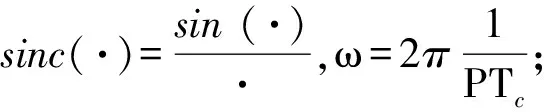
(6)
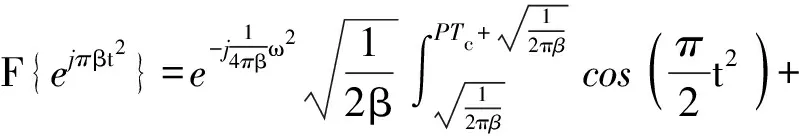
(7)
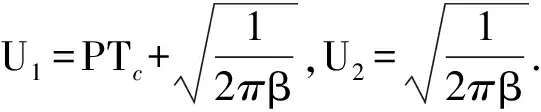
根据(4)式,复合调制信号频谱是混沌码调相信号与调频信号频谱的卷积。混沌码调相和复合调制信号频谱如图2所示。图2中码长P=31,码元宽度Tc=50 ns,调制频偏ΔF=±15 MHz.
混沌码调相信号频谱具有类辛格函数包络,其带宽为1/Tc,根据其频谱很容易估计出码元宽度Tc. 复合调制信号频谱受到线性调频的影响而具有近似矩形包络,其频谱是混沌码调相信号和线性调频信号频谱的卷积,频带更宽,因此探测性能、抗干扰性能和抗截获性能更强。由于频带受码元宽度Tc和调制频偏ΔF的共同作用,很难通过频谱分析来估计调制参数。
1.3 模糊函数推导
根据文献[12]介绍的模糊函数两种形式,复合调制信号自相关模糊函数以及互相关模糊函数表达式可分别写为(8)式和(9)式:
(8)
(9)
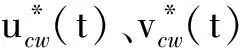
单纯混沌码调相信号可以表示为

(10)
根据模糊函数性质[13],若χpma(τ,fd)表示混沌码调相信号模糊函数,则
(11)
式中:
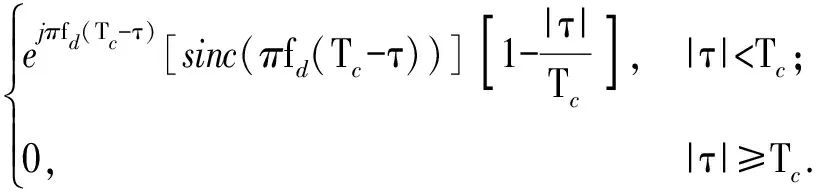
(12)
经计算可得到uc(t)的模糊函数如下:
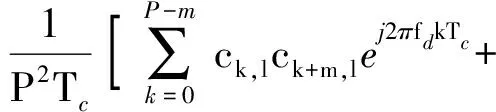
(13)
式中:τ=mTc,m=0,1,2,…,P.
又由模糊函数性质[14]
χhma(τ,fd)=e-jπβτ2χpma(τ,fd-βτ).
(14)
综合(10)式、(11)式、(13)式和(14)式,可得复合调制信号自相关模糊函数为

(15)
式中:|τ-mTc| 同样地,可求得复合调制信号互相关模糊函数为 (16) 式中:l′=0,1,…,∞,l′≠l. 1个调频周期长度的混沌码调相信号及复合调制信号自相关模糊图如图3(a)和图3(b)所示,不同调频周期对应的两段复合调制发射信号互相关模糊函数如图3(c)所示。其中码长P=63,码元宽度Tc=50 ns,调制频偏ΔF=±15 MHz. 从图3中可以看出,复合调制波形保留了混沌码良好的相关特性。自相关模糊函数具有类图钉型的尖锐相关峰,互相关模糊函数值在整个模糊面均很低,复合调制信号模糊图是混沌码调相信号模糊图的剪切旋转。尖锐的自相关峰决定复合调制信号具有优秀的分辨特性,低自相关旁瓣及互相关函数决定复合调制信号具有极强的抗有源欺骗式干扰性能。 根据自相关模糊函数的物理意义,当fd=0 MHz时,χhma(τ,0)即为距离自相关函数。将fd=0 MHz分别代入(12)式、(15)式,混沌码调相信号及复合调制信号距离自相关函数为 (17) 复合调制信号距离模糊函数为 (18) 分析(17)式和(18)式可知,两种信号的距离自相关函数主要由混沌码自相关性能决定,且复合调制信号的距离自相关函数还受到调频影响,因此其主瓣更尖锐、旁瓣更低。混沌码调相信号和复合调制信号的距离模糊图如图4所示。对比图4(a)和图4(b)可以看出,复合调制信号距离模糊图主瓣更尖锐、旁瓣更低。 以距离自相关函数主瓣6 dB宽度定义为信号固有分辨力,并称之为名义分辨力[13]。定义τs为名义分辨力,则根据定义可知: χ(τs,0)=0.5. (19) 将(17)式代入(19)式,经分析模糊函数主瓣对应m=0,解得混沌码调相信号名义分辨力(主瓣6 dB宽度): τs1=0.5Tc. (20) 当m=0时,化简(18)式得 (21) (22) 图5所示为在不同调制频偏或码元宽度条件下名义分辨力的变化。由图5可以看出:单一混沌码调相信号名义分辨力取决于码元宽度,而复合调制信号距离分辨力受码元宽度和调制频偏共同作用;当ΔF≥1/Tc时,复合调制信号名义分辨力取决于调制频偏;当ΔF<1/Tc时,名义分辨力取决于码元宽度。 根据自相关模糊函数的物理意义,取τ=0 μs,即可得速度模糊函数。将τ=0 μs代入(12)式和(15)式,可得到单一混沌码调相信号和复合调制信号速度模糊函数完全一致,其结果为(23)式: (23) (24) 图6所示为在不同码元宽度或码长条件下多普勒分辨力的变化情况。由图6可知,速度分辨力随着码元宽度或码长增加而提高,与理论分析一致。 综上所述:复合调制信号距离分辨力在ΔF≥1/Tc条件下,取决于调制频偏;在ΔF<1/Tc条件下,取决于码元宽度。速度分辨力随着码元宽度或每个调频周期内码元个数的增加而提高,仿真结果验证了该结论。 信号自相关旁瓣会掩盖微弱小目标回波、造成漏警,或者形成虚假目标、造成虚警。根据脉冲多样性抗干扰原理,若要信号具有很强抗复制转发式干扰能力,则不同时段发射信号要具有类正交特性。因此发射信号波形相关性能直接影响探测器探测性能及抗干扰性能。 根据峰值自相关旁瓣比(PASR)定义[14],复合调制信号峰值自相关旁瓣比ΔPASR可表示为 ΔPASR=sup [|χhma(τ,0)|2/|χhma(0,0)|2]= sup[|χhma(τ,0)|2],τ>Tc, (25) 即峰值自相关旁瓣比取决于旁瓣最大值, (26) 又知当τ>Tc时, max{sinc[-πβτ(Tc-|τ-mTc|)]}≤1, 以及 可得 (27) 即复合调制主旁瓣比小于混沌码自相关最大旁瓣。根据数值分析,当P=63时,归一化后混沌码自相关旁瓣值约为0.25,因此复合调制信号主旁瓣比ΔPASR<0.25. 根据复合调制信号距离自相关仿真图(见图4(b))可以得出ΔPASR≈0.2. 根据峰值互相关比(PCRR)定义[14],任意不同两段调频周期对应的复合调制信号ΔPCRR为 ΔPCRR=sup [|χhmc(τ,0)|2/|χhma(0,0)|2]= sup[|χhmc(τ,0)|2], (28) 即复合调制信号ΔPCRR取决于信号互相关函数最大值。 将fd=0 MHz代入(17)式,根据复合调制信号距离互相关函数 |χhmc(τ,0)|= 可得 (29) 即复合调制信号PCRR小于混沌码互相关函数最大值。根据数值分析,当P=63时,混沌码互相关函数最大值约为0.25,因此ΔPCRR<0.25. 复合调制信号互相关函数仿真结果如图7所示(仿真参数同互相关模糊图)。从图7可知,复合调制信号互相关最大值约为0.2,与理论一致,因此不同调频周期对应的两段复合调制信号具有类正交特性。 综上所述可知,复合调制信号具有良好的相关特性,其在降低虚警和漏警概率、抗有源欺骗式干扰等方面性能优异,具有更强的抗干扰性能。 下面将本文提出的复合调制波形应用于文献[15]设计的复合调制体制引信中,通过仿真分析其输出检波信号,来验证该波形的距离分辨特性以及抗干扰性能。复合调制引信原理框图如图8所示。 仿真参数设置如下:线性调频调制周期T=PTc,P=63,码元宽度Tc=50 ns,调制频偏ΔF=±15 MHz,引信载波f0=3 GHz,弹目相对运动速度v=1 000 m/s. 目标回波作用下引信包络检波输出信号如图9所示,图中U为引信输出电压,H为弹目距离。 给引信施加功率与发射信号功率相同的DRFM干扰时,引信检波输出如图10所示,其中DRFM延时为范围0~0.001的随机数。从图10中可以看出,当受到DRFM干扰时,由于引信发射波形不同调频周期的两段信号类正交特性,系统输出检波信号能量很小,系统具有极强的抗DRFM干扰能力。 在微波暗室测试混沌码调相与线性调频复合调制引信测距及抗有源欺骗式干扰性能,复合调制引信频偏ΔF=±15 MHz,其他参数同前述。原理样机测距性能交会场景如图11所示,面积为1 m2金属平板放置在距离引信样机脱靶量6 m位置,以1 m/s速度与样机相向交会,引信系统经二次混频后输出的多普勒信号um(t)如图12所示。由图12可知,引信在目标回波作用下可实现定距功能。 3种干扰作用下,引信系统经二次混频后输出的多普勒信号um(t)如图13所示。其中,干扰场景设置为引信样机距离干扰试验系统6 m,干扰试验系统与引信样机天线主瓣互相对准,干扰功率稍大于相同距离处目标回波在引信接收端的功率密度,3种窄带瞄准式干扰信号的载波对准引信频率f0. 其中噪声调幅干扰参数:加载高斯白噪声,调幅深度100%;噪声调频干扰参数:加载高斯白噪声,调制频偏15 MHz;锯齿波线性调频干扰参数:调制频偏15 MHz,锯齿波调制频率10 kHz. 由测试结果可知:噪声调频、噪声调幅干扰作用下复合调制引信多普勒检波端无包络峰值输出;线性调频干扰作用下,引信检波输出有不规则虚假峰值出现,该类干扰信号可在后期多普勒信号处理中引入目标回波信号的时序逻辑和增幅速率特征加以识别。因此,复合调制引信具有抗噪声调幅、噪声调频和线性调频干扰能力。 本文以自相关模糊函数及互相关模糊函数为工具,对混沌码调相与线性调频复合调制信号的探测性能及抗干扰性能进行了定量分析。所得主要结论如下: 1)复合调制信号具有类图钉型模糊函数,旁瓣很低,具有很好的分辨性能及抗干扰性能。 2)距离分辨力受到码元宽度和调制频偏共同作用,随着码元宽度的减小、频偏的增大而提高。 3)速度分辨力反比于码长和码元宽度的乘积。 4)复合调制信号在不同调频周期内采用不同混沌码调制,两段不同周期的复合调制信号保留了混沌码类正交特性,具有更强抗有源欺骗式干扰性能。 5)复合调制信号波形更能满足现在战场复杂电磁环境下的作战要求,具有良好的应用前景。
2 分析和讨论
2.1 距离分辨力


2.2 速度分辨力

2.3 抗干扰性能分析
2.4 复合调制引信仿真结果分析
3 样机实验验证
4 结论
