无人机编队保持反步容错控制

2018-11-29李炳乾董文瀚马小山

兵工学报 2018年11期

李炳乾，董文瀚，马小山

(1.空军工程大学研究生院，陕西西安 710038； 2.空军工程大学航空工程学院，陕西西安 710038)

0 引言

随着无人机(UAV)技术的迅速发展，UAV编队在目标搜索、抢险救灾及执行军事任务方面将发挥越来越重要的作用，UAV编队控制已成为学者们研究的热点问题[1]。目前常用的编队控制方法主要有以下3种：一是领导-跟随法[2]，即通过对长机速度、航迹方位角和航迹倾斜角的跟踪来调整僚机，达到保持编队队形的目的；二是虚拟结构法[3]，即通过跟踪虚拟结构的状态信息进行编队控制，以实现精确的编队队形保持，但是编队信息交互较为复杂；三是分布式控制[4]，即每架UAV与编队中相邻的UAV进行信息交互，以实现编队控制。另一方面，UAV编队飞行过程中，可能会发生执行器、传感器和结构的失效、损伤等导致的故障[5]，此时飞行控制系统如果能够及时地检测和辨识系统故障并采取一定的容错控制，使得飞机继续完成任务或安全返航，则将极大地提高UAV的生存性。因此研究UAV编队的容错控制问题具有重大军事意义。

近几年来，国内外学者越来越关注UAV编队容错控制的研究，并取得了一定进展。文献[6]首先针对UAV编队中的领导者设计滑模控制方法，使得领导者可以准确跟踪编队指令信号，然后针对跟随者设计基于模型预测的容错控制，并对所提的编队容错控制方法进行了数字仿真和实验验证，结果表明所设计的方法可以实现包容执行器故障的编队容错控制；文献[7]首先根据UAV编队中领导者和跟随者的横向误差和纵向误差，建立了二维编队运动模型，并对其进行外环编队控制，产生跟随者的编队跟踪指令，然后设计模型参考自适应容错控制并进行稳定性分析，通过数字仿真验证了所设计方法能够有效实现编队容错控制；文献[8]针对UAV编队中的领导-跟随编队拓扑结构，提出一种故障估计算法，并在该算法基础上设计了自适应容错控制，实现了包容参数不确定性和执行器故障的容错控制，并对编队容错控制的暂态性能进行了改善；文献[9]首先通过设计干扰观测器来估计UAV编队飞行过程中发生的执行器故障、传感器故障和所受的外界扰动，然后分别针对UAV的速度回路和姿态回路设计容错控制器，其中在姿态回路控制律设计过程中，将观测器与反步法相结合，实现UAV编队容错控制，最后进行了系统稳定性分析，并通过数字仿真证明了所提方法对UAV编队容错控制的有效性；文献[10]针对UAV领导-跟随编队拓扑结构，提出了一种基于模型预测控制的路径规划算法以及包容执行器故障和传感器故障的容错控制方法，并通过数字仿真证明了所提方法对编队容错控制的有效性；文献[11]针对固定翼飞机紧密编队设计了一种多模型自适应故障辨识和容错控制方法，以保证编队系统的稳定性和编队误差的有界性，并通过数字仿真验证了所提方法的有效性；文献[12]设计了干扰观测器用于对紧密UAV编队涡流和执行器故障进行估计，分别提出纵向反步控制律和横向反步控制律，实现了包容涡流和执行器故障的紧密编队反步容错控制；文献[13]针对UAV编队中的领导-跟随编队拓扑结构，提出一种基于模型预测控制的路径规划算法以及包容执行器故障和传感器故障的容错控制方法，并通过数字仿真证明了该方法可以有效地包容执行器和传感器故障，实现UAV编队保持的容错控制。

本文针对UAV编队中的领导-跟随编队拓扑结构，提出一种反步容错控制方法。首先对三维编队方程、UAV非线性方程和执行器故障模型进行分析，然后针对三维编队模型设计编队外环控制器来产生编队指令信号，最后设计内环容错控制系统来对编队指令信号进行跟踪，实现编队稳定控制。内环容错控制系统主要包括3个部分：一是故障检测与辨识机制，用来定位故障执行器并估计故障参数；二是将故障参数及干扰观测器与反步容错控制结合，实现包容外界扰动、不确定气动参数及执行器故障的容错控制；三是内环容错控制系统稳定性分析。

本文的创新点主要有：1)针对编队飞行中的执行器故障、外界扰动及不确定参数，将反步控制与故障辨识参数估计、自适应观测器和参数自适应律相结合，实现包容执行器故障、外界扰动和不确定气动参数的编队保持容错控制；2)对执行器故障进行建模，并针对故障模型设计故障辨识器，实现对故障类型的精确辨识和故障参数的估计；3)设计自适应干扰观测器，对外界扰动、建模误差等不确定性进行补偿，实现包容外界扰动的鲁棒控制；4)设计不连续投影自适应律来对不确定气动参数进行补偿，实现对参数不确定性的鲁棒控制。

1 问题描述

本文所采用的UAV编队拓扑结构为领导-跟随结构，下面主要对编队运动模型、UAV非线性模型和执行器故障模型进行描述。

1.1 编队运动模型

领导者UAVL和跟随者UAVi的三维编队运动模型分别为

(1)

(2)

式中：xL、yL、zL分别为UAVL质心位置在地理坐标系中的投影坐标；vL、ψL、θL分别为UAVL速度、航向角和俯仰角；xi、yi、zi分别为UAVi质心位置在地理坐标系中的投影坐标；vi、ψi、θi分别为UAVi速度、航向角和俯仰角。

如图1所示，UAVi与UAVL的纵向误差、横向误差和高度误差可以表示为

(3)

对(3)式求导，进一步可以得到编队外环误差模型为

(4)

1.2 UAV运动模型

UAV非线性模型可由12个1阶微分方程描述[16]。根据时标分离法，将飞机本体方程分为快回路和慢回路进行分析。快回路由ω=[pqr]T3个状态量组成，其中p、q、r分别为滚转角速度、俯仰角速度和偏航角速度；慢回路由Ω=[ψθβ]T3个状态量组成，其中ψ、θ、β分别为航向角、俯仰角和侧滑角。慢回路和快回路方程可以描述为

(5)

式中：fs(Ω)和Gs(Ω)分别为慢回路方程中的非线性部分和操纵力矩矩阵；ff(ω)和Gf(ω)分别为快回路方程中的非线性部分和操纵力矩矩阵；u=[δaδeδrδp]T为飞机实际的控制指令，其中δa、δe、δr、δp分别为副翼、升降舵、方向舵和油门杆的偏转角度。

当飞行器进行机动动作时，其气动非线性、不对称性、交叉耦合和迟滞特性使得气动参数具有不确定性；当飞机受到外界扰动影响时，会产生一个不确定性d. 则包含不确定参数和不确定性d的慢回路和快回路方程(5)式可以描述为

(6)

式中：Fs(Ω)、A(Ω)和θΩ∈R3分别为慢回路方程的非线性部分、不确定参数系数矩阵和不确定气动力参数；Ff(ω)、B(ω)和θω∈R12分别为快回路方程的非线性部分、不确定参数系数矩阵和不确定气动力矩参数。

1.3 执行器故障模型

执行器作为控制指令信号到舵面的传递装置，其动态方程[17]可以描述为

(7)

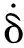
当执行器发生故障时，实际表现为舵面发生异常偏转。在实际飞行控制系统中，典型的执行器故障可以分为卡死、饱和、松浮和损伤4类。其中，饱和故障等效为舵面卡死在极限位置处，松浮故障等效为舵面卡死在0°位置处，二者均可视为卡死故障的特殊情况，因此将饱和故障和松浮故障统一视为卡死故障进行分析。卡死故障的动态方程可以描述为

(8)

式中：δ(tf)为发生卡死故障时的舵面偏角，tf为故障发生的时间；t为执行器工作时间。

损伤故障的动态方程可以描述为

(9)

式中：k∈(0,1]为损伤故障系数，k=1表示执行器无损伤故障，k∈(0,1)表示执行器发生不同程度的损伤故障。则执行器故障模型[15]可以描述为

(10)

式中：σ∈{0,1}为卡死故障系数，σ=0表示执行器发生卡死故障，σ=1表示执行器无卡死故障。由于a≫0，由奇异摄动理论可以将故障模型(10)式化简为

δ=σkδc+(1-σ)δ(tf).

(11)

δ=σkδc+(1-σ)δ,

(12)

进而可以得到

u=ΣKuc+(I-Σ)u,

(13)

式中：Σ=diag[σa,σe,σr,σp]，σa、σe、σr、σp分别为副翼执行器、升降舵执行器、方向舵执行器和油门杆执行器的卡死故障系数；K=diag[ka,ke,kr,kp]，ka、ke、kr、kp分别为副翼执行器、升降舵执行器、方向舵执行器和油门杆执行器的损伤故障系数；uc=[δcaδceδcrδcp]T，δca、δce、δcr、δcp分别为副翼执行器、升降舵执行器、方向舵执行器和油门杆执行器的输入指令信号；I为单位矩阵向量。则包含不确定气动参数、不确定性及执行器故障的UAV模型可以描述为

(14)

2 编队外环控制器设计

将编队模型(4)式变形为

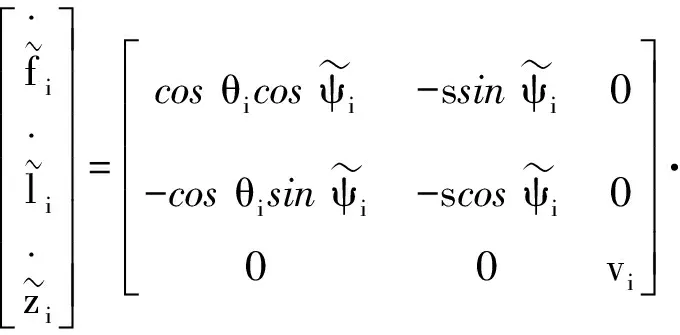
(15)

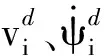
(16)

式中：k1、k2、k3为反馈增益，且k1>0，k2>0，k3>0.

将(16)式代入(15)式并化简得

(17)

进一步可以得到编队内环速度、航向角和俯仰角指令信号为

(18)

式中：ψi(0)为初始航向角。

3 编队内环容错控制系统设计

下面设计UAV编队内环控制系统，对编队外环指令进行跟踪。本文所提容错控制方法主要有以下特点：一是可以与UAV领导-跟随编队控制结合，实现包容不确定气动参数、外界干扰和执行器故障的编队容错控制；二是可以对所有UAV的所有具体执行器进行故障辨识和估计，并对执行器故障进行自适应补偿；三是分别针对外界扰动和不确定气动参数设计自适应干扰观测器和不连续投影自适应律，实现编队的鲁棒控制。本文的设计内容对编队内所有无人飞行器均适用，为了便于分析，不对领航者和跟随者区分说明。

3.1 故障检测和辨识

3.1.1 不连续投影算子

为了对执行器故障进行检测和辨识，下面对不连续投影算子进行介绍并给出定义。

定义：θ∈Rp为未知参数向量，其中Rp表示p维向量；为θ的估计值，-θ为θ的估计误差，则为的不连续投影自适应律，其中Ψ>0为对角矩阵，ε为任意自适应函数，Proj(·)为不连续投影算子：

Proj(·)=[Proj(·1),…,Proj(·p)]T,

不连续投影自适应律具有如下性质：

性质1i∈[θimin,θimax],i=1,…,p.

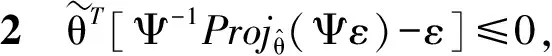
证明由不连续投影算子的定义可知性质1成立，即i∈[θimin,θimax],i=1,…,p.

其他情况下，Proj(Ψε)i=(Ψε)i，则Ψ-1Proj(Ψε)-ε=0. 可以得到对于∀ε成立。

综上所述，不连续投影自适应律的性质2成立。

3.1.2 故障检测与辨识设计

针对每个舵面分别设计卡死故障滑模观测器和损伤故障滑模观测器，实现故障类型辨识和故障参数估计。

卡死故障滑模观测器设计如下：

(19)

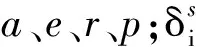
损伤故障滑模观测器设计如下：

(20)

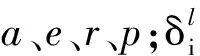
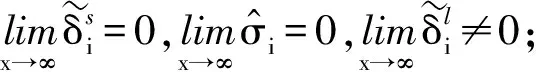
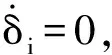
构造Lypunov函数如下：

则

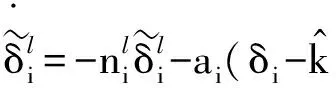
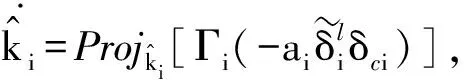
当第i个执行器发生损伤故障时，卡死故障滑模观测器误差微分方程为

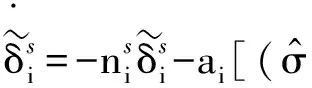
当第i个执行器发生损伤故障时，损伤故障滑模观测器误差微分方程为

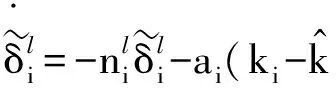
构造Lypunov函数如下：

则

根据结论1设定以下指标，对卡死故障和损伤故障进行辨识：

(21)

(22)

(23)

由结论1可以进一步得到以下推论：

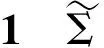
证明当观测器观测到执行器发生卡死故障时，由结论2可得i=0、i=1，而实际上发生卡死故障时有σi=0、ki=1，从而可以得到同理，当发生损伤故障时，有进而可知和收敛。

3.2 容错控制器设计

3.2.1 慢回路控制器设计

定义姿态角误差为

Ωe=Ω-Ωc,

(24)

式中：Ωc=[ψcθcβc]T为编队内环控制指令信号。则对(24)式求导并将(6)式代入(24)式，可得

(25)

则由(25)式可设计慢回路虚拟指令信号为

(26)

式中：KΩ为正定矩阵；Ω为θΩ的估计值，的自适应律设计如下：

(27)

式中：ΓΩ和λΩ为正定矩阵。将虚拟控制信号(26)式和自适应律(27)式代入(25)式，可得

(28)

3.2.2 快回路控制器设计

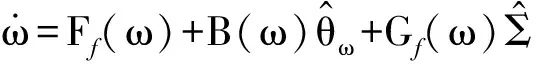
(29)

(30)

式中：Γω和λω为正定矩阵。定义角速度误差为

ωe=ω-ωc,

(31)

式中：ωc为快回路虚拟控制信号。则

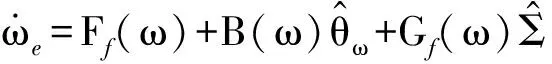
(32)

最终控制信号设计为

uc=-[Gf(ω)]-1[Kωωe+B(ω)θω+Ff(ω)+
Gf(ω)(I-)u+

(33)

将(33)式代入(32)式，可得

(34)

3.2.3 自适应干扰观测器设计

下面针对快回路误差方程(32)式设计自适应干扰观测器，对不确定性d进行估计。自适应干扰观测器设计如下：

(35)

结论2若ω的自适应律(30)式收敛，则高阶干扰观测器(35)式也收敛。

证明从文献[18]可得以下引理：

进而可以得到

3.3 系统稳定性分析

飞行器作机动动作时，其本体参数、气动参数和各姿态角是不断变化的，但是实际飞行中它们都有一定的界限。基于此提出两个假设：

假设1存在一个正常数ρ1，使得对于任何Ω∈UΩ，都有‖Gs(Ω)‖≤ρ1.

假设2存在一个正常数ρ2，使得对于任何ω∈Uω，都有‖B(ω)‖≤ρ2.

结论3考虑系统(14)式，设计控制律为(33)式，自适应律为(27)式和(30)式，自适应干扰观测器为 (35)式，则此系统渐近稳定，即编队内环可以稳定跟踪外环指令信号(18)式，最终实现编队稳定控制。

证明构造Lypunov函数如下：

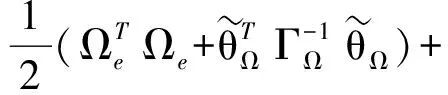
则

将自适应律(27)式和(30)式代入上式，且由不连续投影自适应律性质2，可得

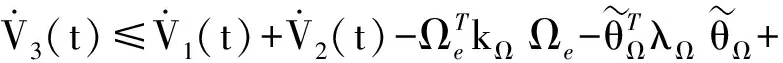
由完全平方不等式可得

(36)

式中：kΩ min、kωmin、λΩ min、λωmin和Limin(ωe)分别为KΩ、Kω、λΩ、λω和Li(ωe)矩阵的最小元素。

(37)式即为控制器稳定的参数设定条件：

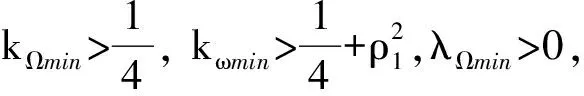
(37)

以上是无人机编队保持反步容错控制系统设计

4 仿真结果与分析

4.1 仿真1：简单故障情况下的编队仿真

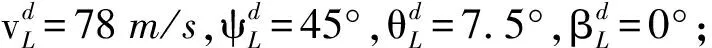
整个仿真时间为100 s，选取参数不确定性为Δθω∈[(1-30%)θω,(1+30%)θω],ΔθΩ∈[(1-20%)θΩ,(1+20%)θΩ]，选取外界扰动d=[dpdqdr]T，其中dp=dq=dr=10sin (2πt)°/s2. 整个仿真过程中，设定以下故障：UAV1在t=30 s时方向舵执行器发生损伤系数为60%的损伤故障，UAV2在t=60 s时升降舵执行器发生卡死故障。基于(37)式控制器设计要求，并经过多次调试，选取控制器主要参数如表1所示。

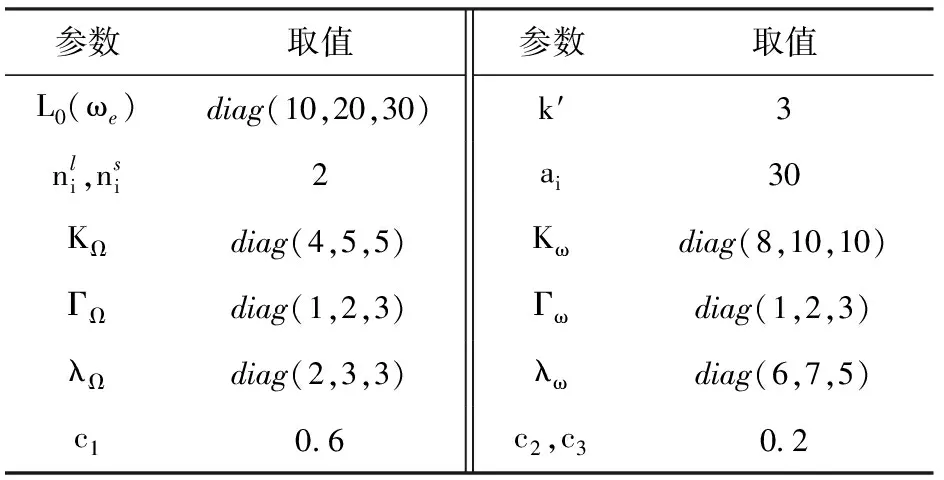
表1 控制器参数

为了验证本文所设计控制器的容错性能，在外界扰动d、不确定气动参数和执行器故障的影响下，首先采用本文所设计的容错控制器进行仿真，然后采用不包括自适应干扰观测器(35)式、参数自适应律(27)式、(30)式及故障参数、的一般控制器进行仿真。两种控制器的对比仿真曲线如图3～图7所示。

图3为容错控制器与一般控制器的三维编队轨迹对比仿真图。由图3可以看出：当t<30 s时，即执行器故障发生之前，容错控制器可以实现补偿外界扰动和不确定气动参数的鲁棒控制，而一般控制器的三维轨迹发生波动，不能有效补偿外界扰动和不确定气动参数影响；当t=30 s时，UAV1的方向舵执行器发生损伤系数为60%的损伤故障，其中容错控制器在发生微小波动之后继续保持编队运动，而一般控制器则发生大幅度不规则波动，不能继续保持编队运动；当t=60 s时，UAV2的升降舵执行器发生卡死故障，容错控制器和一般控制器的仿真图分析情况与UAV1方向舵执行器故障类似。

图4和图6分别为UAV1和UAV2的纵向距离、横向距离和高度距离对比仿真曲线，可见容错控制器与一般控制器的对比分析结果与图3类似。图5和图7分别为UAV1和UAV2的速度、航迹方位角和航迹倾斜角对比仿真曲线，可见容错控制器能够实现包容外界扰动、不确定气动参数及执行器故障的容错控制，实现对编队控制指令的跟踪；而一般控制器既不能实现对外界扰动和不确定气动参数的鲁棒控制，也不能实现对执行器故障的容错控制。

图8为故障参数辨识仿真曲线。由图8可以看出，UAV1在t=30 s时方向舵执行器发生损伤系数为60%的损伤故障，UAV2在t=60 s时升降舵执行器发生卡死故障。故障辨识结果与故障设置相同，进一步验证了本文所设计故障辨识器的准确性和有效性。

4.2 仿真2：复杂故障情况下的编队仿真

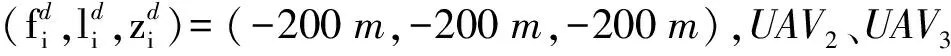
编队仿真时间为100 s，控制器参数设置如表2所示，其余编队指令与仿真1中相同。执行器故障情况如表2所示。

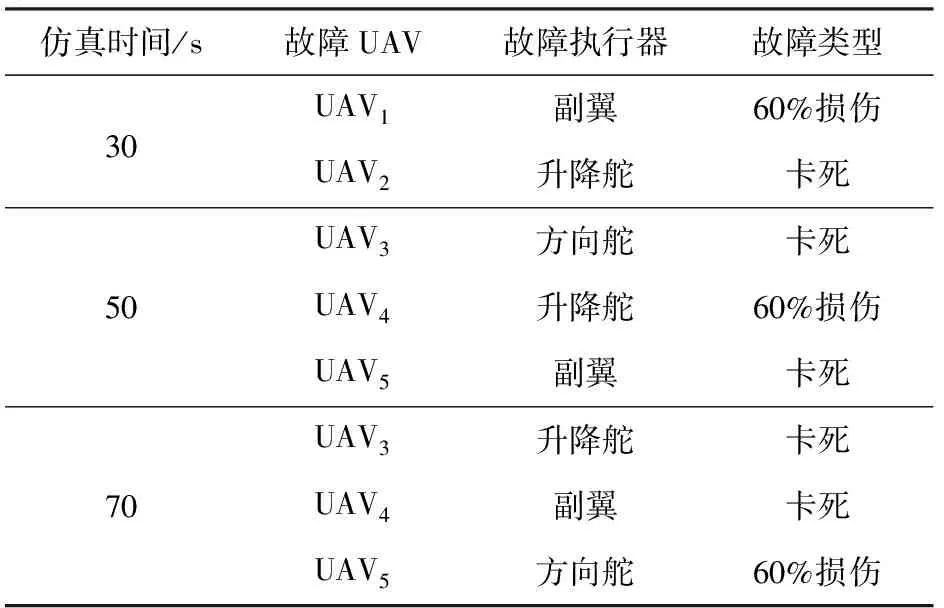
表2 仿真中执行器故障

与仿真1类似，本节仍然对容错控制器和一般控制器进行对比仿真，仿真结果如图10所示。仿真结果分析过程与图3类似，通过仿真分析可知本文所设计编队容错控制方法在复杂故障条件下仍然可以实现包容外界扰动、不确定气动参数和执行器故障的容错控制，最终实现编队稳定飞行。

本仿真算例中各UAV的指令跟踪仿真结果与仿真1中指令跟踪结果类似，限于篇幅，不再赘述。

4.3 仿真3：领导者故障情况下的编队仿真

下面对编队领导者故障情况下的编队飞行进行仿真。设定编队领导者在t=10 s时升降舵执行器发生卡死故障，t=20 s时方向舵执行器发生60%损伤故障。其余仿真条件及故障设定与仿真2完全相同。仿真结果如图11所示。由图11可见，当领导者发生执行器故障时，在容错控制器作用下，领导者和编队其他所有跟随者在发生微小波动后继续保持编队稳定飞行，而在一般控制器作用下，领导者不能补偿执行器故障，运动轨迹振动剧烈且误差过大，进而其他UAV跟随领导者振动。综上所述可知，本文所设计编队容错控制方法在领导者故障条件下仍然可以实现包容外界扰动、不确定气动参数和执行器故障的容错控制，最终实现编队稳定飞行。

整个仿真过程表明，本文所设计的容错控制系统能够在简单故障、复杂故障及领导者故障情况下均能实现包容外界扰动、不确定气动参数及执行器故障的容错控制，保持编队稳定飞行。