长期车辆合乘问题的复合变邻域搜索算法

郭羽含，伊 鹏

(辽宁工程技术大学 软件学院，辽宁 葫芦岛 125100)(*通信作者电子邮箱591729781@qq.com)

0 引言

随着我国经济的高速发展，私人汽车保有量急剧增加，导致城市交通拥堵和环境污染情况日益严重。为缓解以上问题并提升市民的出行效率，顺风车、网约车等车辆合乘模式开始涌现。但传统车辆合乘均采用即时匹配模式，缺乏稳定性且每天均需重复匹配过程，用户需要频繁操作且对计算资源的耗费十分巨大。本文研究的长期车辆合乘为解决以上弊端提供了新的手段。长期车辆合乘主要针对于大中型城市中具有相同或相近的上下班时间和工作地点，但居住分散的用户群体。合乘用户在成功匹配之后，其合乘关系将长期保持无需再次匹配。这种合乘模式可在很大程度上提高用户合乘的便利性，增加参与合乘的用户数量，继而减少私人汽车出行率、降低出行花费、缓解城市交通压力和减少污染物的排放。

长期车辆合乘问题(Long-Term CarPooling Problem，LTCPP)中用户目的地相对固定且用户间合乘关系长期保持相对稳定，属于一种特殊的车辆路径规划问题(Vehicle Routing Problem,VRP)。传统的车辆路径问题研究主要针对仓储物流配送问题进行路径规划，而长期车辆合乘问题在路径规划的基础上还需构建合乘小组，因此还涵盖了分组问题，求解更为复杂且时空约束数量更多。国内外关于长期车辆合乘问题的研究起步较晚，研究数量较少，多数研究均针对传统车辆路径规划问题或单次车辆合乘问题。宋超超等[1]提出一种基于吸引粒子群算法解决车辆合乘问题，通过吸引粒子群算法进行初次匹配，然后通过匹配再优化的策略对合乘方案进行再优化，最后得到搭载成功率较高的车辆合乘匹配方案。杨志家等[2]提出一种分布式并行计算环境下的合乘模型，利用合乘概率矩阵的先验知识对车辆合乘问题实现高效的运算和求解。Boukhater等[3]提出一种改进的遗传算法以最小的旅行距离、高效的搭乘匹配、及时到达和最大的公平性来搜索解决方案。目前的研究主要针对小规模车辆合乘问题[4-6]，对于较大规模算例求解存在求解效率低、求解质量差的问题。而变邻域搜索算法是一种快速有效的算法，可以在短时间内求出车辆路径问题的近似解或最优解。

本文针对长期车辆合乘问题提出了涵盖车容量和时间窗约束的全面数学模型，并在变邻域搜索的基础上提出了一种有效的复合算法。变邻域搜索算法具有算子设计自由度高、收敛速度快、不易陷入局部最优等特点，本文针对长期车辆合乘问题特点设计了专用算子，可在短时间内求得高质量的解决方案。仿真实验结果表明该算法求解质量高，且运算时间短，具有很高的时效性。

1 问题描述

1.1 问题定义

假设每位合乘参与者都拥有各自的车辆，并前往相同的目的地。每位参与者可单独驾车或与他人合乘，且每位用户都有各自的最长行驶时间和最大搭载量。长期车辆合乘问题的目标是求出一种合乘方案，将参与者分到若干个合乘小组中，小组中的用户按固定规律轮流驾驶各自的车辆按照算法计算出的最短路径接送组内其他用户抵达目的地，使得所有小组的出行花费总和达到最低。

1.2 合乘模型

1.2.1 常量定义

在本模型中：S表示合乘的解决方案；每个合乘小组P包含该合乘小组的所有用户；C表示所有用户的集合；capcj表示当用户cj作为司机时能够搭载的最大人数；timcj表示用户cj作为司机时能够接受的最长行驶时间；arvcj表示用户cj最晚到达目的地的时间；ecj表示用户cj最早出发时间。

1.2.2 变量定义

φcj表示用户cj是否独自驾车，若该用户独自驾车则变量φcj为0，否则为1；numPk表示合乘小组Pk的实际搭载人数；QPk表示合乘小组Pk的车容量；arrtcj表示合乘小组中用户cj到达目的地的时间；TlPk表示合乘小组Pk最晚到达目的地的时间。

1.2.3 目标函数

LTCPP优化目标在于降低用户出行总花费，由于每位司机可以有多条行车路线，因此算法通过路径规划对合乘小组Pi中每位用户找到一条最短路径。costcj表示在合乘小组Pi中用户cj作为司机时用户cj的最少出行费用，为了减少单独驾车的情况出现，本文引入惩罚因子ρ(1<ρ<2)，单独驾车的用户将会受到惩罚；合乘小组Pi的人数定义为numPi总费用为cost(Pi)。

(1)

目标函数为：

(2)

其中fLTC为所有合乘小组的出行总花费。

1.2.4 约束条件

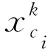
QPk=min(capcj);Pk∈S,∀cj∈Pk

(3)

(4)

1≤numPk≤QPk;Pk∈S

(5)

ecj≤TlPk-arrtcj;cj∈Pk,Pk∈S

(6)

TlPk≤min(arvci);ci∈Pk,Pk∈S

(7)

arrtcd≤timcd;cd∈P

(8)

φci∈{0,1};ci∈Pk,Pk∈S

(9)

(10)

其中：式(3)～(5)表示合乘小组载客量约束;式(4)表示司机cd经过用户ci点，将用户ci载入合乘小组Pk中后合乘小组Pk中的人数；式(6)限定了用户最早出发时间；式(7)限定了合乘小组最晚到达目的地时间；式(8)限定了合乘小组中司机的行驶时间；式(9)、(10)为二进制完整约束。

2 初始解决方案

为了得到合乘小组成员地理分布合理的初始解，本文设计两步法生成初始解：第一步进行司机的筛选；第二步应用Regret Insertion算法构造初始解；并且采用双层编码的结构显示合乘小组中各个用户的信息。双层编码结构如图1所示。第一层编码中包含合乘小组的用户编号及分组方式；第二层编码显示第一层中的用户作为司机时的详细信息，依次包括合乘小组成员、到达小组其他用户位置的时间、是否独自驾车、行驶距离、司机可接受的最长行驶时间和合乘小组到达目的地时间。

图1 双层编码结构Fig. 1 Two-levels structure

2.1 司机的筛选

1)在用户集合中随机筛选一名用户ci作为司机，构建一个合乘小组Pi。

2)在用户集合中选出距离用户ci最近的m个用户，然后将这m个用户从用户集合C中删除。

(11)

其中n为用户集合C的用户数量。

3)重复1)、2)操作直至用户集合C为空。

这样可以避免选择两个距离太近的用户c1和c2来构建两个合乘小组，从而减少由于组间用户距离过近对合乘小组造成质量上的影响。

2.2 初始解的构造

应用Regret Insertion算法，基于上一步没有被选为司机的用户的Regret值将用户分配到合乘小组中。通过式(12)计算每一位未被选择为司机的用户ca与每位司机cb之间的距离。

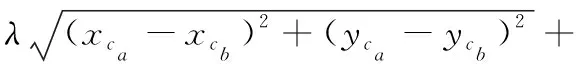
μ|eca+tcacb-ecb|

(12)

其中：xca、yca、xcb、ycb分别为用户ca和用户cb的地理坐标；eca和ecb分别为用户ca和用户cb的最早出发时间；tcacb为司机从用户ca行驶到用户cb所需要的时间；|eca+tcacb-ecb|为用户ca到用户cb可接受的时间与实际从用户ca到用户cb行驶时间的偏差；λ和μ为影响因子。然后计算用户ca的Regret值，如式(13)所示：

Regretca=dcacs-dcacf;ca,cf,cs∈C

(13)

其中dcacs、dcacf分别表示用户ca与距用户ca第二近的司机cs之间的距离和距用户ca最近的司机cf之间的距离。把这些用户按Regret值降序依次分配到人数小于车容量约束的合乘小组中，这样可以避免由于用户分配到与之距离差距较大的第二近司机的合乘小组而对初始解质量造成不好的影响。当所有的用户被分配到合乘小组中或者所有合乘小组人数均达到车容量时，该过程将停止，未被分配到合乘小组中的用户独自驾驶。

2.3 约束验证与修复

为了降低VNSA-LTCPP(Variable Neighborhood Search Algorithm-LTCPP)的复杂性，本文在用户分配期间不对式(6)～(7)的时间窗和式(8)的行驶时间约束进行检查；而是需要通过在合乘小组中每位用户充当司机时对该司机用户进行时间窗和行驶时间约束验证来检验初始解决方案的可行性。如果合乘小组中有用户违反时间窗和行驶时间约束条件，则对该合乘小组Pr进行修复，即将该合乘小组Pr分割成包含若干个符合时间窗和行驶时间约束条件的合乘小组的合乘小组集合Sr={P1,P2,…,Pn},如式(14)～(15)所示，其中Sr中的各个合乘小组之间用户互不相同，并且Sr满足式(16)的目标函数。

P1∪P2∪…∪Pn=Pr

(14)

P1∩P2∩…∩Pn=∅

(15)

(16)

3 变邻域搜索

3.1 邻域设计

为了能够得到LTCPP的高质量解决方案，本文设计了具体的邻域搜索操作对初始解方案进行优化。邻域搜索定义如下。

1)交换邻域。

交换邻域操作每次选择两个来自于不同合乘小组的用户cx1和cy1,如果将这两个用户交换到对方的合乘小组中，形成的两个新的合乘小组人数均满足式(5)的车容量约束，则交换邻域操作成功，将这两个用户进行交换；否则这两个用户不能交换到对方的合乘小组中，交换邻域搜索结束。该邻域搜索设定20次局部优化，每次局部优化后进行一次结果评估，对合乘用户发生变化的合乘小组进行时间窗和行驶时间约束验证并进行成本评估。若局部优化后出行成本没有降低则该邻域搜索结束，否则进行下一次局部优化。该过程的示意图如图2所示，用户16与用户21在满足车容量约束的条件下互换到对方的合乘小组中。该操作的复杂度为O(n)。

图2 交换邻域示意图Fig. 2 Schematic diagram of exchange neighborhood

2)链式邻域。

a)构建一个合乘小组循环链表L,随机在S中选择一个合乘小组Pi作为L的第一个元素，并从S中删除Pi。

b)在S中选出与L中第一个插入的合乘小组Pl重心距离差wd最小的合乘小组Pf插入L中，然后从S中删除Pf。其中重心坐标(wx,wy)的计算如式(17)所示。重心距离差wd的计算如式(18)所示。

(17)

(18)

c)重复步骤b)直到中S所有的合乘小组全部插入到L中。

d)在L中选出一个合乘小组PL1作为起始点。

e)PL1中满足式(19)的用户被移动到L中的下一节点的合乘小组PL2中。

(19)

f)若当前操作节点的合乘小组人数违反车容量约束，则将该合乘小组中符合式(17)的用户从当前操作节点的合乘小组移动到当前节点的下一节点合乘小组中，并将操作节点移动到下一节点，再次执行步骤f)操作;否则链式邻域操作结束。

该邻域搜索设定50次局部优化，每次局部优化后进行一次结果评估，对合乘用户发生变化的合乘小组进行时间窗和行驶时间约束验证并进行成本评估。若局部优化后出行成本没有降低，则该邻域搜索结束；否则进行下一次局部优化。

链式邻域的示意图如图3所示，合乘小组PL1中离合乘小组重心最远的用户14被移动到L中的下一节点的合乘小组PL2中，由于新的合乘小组PL2人数超过车容量约束，故选出离该合乘小组重心最远的用户11移动到L中PL2的下一节点的合乘小组PL3,新的合乘小组PL3满足车容量约束，该操作结束。该操作的复杂度为O(n)。

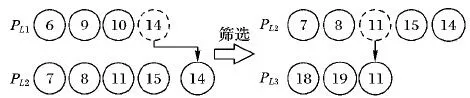
图3 链式邻域示意图Fig. 3 Schematic diagram of chain neighborhood

3)切割邻域。

切割邻域操作每次可将任意一个非单独驾车的合乘小组Pg分成两个非空的合乘小组Pg1和Pg2。对合乘小组Pg1和Pg2进行成本评估。若出行成本没有降低，则合乘小组Pg不能进行切割操作。切割邻域的示意图如图4所示。该操作的复杂度为O(1)。

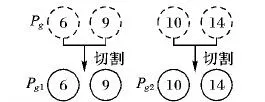
图4 切割邻域示意图Fig. 4 Schematic diagram of cut neighborhood

4)合并邻域。

合并邻域操作每次可随机选择并合并任意两个人数小于车容量约束的合乘小组Pd1和Pd2,如果合并后的合乘小组Pcb人数满足式(5)的车容量约束，则合乘小组合并初步成功；否则合乘小组Pd1与合乘小组Pd2不能合并。若合乘小组合并初步成功，对合乘小组Pcb进行时间窗和行驶时间约束验证并进行成本评估，若成本降低，则合乘小组Pd1与合乘小组Pd2最终合并成功；否则合乘小组Pd1与合乘小组Pd2不能合并。合并邻域的示意图如图5所示，包含用户2和用户3的合乘小组Pd1与包含用户4和用户5的合乘小组Pd2的人数都没有达到车容量约束，故将这两个合乘小组合并成一个合乘小组Pcb,最后通过验证合乘小组Pcb的车容量约束来判断合乘小组Pd1与合乘小组Pd2是否能够合并。该操作的复杂度是O(1)。

图5 合并邻域示意图Fig. 5 Schematic diagram of combine neighborhood

3.2 结果评估

目标函数的评估通常是启发式算法中最耗时的操作。对于LTCPP所涉及的结果评估包括成本的计算。在结果评估之前首先要验证合乘小组的时间窗和行驶时间约束，对于合乘小组中用户不满足式(6)、(7)的时间窗和式(8)的行驶时间约束的合乘小组要进行修复，其修复方法与初始解决方案的构建中使用的修复方法相同，其中切割邻域不需要对合乘小组中用户进行时间窗和行驶时间约束验证。

传统成本评估需要计算当前方案S的总花费和邻域操作前后的解决方案S1的总花费，S和S1总花费计算如式(20)、(21)所示，这样会浪费大量的计算时间，由于S1与S仅部分合乘小组用户发生变化，本文设计了一种有效的方法来对VNSA-LTCPP提供的解决方案进行评估。这种评估仅应用于邻域操作后小组成员发生变化的合乘小组，S′为发生变化的合乘小组在邻域操作前的原合乘小组集合，S"为邻域操作后发生变化的合乘小组集合。成本评估如式(22)、(23)所示。这种增量评估及其复杂性取决于目标优化问题所使用的邻域操作。其中交换、切割和合并邻域操作只评估两个变换的合乘小组。对于链式邻域操作，变换的合乘小组数量由实际的邻域操作所决定。由于减少了评估对象的数量，这种评估方法可以大幅提高VNSA-LTCPP的求解效率。

f1=∑cost(i);i∈S

(20)

f2=∑cost(j);j∈S1

(21)

f3=∑cost(k);k∈S′,S′⊂S

(22)

f4=∑cost(k1);k1∈S",S"⊂S1

(23)

3.3 VNSA-LTCPP求解过程

VNSA-LTCPP求解过程依次应用交换邻域(Exchange Neighborhood)、链式邻域(Chain Neighborhood)、切割邻域(Cut Neighborhood)、合并邻域(Combine Neighborhood)这四个邻域搜索操作。VNSA-LTCPP求解具体流程如下：

1)首先求解出初始合乘方案S0,对S0进行约束验证与修复得到S。设置迭代次数i为0。

2)对S进行交换邻域操作，每次操作完成后对新生成的合乘方案进行约束验证与修复并进行结果评估得到S1,若出行总花费没有降低则执行步骤3)；否则用S1替代S,重新对S进行步骤2)操作，直至操作次数达到该邻域操作规定的局部优化次数。

3)对S进行链式邻域操作，每次操作完成后对新生成的合乘方案进行约束验证与修复并进行结果评估得到S1,若出行总花费没有降低则执行步骤4)；否则用S1替代S,重新对S进行步骤3)操作，直至操作次数达到该邻域操作规定的局部优化次数。

4)对S进行切割邻域操作，操作完成后对新生成的合乘方案进行结果评估得到S1,若出行总花费降低则将S1替代S。

5)对S进行合并邻域操作，操作完成后对新生成的合乘方案进行约束验证与修复并进行结果评估得到S1,若出行总花费降低则将S1替代S。

6)若迭代次数i达到规定的迭代次数，则VNSA-LTCPP求解过程结束；否则迭代次数i加1，转到步骤2)。

4 实验

4.1 测试环境

软件环境为Java虚拟机SUN JDK1.8.0_111，硬件环境为64位Windows10系统,Intel Core i7 2.5 GHz CPU,8 GB RAM。

4.2 实验算例

本文所用的算例是在Solomon车辆路径问题(Vehicle Routing Problem，VRP)实例基础上修改得到的。实验算例规模分别为100人、200人、400人和1 000人，每个规模的算例各有五组，分别为S1-1、S1-2、S1-3、S1-4、S1-5；S2-1、S2-2、S2-3、S2-4、S2-5；S3-1、S3-2、S3-3、S3-4、S3-5；S4-1、S4-2、S4-3、S4-4、S4-5。由于篇幅原因，在此只列出S1-1的用户地理坐标点分布图，如图6所示。

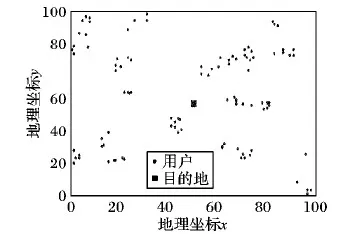
图6 用户地理坐标点分布示意图Fig. 6 Schematic diagram of user geographic coordinate distribution

4.3 实验结果与分析

本文对于S1、S2、S3和S4四种规模算例设定1 000～10 000 十个不同的HVNSA-LTCPP求解迭代次数进行实验。其中影响因子λ和μ分别设定为0.8和0.2。每组算例的实验次数均为10。

为了验证计算时间与迭代次数和算例规模之间的关系，本文对于每种规模算例的平均计算时间进行分析，其中每种规模算例的平均计算时间为每种规模5组算例的平均计算时间。从图7可以看出，当算例规模一定时，计算时间随着迭代次数的增加而增长，同时计算时间的增长速率随着迭代次数的增加而趋缓，这是由于随着迭代次数的增加，合乘方案的质量逐步提高，邻域搜索中的交换邻域和链式邻域的局部优化概率降低，对应的邻域搜索时间会减少。当迭代次数一定时，计算时间会随着算例规模的增长而增长，时间增长速率约为算例规模增长速率的80%～90%，因此对于1 000人以上的较大规模算例HVNSA仍具有一定的时效性。

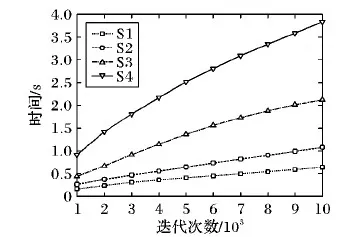
图7 算例时间趋势图Fig. 7 Trend diagram of instances’ time

本文列出S1-1、S2-1、S3-1和S4-1四组算例的部分实验数据，如表1所示。表1中：Ravg表示实验运行的结果平均值；Ropt表示算例的最优解；Eavg表示算例的平均误差；T表示计算时间。其中：100人、200人规模算例的最低出行成本由Cplex平台计算得出，400人算例和1 000人算例由于算例规模较大无法在合理时间内通过Cplex平台计算出算例的最低出行成本。S2-1的部分合乘小组接送顺序分配结果如下所示：

第一组：197→13→58→73;58→197→13→73;13→197→58→73;73→58→197→13。

第二组：129→95→96→195;95→129→96→195;195→96→95→129;96→195→95→129。

第三组：119→27→191→18;18→191→27→119;191→18→27→119;27→191→18→119。

第四组：39→151→168→152;168→152→39→151;151→39→168→152;152→168→39→151。

第五组：88→104→20→14;20→88→104→14;14→20→88→104;104→88→20→14。

其中，对于每个用户所分配接送顺序所行驶的路径都是该用户接送其他用户到达目的地的最短路径，例如第一组的用户197按照顺序接用户13、58和73最后到达目的地，用户197按照这个顺序所行驶的路径最短。

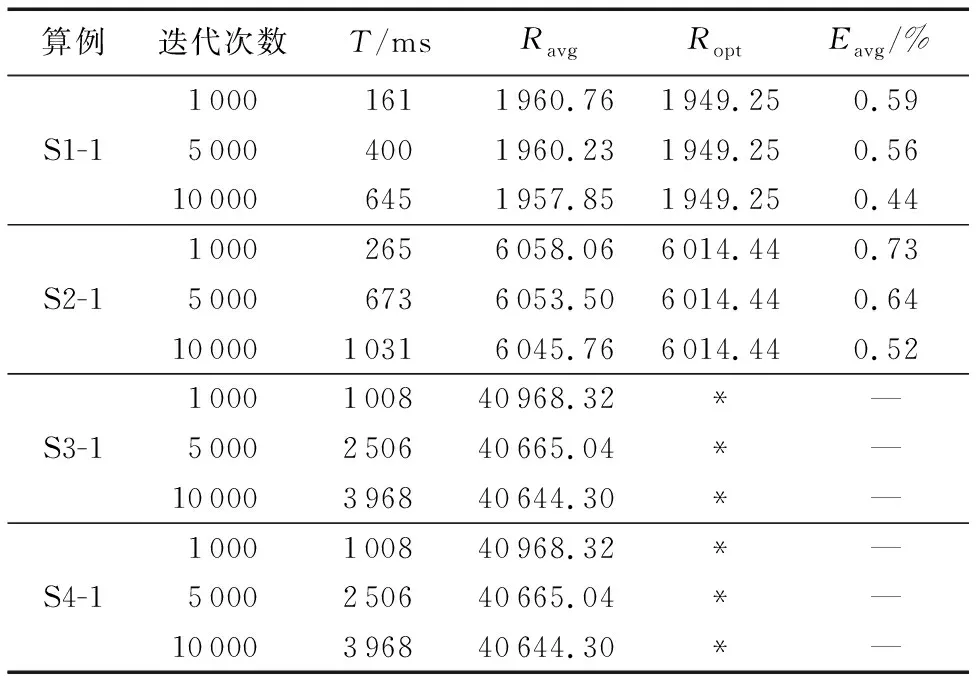
表1 S1-1、S2-1、S3-1和S4-1的计算结果Tab. 1 Calculation results of S1-1, S2-1, S3-1 and S4-1

从表1中可以看出：算例S1-1，S2-1平均出行成本均接近算例的最优出行成本；随着迭代次数的增加，初始解方案得到局部优化的次数也随之增加，实验计算出的出行成本也随之降低。

为了验证算法的有效性，这里对四种规模的20组实验算例进行实验，并与遗传算法(Genetic Algorithm, GA)和蚁群算法(Ant Colony Algorithm, ACA)的实验结果比较，实验数据如表2所示。HVNSA的迭代次数设定为10 000，由于算法不同，故通过一定的迭代次数来验证三种算法在求解时间和求解质量上的优劣无法保证公平性。本文采用HVNSA求解质量作为终止条件来比较三种算法计算时间的对比方案。其中：T表示计算时间；Rmax表示实验运行结果的最大值；Rmin表示实验运行结果的最小值；Eavg表示HVNSA的平均误差；TGA表示HVNSA计算时间与GA计算时间的比值；TACA表示HVNSA计算时间与ACA计算时间的比值。

由表2的结果分析可得HVNSA对于求解LTCPP具有很高的时效性和可靠的求解精度，能够在短时间内求解出高质量的合乘方案。其中：100人规模的算例平均误差在0.41%左右，200人规模的算例平均误差在0.58%左右。在相同求解质量条件下，HVNSA的计算时间比GA和ACA的计算时间均大幅减少，并且随着算例规模的增长，计算时间减少的幅度更大。

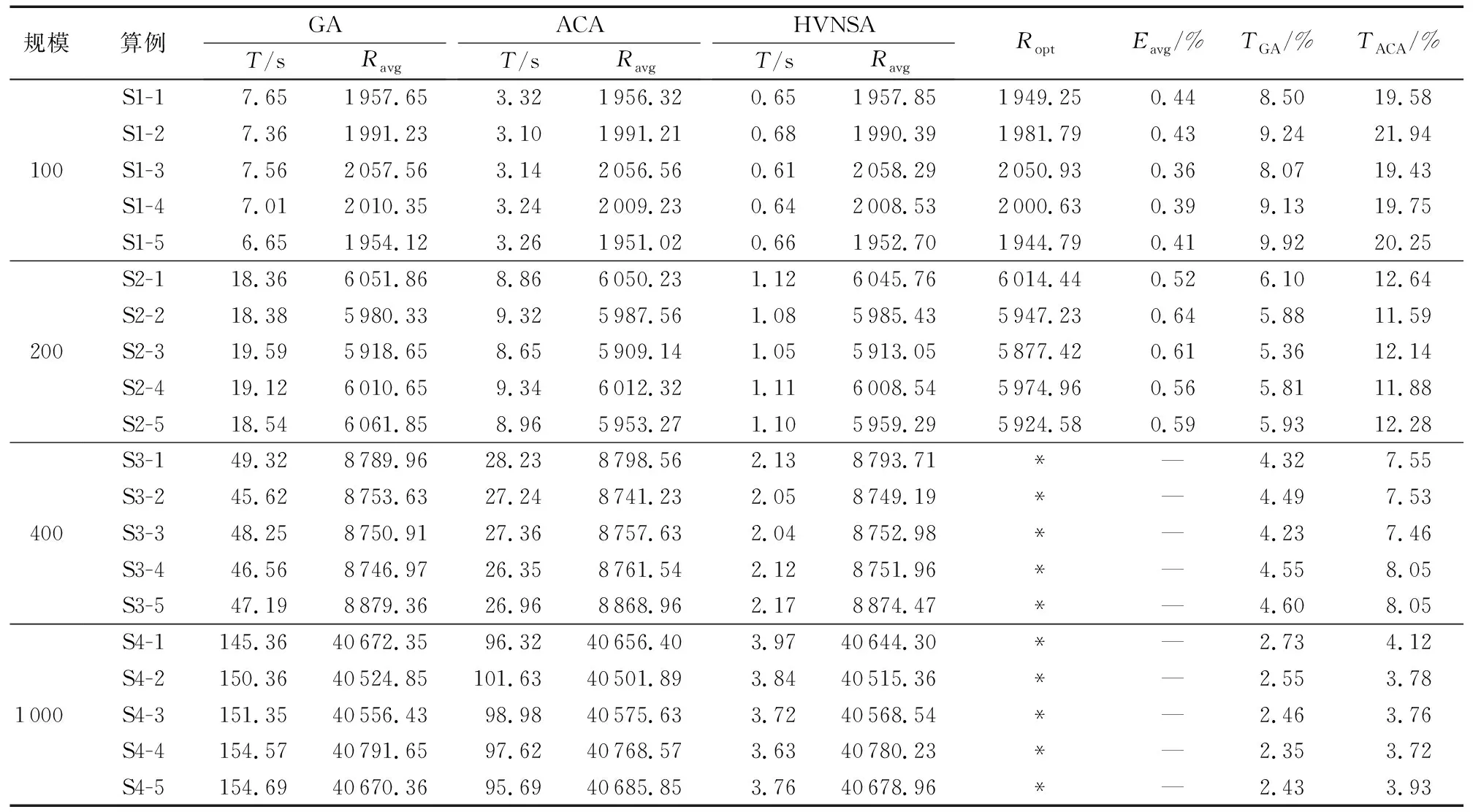
表2 四种规模算例的计算结果Tab. 2 Calculation results of four scale examples

5 结语

本文构建了LTCPP模型，并且提出了基于启发式算法的变邻域搜索算法。通过实验对比分析，该算法在计算速度上对于遗传算法和蚁群算法具有明显的优势，能够在短时间内产生高质量的长期车辆合乘方案，对于缓解交通拥堵、降低人们出行成本具有很高的实用性。将来的研究可以结合分布式计算在相同计算时间内生成更优的合乘方案，此外引入用户的偏好和环境影响因素等约束也是将来研究的一个方向。