基于混沌映射的多因子认证密钥协商协议

王松伟,陈建华

(武汉大学 数学与统计学院,武汉 430072)(*通信作者电子邮箱wangsw_ecc@163.com)

0 引言

随着互联网各种应用需求的快速增长,网络广泛应用于商业、交通、政务、娱乐、医疗等领域,如医生通过远程医疗信息系统可以给患者提供方便快捷的电子医疗服务,同时由于网络的开放性,病人的医疗记录等隐私需要保护以避免信息泄露。为了保护用户的安全和隐私,近年来海内外学者提出了一系列协议。比如,基于口令的单因子认证协议[1],基于口令+智能卡的双因子认证协议[2],基于口令+智能卡+生物特征的多因子认证协议[3]。

2013年Guo等[4]提出了一个基于智能卡的认证协议,随后Hao等[5]指出其不能保护用户匿名性,并提出了一个新的认证协议。但是Lee[6]和Jiang等[7]指出Hao等[5]不能抵抗智能卡丢失攻击和Bergamo攻击[8]等问题。2014年,Xu等[9]提出了一个基于椭圆曲线的远程用户认证方案。随后,Mishra[10]指出Xu协议[9]在登录和认证阶段存在设计漏洞,接着2015年Amin等[11]发现Xu方案[9]口令修改效率低下,并提出一个新的协议。2016年Zhang等[3]提出了一种基于混沌映射的认证密钥协商协议,接着王彩芬等[12]通过分析Zhang等[3]方案,发现并不能抵抗内部攻击。Park等[13]提出的基于椭圆曲线的三因子认证协议,也被发现无法提供用户匿名性且存在字典攻击；Jung等[14]提出的匿名认证协议则无法保护用户匿名性，存在字典攻击、内部攻击且不具备前向安全性；Jiang等[15]提出的三因子认证协议也无法保护用户匿名性，不能提供前向安全性且存在字典攻击。针对以上问题,Wang等[16-18]指出设计实现用户匿名性或多因子安全性的身份认证协议,必须采用公钥密码技术。传统的公钥密码技术主要基于以下数学难题:大整数因子分解难题、离散对数难题、椭圆曲线离散对数难题。由于切比雪夫多项式混沌映射相比传统公钥算法具有较高的计算效率,2017年Li等[19]提出了一个更安全的基于混沌映射的医疗信息系统远程用户认证方案。

本文简单回顾文献[19]的方案并指出其不能抵抗用户冒充攻击,容易遭受拒绝服务攻击,且无法确保用户身份唯一性。本文提出了一个基于混沌映射的三因子认证密钥协商协议方案,最后对协议进行安全性分析和性能分析,并与已有协议进行比较,表明本文协议更加安全高效和实用。

1 预备知识

1.1 切比雪夫多项式

定义1 切比雪夫多项式[20]。设n为正整数,x∈[-1,1],n阶切比雪夫多项式Tn(x)定义如下:

Tn(x)=cos(n×arccos(x))

(1)

此外,切比雪夫多项式还有一种等价的递归定义如下:

Tn(x)=2xTn-1(x)-Tn-2(x)

(2)

其中：n≥2,T0(x)=1,T1(x)=x。

性质1 半群性质[8]:

Tr(Ts(x))=Trs(x)=Tsr(x)=Ts(Tr(x));r,s∈N

(3)

2008年,Zhang[21]证明了切比雪夫多项式在区间(-∞,+∞)上仍然具有半群特性。

定义2 扩展切比雪夫多项式。设n为正整数,x∈(-∞,+∞),则定义在区间(-∞,+∞)上的n阶扩展切比雪夫多项式Tn(x)为:

Tn(x)=cos(n×arccos(x)) modp

(4)

其等价的递归定义:

Tn(x)=2xTn-1(x)-Tn-2(x)(modp)

(5)

其中:n≥2且p是一个大素数。这里T0(x)=1,T1(x)=xmodp。显然,式(5)同样具有半群性质,即:

Tr(Ts(x))≡Trs(x)≡Tsr(x)≡Ts(Tr(x))(modp)；

r,s∈N

(6)

1.2 切比雪夫多项式数学难题

多项式时间内求解以下问题是困难的[21]:

问题1 混沌映射离散对数问题。给定x,p,以及y=Tr(x)(modp),找到一个正整数r,使得Tr(x)(modp)≡y。

问题2 混沌映射计算Diffie-Hellman问题:给定p,x,以及Tr(x)(modp)和Ts(x)(modp),找到一个正整数y,使得Trs(x)(modp)≡y。

1.3 模糊提取器

生物特征如指纹、脸、虹膜、掌纹等,具有普遍性、唯一性、稳定性、识别率高和不可复制等特性,因而成为个人身份鉴别与识别的重要依据,在密码协议中得到广泛应用[13-15,22]。 Dodis等[23]提出的模糊提取器很好地解决了生物特征应用中的难题;当两次输入的BIO′和BIO相差不大时,模糊提取器可以输出一个一致的随机字符串σ。服务器等设备只需存储随机字符串σ,而无需存储用户生物特征。

模糊提取器可用算法函数〈Gen,Rep〉表示:Gen是一个随机数生成算法函数Gen(BIO)=(σ,θ),当输入生物特征BIO时,Gen将输出一个随机字符串σ和一个辅助随机字符串θ,其中:σ为安全参数;Rep是一个随机恢复算法函数σ=Rep(BIO′,θ)。模糊提取器在接收到一个误差允许范围内的生物特征BIO′以及相应的随机辅助字符串θ时,若dis(BIO′,BIO)≤ε,则恢复出对应的字符串σ,其中：dis(BIO′,BIO)≤ε表示BIO′和BIO的距离不超过一个给定的区间ε。

2 Li协议方案

本章对Li协议[19]作一个简单的回顾。

表1 Li协议[19]中到的符号说明Tab. 1 Symbol description of Li protocol[19]

2.1 注册阶段

1)用户Ui选取身份IDi和口令PWi,通过安全信道发送IDi给服务器S。

2)服务器生成随机数ei并计算CIDi=h(IDi,ei),B0=h(CIDi,s),通过安全通道发送B0,CIDi给Ui。

3)用户选取随机数bi,计算HPWi=h(PWi,bi),B1=B0⨁h(IDi,HPWi),B2=h(IDi,PWi)⨁bi,并将数据(B1,B2,CIDi)存储到移动设备中。

2.2 登录阶段

1)用户Ui输入用户名IDi和密码PWi,计算bi=B2⨁h(IDi,PWi),HPWi=h(PWi,bi)。

2)用户选取随机数u、ri,计算C1=B1⨁h(IDi,HPWi)⨁ri,C2=Tu(x),C3=h(ri)⨁IDi,C4=h(IDi,CIDi,ri,C2,C3),通过公共信道发送M1={CIDi,C1,C2,C3,C4}给S。

2.3 认证阶段

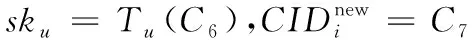
3 Li协议的安全性分析

3.1 用户冒充攻击

3.2 拒绝服务攻击

3.3 无法确保用户身份唯一性

在实际中,很有可能两个不同用户选择了相同的身份,按照Li方案[19],这两个用户都可以注册成功,而且也都是合法用户,也可以登录同一个服务器,然而服务器却无法区分他们,这可能会产生严重问题。

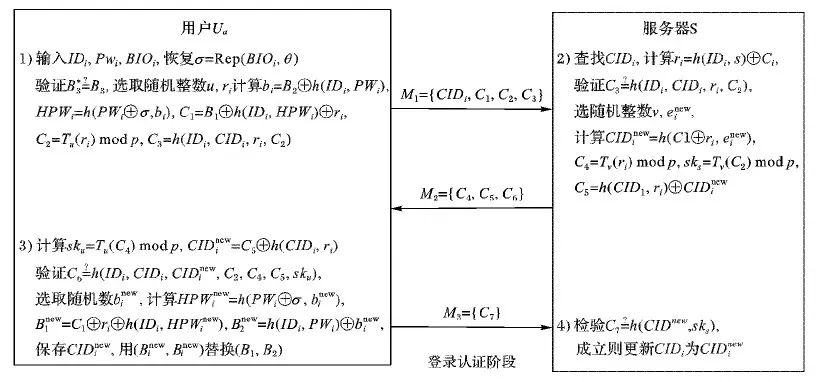
图1 新协议的认证过程Fig.1 Certification process of new protocol

4 本文协议

本文提出了一个新的基于扩展混沌映射的三因子认证协议。新协议包括:注册、登录认证、口令修改以及注销等四个阶段。相关符号的含义如表2所示。

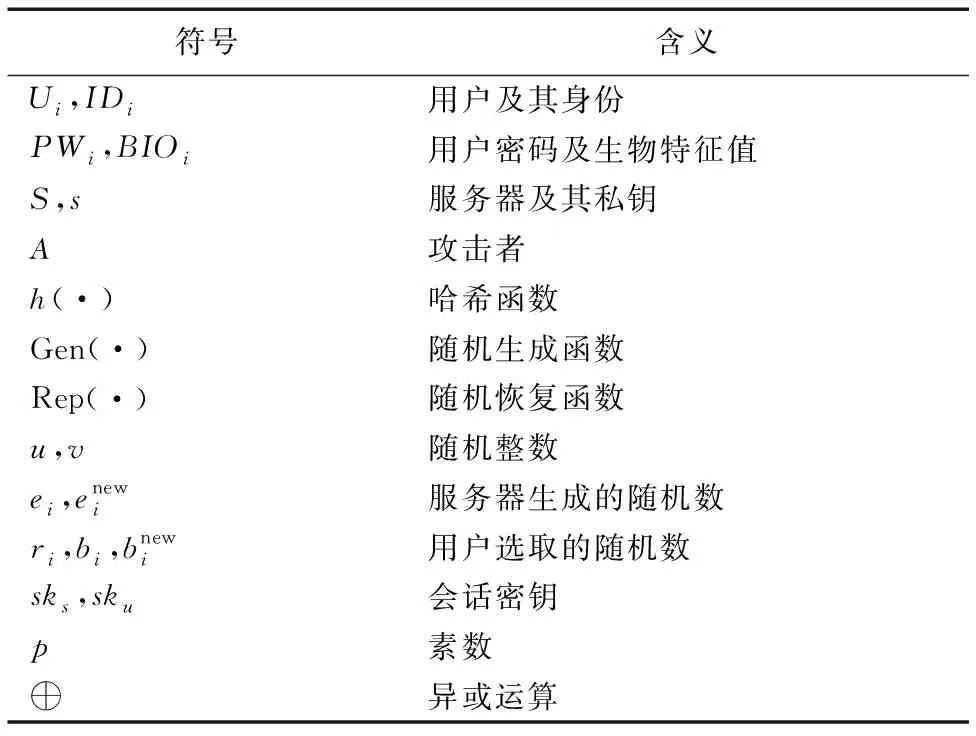
表2 本文协议中的符号说明Tab. 2 Symbol description of the proposed protocol

4.1 注册阶段

1)用户Ui选取身份IDi和口令PWi,通过安全信道传送IDi、生物信息BIOi给服务器S。

2)服务器收到用户注册请求之后,首先查找IDi是否已存在,若存在,表明该ID已经被注册,拒绝用户注册请求；若不存在,将生物信息输入到模糊提取器得到一个随机字符串σ和一个辅助随机字符串θ,即Gen(BIOi)=(σ,θ)。S选取随机数ei,并计算B0=h(IDi,s),CIDi=h(B0,ei),通过安全信道发送消息B0,CIDi,θ,Rep(·),p给Ui,其中p为素数,同时在后台数据库添加(IDi,CIDi),将BIOi删除。

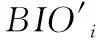
4.2 登录认证阶段

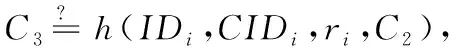
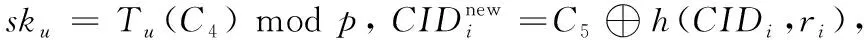
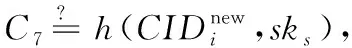
由于C2=Tu(ri) modp和C4=Tv(ri) modp,则有

sks≡Tv(C2)≡Tv(Tu(ri))≡Tvu(ri)≡

Tuv(ri)≡Tu(Tv(ri))≡Tu(C4)≡skumodp

所以本文方案是正确的。

4.3 口令修改阶段

4.4 注销阶段

当用户不再使用该服务时,Ui可以向服务器申请注销其账号,服务器在验证了用户Ui的身份之后,在用户数据库中找到其IDi,然后将(IDi,CIDi)从数据库中删除即可。

5 新协议方案分析

5.1 安全性分析假设

定义方案安全性分析的安全假设如下:

假设1 攻击者可以截获公开信道上的信息,且能够对信息进行修改和重放,攻击者获得用户的设备后可以利用能量分析等方法(Kocher等[24]、Messerges等[25]、Brier等[26])获取设备中存储的数据。

假设2 服务器的主密钥s、哈希函数是安全的,即攻击者在多项式时间内无法解决这些问题。

5.2 新协议安全性

在以上安全假设下,下面分析本文方案的安全性:新协议给每个用户分配动态身份保护用户匿名性,所以这里假设攻击者已经锁定了目标用户。

1)抵抗Bergamo攻击:Bergamo攻击[8]中,攻击者必须得到x,Tr(x)和Tk(x)三个元素,才能发动有效攻击。本文协议采用扩展的切比雪夫多项式,采用了模运算,而且x∈(-∞,+∞)能够效避免三角函数的周期性。

4)抗口令猜测攻击:本文协议没有在线对用户口令验证,而是验证用户与服务器共享的秘密值攻击者选择在线攻击时,当停止会话次数达到预先定义的阈值,账号会被锁定,所以,本文协议可以抵抗在线猜测攻击。对于离线猜测攻击,假设攻击者获得了用户的设备,即使攻击者可以同时猜测用户的身份和口令,由于B3=h(σ,IDi⨁PWi)modn,攻击者却无法验证猜测口令的正确性。

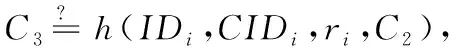
6)抗设备丢失攻击:假设攻击者获得Ui的设备,并通过能量分析获得设备中的信息(B1,B2,B3,CIDi,θ,Rep(·),p)，由以上分析可知,攻击者并不能得到用户的口令,也无法伪造用户的生物信息。

7)抗重放攻击和冒充攻击:本文协议中用户每次均采用动态身份登录,攻击者直接重放以前经过双方认证的消息很容易被识破,攻击者只能冒充合法用户或者服务器尝试构造正确的消息进行攻击。

(a)攻击者M冒充用户:假设攻击者获得了用户的移动设备并获得用户的CIDi,然后冒充用户。因为C1、C2、C3都与随机数ri有关,因此攻击者若要冒充用户,必须构造C1、C2、C3,攻击者无法获得用户的口令,更不可能获得服务器密钥s,所以很难伪造出C1。

(b)攻击者M冒充服务器:因为用户每次登录选择不同的随机数ri,显然直接重放消息M2={C4,C5,C6}无效,攻击者只能尝试构造C4、C5、C6,攻击者必须先计算出ri,而ri=h(IDi,s)⨁C1,攻击者不可能获得服务器密钥s,所以很难伪造出正确的ri。

8)中间人攻击:由以上分析可知,攻击者无法计算相关消息,简单的消息重放很容易被识破,更不可能计算出共享会话密钥。

9)完美前向安全性:本文协议双方协商的会话密钥为sks≡Tuv(ri)≡Tv(Tu(ri))≡Tu(Tv(ri)) modp,假设攻击者获得系统密钥和用户的口令,通过公开信道截获到会话密钥的两个元素Tu(ri) modp和Tv(ri) modp然而攻击者在不知道随机数u或v的情况下,计算Tuv(ri)面临扩展切比雪夫多项式的数学难题,若攻击者先由Tu(ri) modp和Tv(ri) modp计算出u或v也面临扩展切比雪夫多项式的数学难题。

10)已知会话密钥安全性:已知会话密钥安全性是指通信双方产生的会话密钥之间应该相互独立。本文协议会话密钥sks≡Tuv(ri)≡Tv(Tu(ri))≡Tu(Tv(ri)) modp,其中u和v是用户和服务器选取的一次性随机数,所以即使攻击者获得了某一次的会话密钥sk,他也不可能计算出下一次的会话密钥sk′。

5.3 性能分析

本节将新协议同Xu协议[9]、Mishra协议[10]、Amin协议[11]、Zhang协议[3]、Li协议[19]进行比较。

从表3的分析结果来看,本文协议方案在功能上明显优于其他的认证协议方案。

5.4 计算效率分析

表4对比了计算效率,符号含义如下:Th表示计算一次哈希函数值所需时间;Tc表示计算一次切比雪夫多项式所需时间;Ta表示计算一次椭圆曲线点加所需时间;Te表示计算一次椭圆曲线点乘所需时间;Ts表示进行一次对称加密(或解密)所需时间。

依据文献[27]可知:Te>Ta≫Th,Tc≈70Ts≈175Th,Ts≈2.5Th。由于协议的主要运算在登录和认证阶段,所以表中仅使用这两个阶段进行性能比较。从表4的结果来看,本文方案仅需4Tc+15Th,虽然文献[10]方案比本文方案要快,但文献[10]不能抵抗重放攻击、设备丢失攻击及中间人攻击,很显然本文方案计算性能明显优于其他方案。

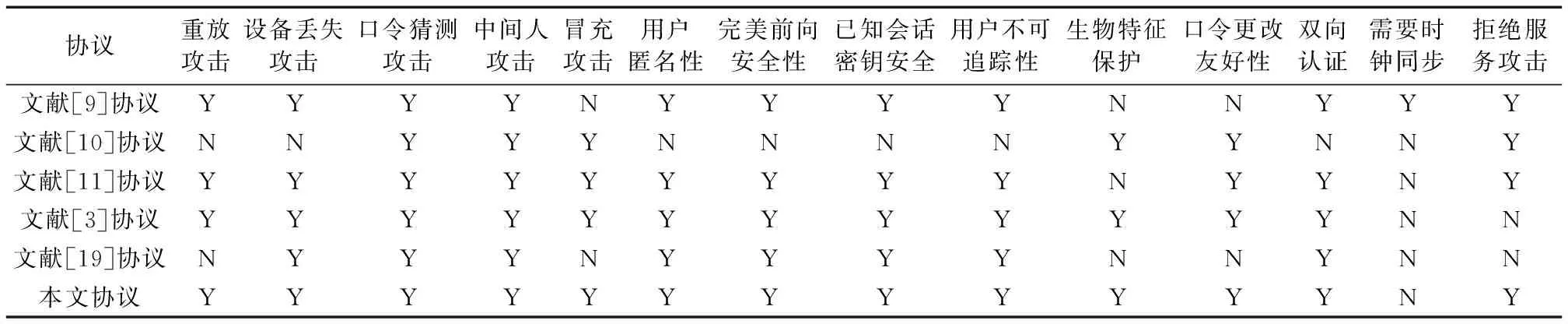
表3 不同协议的功能对比Tab. 3 Functional comparison of different protocols

表4 不同协议的计算效率对比Tab. 4 Computational efficiency comparison of different protocols

6 结语

通过分析Li方案,指出其不能抵抗用户冒充攻击,容易遭受拒绝服务攻击等缺陷。本文提出了一个三因子认证密钥协商协议,通过使用扩展混沌映射,采用三次握手技术实现异步认证,保护用户匿名性和身份唯一性,安全性分析和性能分析结果表明,新协议不仅可以抵抗常见攻击,满足必要的安全需求,还具有较高的计算效率,因此,新协议具有更高的实用性。