基于负载牵引和记忆效应的X参数的功放建模

南敬昌，樊 爽，高明明

(辽宁工程技术大学 电子与信息工程学院，辽宁 葫芦岛 125105)(*通信作者电子邮箱1437453960@qq.com)

0 引言

近年来，无线通信系统的飞速发展对于通信的质量和效率提出了非常高的要求。作为无线通信的主要器件，射频功率放大器对于通信系统有着重要影响，研究射频功率放大器的各项性能指标成为电子与信息系统的科研方向和热点问题。如何更精准地表征功率放大器的非线性特性以及记忆效应，使其能够方便地应用于系统级仿真，提高模型的精确度，成为研究功放行为模型的重要问题。

行为模型理论能够较高精度地完成仿真计算，同时能够精确地展现出系统的非线性效应。一般来讲，行为模型的建立过程都起始于实际测量与仿真结果，辅以合理的物理假设与参数化辨识方法，进而得到完整的模型参数与框架。其中非线性X参数模型作为下一代工业级别标准化非线性行为模型方法，能够准确表征复杂频谱分布下有源器件的性能响应，逐渐成为当前微波工程的研究热点[1]。

功率放大器的行为建模是利用输入输出数据来建立描述其行为特性的数学模型的方法和技术，它为分析和评估通信系统质量，设计数字预失真线性化模块等相关科研活动提供了一种方便而有效的途径[2]。表征功放记忆效应的行为模型现主要有Volterra级数模型、神经网络模型和X参数模型。其中Volterra级数模型及其多项式的功放模型能够准确描述功放特性[3]，但当Volterra级数模型在多器件系统或级联非线性框图中运用时，超大的计算量限制了它在工业化中的进一步推广。神经网络模型拥有较强的学习能力和逼近能力，然而模型的泛化能力不强，难以由硬件实现。X参数模型是对经典S参数模型的严格数学扩展，有着严谨的理论基础，工程师通过X参数模型能够实现任意射频器件从行为模型提取、电路搭建、仿真设计、性能优化、版图制作以及性能测试的完整流程[4]。它最大的优点是容易理解且易于级联，考虑共轭信号的影响，表征精度高，能够描述在大信号作用下的非线性网络产生的互调失真和频谱再生[5]。将X参数模型用于表征功放的记忆效应，其研究意义十分重大。

近年来关于X参数在微波射频领域的研究备受关注。文献[6]中提出了多谐波失真(Poly Harmonic Distortion， PHD)模型，随后安捷伦科技公司将PHD模型申请为专利商标，运用该公司的PNA-X系列非线性矢量网络分析仪搭建完成NVNA硬件测量平台[7-8]。但PHD模型只能够表征只有一个大的射频输入信号而忽略其他小信号的情况，功率放大器在基本匹配的情况下功放的非线性行为，当出现由于负载阻抗引起的细小偏差而导致输出端口不匹配时，此时基波与谐波将会产生反射，这导致了传统的静态X模型仿真精确度较低。文献[9]中首次提出动态X参数模型，并引入了表征长期记忆效应的三维核函数，但三维核函数的提取及验证都极为困难。文献[10]中提出基于前馈(Feed-Forward, FF)结构的动态X参数模型，提出一种表征功放记忆效应的新方法，但模型仅考虑功放的长期记忆效应，参数辨识困难且普适性差。文献[11]中提出将输出信号为幅度与频率双变量的新型反馈(FeedBack, FB)结构引入时变频率变量而简化动态核函数为二维核函数，模型的精度有了一定提高，但没有考虑模型在谐波失配情况下产生的扰动，模型仿真速度较慢。

针对以上问题，本文提出了一种新型的X参数建模方法。首先引入负载反射系数|ΓL|，结合X参数模型，构建大信号与二端口信号的二维函数以提高模型的准确度；但由于二维核函数的复杂性，且验证和应用都比较困难，使用仅保留负载反射系数的幅度信息的一维扫描代替二维核函数的提取。对于X参数表达式中的动态核函数，选用改进的FF模型来代替，FF模型将功放的记忆效应分为短期记忆效应和长期记忆效应，提取出FF模型中表征功放长期记忆效应的核函数，将其用于代替X参数表达式中的动态部分以考虑功放的记忆效应，提取方法使用阶跃信号[12]代替原始的双音信号对提取方法进行简化。新的动态X参数模型与静态X参数模型、传统的动态X参数模型、FF结构X参数模型以及FB结构的X参数模型相比，不仅具有较高的精确度，而且与FF结构模型和FB结构模型仿真相比，仿真时间均有所提高。

1 模型分析

1.1 散射函数

散射函数[13]描述的是被测器件出射波和入射波基波及各次谐波之间的映射关系：

Bpm=Fpm(A11,A12,…,A21,A22,…)

(1)

其中:B表示出射波；A表示入射波；p表示端口号；m表示谐波次数。

1.2 静态X参数模型

为进一步化简模型，对散射函数进行一阶Taylor级数展开，结合谐波叠加原理，PHD模型[14]如下：

(2)

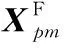
1.3 动态X参数模型

动态X参数模型[15]是在静态X参数模型的基础上延伸得到的，引入了能够表征时变系统的“动态”部分。这里假设一个完美匹配的网络，只有一个输入基波分量A(t)，相应的只有一个输出基波量B(t)，不考虑谐波分量的影响。另外，假设输出端口阻抗匹配。动态X参数模型的表达式如下：

B(t)=FCW(|A(t)|)·exp(jφ(A(t))+

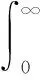
(3)

∀x,u:G(x,x,u)=0

(4)

该模型的基本理念在于将输出包络信号B(t)分解为稳态部分和动态部分，稳态响应部分即由非线性响应FCW(|A(t)|)激励输出当前时刻的复包络，动态部分由记忆核函数G(·)在各时间点的叠加组成。其中，FCW(|A(t)|)和G(·)都只是输入信号A(t)瞬时幅值的函数，因而输入信号的相位信息作为一个独立的分量和幅度信息相乘，引入Φ(t)=exp(jφ(A(t)))。稳态部分和经典的PHD模型输出相同，动态部分反映了长期记忆效应的作用。能够反映记忆效应的三维记忆核函数G(·)，其数值只取决于三个因素：时间间隔u、当前时刻输入复包络的瞬时幅度A(t)和过去u时段的输入复包络幅度A(t-u)。

1.4 |Γ21|模型

对于如式(2)所示PHD模型，只有在放大器近乎完全匹配的情况下才能给出很好的预测，即确保|Γ21|≪1，此时|A21|足够小。因此，在匹配良好的情况下，在大信号工作点(Large-Signal Operating Point, LSOP)[16]下的被测器件的入射信号A21可以忽略不计。此时包含直流偏置DCbias的LSOP为：

LSOPbasic=(DCbias,|A11|)

(5)

然而，当放大器出现不匹配的情况时，PHD模型将不能准确预测整个Smith圆图上的行为，因为在PHD中，散射波B21只与基波输入的大信号激励|A11|有关，此时情况比PHD模型所描述的更为复杂。

在不匹配的情况下，反射波B21将反映这种不匹配，并在输出端口产生入射波A21，条件|Γ21|≪1不再满足，这时A21足以改变被测器件的LSOP，此时先前使用的频谱近似无效。

传统的负载牵引模型提出将|A11|与负载反射系数Γ21结合以解决这一问题，此时负载牵引模型的LSOP为：

LSOPloadpull=(DCbias,|A11|,Γ21)

(6)

1.5 FF结构模型

假设功放输入信号为一个恒定包络的大信号A0与变包络的小信号A1的叠加：

A(t)=Re(A0·ejω0t+A1·ej(ω0+Ω)t)

(7)

FF结构模型拓扑结构[17]如图1所示，A(t)表示输入信号，B(t)表示输出信号，输入和输出之间的两个路径是根据功放的电路结构建立的双记忆路径模型，即短期记忆效应(Short Term Memory, STM)与长期记忆效应(Long Term Memory, LTM)。这种拓扑结构趋向于模仿放大器电路中的两个基本内存路径，使得功放被建模为一个在FF结构中有长期响应调制的系统。该模型结构中STM路径的作用是捕获功放主动态，担当着放大以及滤波的作用，当一个时变包络信号通过这条路径时，STM路径的短期非线性作用将会产生一个低频信号反馈到LTM路径中，LTM路径本身是动态非线性的，它可以看作是一个对放大器直流静态点缓慢调节的过程，以偏置网络的速率进行充放电，使器件自行加热或捕获动态，进而影响STM路径。该模型的表达式如式(8)所示:

B(t)=(1+BLT(t))·BST(t)

(8)

其中：

(9)

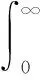
(10)

(11)

(12)

图1 FF结构模型拓扑Fig. 1 Topology of FF structural model

2 |Γ21|-X参数模型

传统的二维负载牵引模型需要覆盖整个Smith圆图，且只能使放大器在大信号下的工作区域局限于Smith圆图上的一点，这种方法会增加文件大小，使模型维度升高。而|Γ21|模型将负载反射幅度|Γ21|与|A11|相结合，运用二次谐波失真(Quadratic Poly-Harmonic Distortion，QPHD)模型[18]，使放大器在大信号下的工作区域变为由参数|Γ21|控制的在Smith圆图上的一个圆，且由|Γ21|完全取代Γ21，在保证精确度的情况下，使只保留负载反射幅度的一维模型代替复杂的二维模型。

本文从理论出发，在X参数动态模型中引入该负载牵引模型以对传统的动态X参数模型的建模方法进行改进，新的X参数建模方案不仅能够保证精确度，还能够得到简化的模型文件。将新的X参数模型用于进行放大器记忆核函数的提取，在提取方法上，将传统的双音大激励输入信号替换为窄带阶跃信号以简化模型的提取过程[19]。

将|Γ21|模型中的大信号工作区域命名为参数控制的大信号工作圆(Parametric Large-Signal Operating Circle， PLSOC)，其模型如下：

RPLSOC=(DCbias,|A11|,|Γ21|)

(13)

2.1 |Γ21|-静态X参数模型

通过引入参数|Γ21|，对QPHD负载牵引模型进行简化，得到改进的静态X参数模型为：

Bpm=Fpm(|A11|,|Γ21|)pm+

(14)

2.2 |Γ21|-动态X参数模型

根据上述结论和X参数模型基础理论，参数|Γ21|牵引下的非线性电路或系统的行为模型可以表示为：

B(t)=F(|A(t)|,|Γ21|)Φ(t)

(15)

文献[20]中用h1(t)，h2(t)，…，hN(t)等多个隐含变量来表示记忆效应对系统的映射关系。结合式(15)，通过这种方式所建立的带有记忆效应的非线性电路或系统的行为模型可以表示为式(16)：

B(t)=F[(|A(t)|,|Γ21|),h1(t),h2(t),…,

hN(t)]Φ(t)

(16)

通过先验信息和物理测试设备，可以获得输入信号和隐含变量之间的关系为：

(17)

将式(17)中的隐含变量看作是通过线性滤波器得到的，即冲击响应ki(·)与非线性函数Pi(·)的卷积，则式(17)表明了一种特殊的非线性关系。为了更好地完成线性化过程，设输入信号的幅度始终保持不变，即|A(t-u)|=|A(t)|=X，则式(17)可以整理为：

(18)

其中：

(19)

将式(18)代入式(16)中可得：

B(t)=F[(|A(t)|,|Γ21|),W1P1(|A(t)|,|Γ21|)+

Δ1(t),W2P2(|A(t)|,|Γ21|)+Δ2(t),…,

WnPn(|A(t)|,|Γ21|)+Δn(t)]·Φ(t)

(20)

其中：

∀i:Δi(t)=hi(t)-W1P1(|A(t)|,|Γ21|)

(21)

式(20)中所带的偏差量Δi(t)可以修正hi(t)，使其更接近实际值。对式(20)继续进行线性化：

B(t)=F[(|A(t)|,|Γ21|),W1P1(|A(t)|,|Γ21|),

(22)

其中：

(23)

函数Di(·)表示输出信号对隐含变量变化的反应。假设h1(·)代表温度，那么D1(·)代表温度的变化对输出信号的影响。引入函数FCW(·)，可表示为式(24)：

FCW(|A(t)|,|Γ21|)=F[(|A(t)|,|Γ21|),

W1P1(|A(t)|,|Γ21|),W2P2(|A(t)|,|Γ21|),…]

(24)

将式(24)代入式(22)，式(22)可简化为：

B(t)=FCW(|A(t)|,|Γ21|)·Φ(t)+

(25)

式(25)中，从结构上分为两部分：一是由函数FCW(·)代表的静态部分，其他部分表示动态部分。由式(24)表示的静态部分，对应典型的PHD模型。因此，下标“CW”代表被测件在单一信号连续波下的激励响应。

将式(21)代入式(25)，可得到式(26)：

B(t)=FCW(|A(t)|,|Γ21|)·Φ(t)+

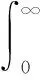
(26)

注意到：

(27)

因此，式(27)可以写作：

B(t)=FCW(|A(t)|,|Γ21|)·Φ(t)-

(Pi(|A(t-u)|,|Γ21|)du·Φ(t)

(28)

定义多元函数G(x,y,u)如式(29)所示：

(29)

所以，式(27)可以写作：

B(t)=FCW(|A(t)|,|Γ21|)·Φ(t)+

(30)

至此，通过借助隐含变量，线性化方程得到了含有记忆效应器件的动态X参数模型，该行为模型的第一项代表了静态部分，其中FCW(·)表示静态X参数核，G(·)为记忆核。

将改进的FF结构与式(30)结合，改进的动态X参数模型为：

B(t)=FCW(|A(t)|，|Γ21|)Φ(t)+

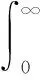
(31)

其中：

G(|A(t)|,|Γ21|,Ω)=HST(|A(t)|,|Γ21|,Ω)·

(1+HLT(|A(t)|,|Γ21|,Ω))

(32)

因为STM核函数容易通过包络恒定的调制信号进行测量，这时LTM路径效应为零。此时输入信号周期为0，即输入信号一个幅度固定为常数的单音连续信号：

A(t)=Re(A0ejΩ t)

(33)

输入信号包络幅度、负载反射系数及频率的函构成输出信号的包络，可以由式(34)表示：

B(t)=B0(|A0|,|Γ21|,Ω)ejΩ t

(34)

将式(33)和(34)代入式(31)可得输出信号为：

B(t)=(1+HLT(|A0|,|Γ21|，0))·

HST(|A0|,|Γ21|,Ω)·A0ejΩ t

(35)

由于此时LTM核函数HLT(|A0|,|Γ21|,0)为零，故STM的核函数为：

(36)

而在对LTM核函数进行提取时，功放的输入信号为：

A(t)=|A0|+|A1|ejΩ t;|A1|≤1

(37)

此时信号的包络为：

(38)

由于|A1|远小于|A0|，故功放输出端得到一个由|A0|、负载反射系数幅值|Γ21|及频率构成的三音信号，如式(39)所示：

(39)

此时，FF模型的拓扑结构可以表示为：

HST(|A(t)|,|Γ21|,Ω)=

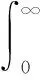
(40)

HLT1(|A(t)|,|Γ21|,Ω)=

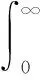
(41)

HLT2(|A(t)|,|Γ21|,Ω)=

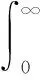
(42)

将式(39)代入式(40)并固定负载反射系数的幅值，通过测量获得输出端的信号和频率，此时LTM端信号为：

(43)

其中：

(44)

其中上标和下标分别对应于同步和反同步输出的频率分量，结合式(37)、(38)和负载反射系数，并在点A0处一阶泰勒展开可得：

hLT(|A|,|Γ21|,t)=hLT(|A|,|Γ21|,t)+

(45)

此时将式(45)代入式(41)和(42)并令其等于式(43)，通过固定频率Ω和负载反射系数幅值，使A(t)在A0点从零开始移动到无穷，使用经典欧拉算法或梯形法解微分方程得到LTM核函数为：

(46)

通过式(46)推导可以得到将|Γ21|-动态X参数模型与FF结构相结合所获得的HLT1(|A0|,|Γ21|,Ω)、HLT2(|A0|,|Γ21|,Ω)两个参数在|Γ21|牵引下的LTM核函数。

3 模型提取和验证

提取LTM核函数的传统方法是采用双音信号激励模型进行提取，该方法采用不同的功率信号产生不同的电平，此法导致信号的谐波相位参考的最小频率分辨率固定在10 MHz，这远大于信号的频率间隔，以至于很难将两组信号的包络进行分隔。本文采用以窄带阶跃信号代替双音信号作为激励对核函数进行提取，窄带信号的周期远远短于长期记忆效应的持续时间，该方法没有额外的校准程序和硬件设备需要重建，因此被测器件的电流输出是过去几个输入信号周期的结果。使用窄带阶跃信号提取本文改进的X参数模型，入射波信号可以在t=0时刻发生转换：

(47)

窄带阶跃信号A(t)验证过程如图2，其中A0为当前输入，A1表示过去输入。

图2 窄带阶跃信号示意图Fig. 2 Schematic diagram of narrow band step signal

由图2可以看出，窄带信号类似于两个射频脉冲信号，其占空比为50%，周期时间是20 μs。此时的X参数模型为：

B(t)=FCW(|A(t)|,|Γ21|)P+

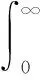
(48)

动态核函数为：

G(|A(t)|,|Γ21|Ω)=HST(|A(t)|,|Γ21|,Ω)·

(1+HLT(|A(t)|,|Γ21|,Ω))

(49)

本文提出的X参数模型中包含STM核函数和LTM核函数，参数|Γ21|提取问题可看作最小二乘法问题，采用随机相位法确定样本点后进行模型提取。将STM看作静态X参数的核函数，LTM看作X参数模型动态部分的核函数。使用安捷伦公司的ADS(Advanced Design System)软件提取静态X参数HST，使用脉冲测量获取H(·)，令负载反射系数|Γ21|的值为0.8，如图3所示，此时大信号的工作区域不再局限于一个特定的负载点，而是Smith圆图上的一个负载圆，通过对电路进行包络瞬态仿真和阶跃信号仿真，获得式(50)所需的系数：

Xp(|A11|,|Γ21|,Ω)=

(50)

其中X"P(|A11|,|Γ21|,∞)=X"P(|A11|,|Γ21|)，利用正交表分解法求解矩阵[20]使模型植入系统仿真，其过程为：通过提取的Xp(|A11|,|Γ21|,Ω)的系数，利用奇异值分解(Singular Value Decomposition， SVD)[20]来创建M个正交偏置矢量Ψxpyp,m(|A11|,|Γ21|)，最后利用最小二乘法来确定权值函数。权值函数代表线性滤波器的传递函数，可以使用时域矢量拟合的过程通过经典的极点/残基有效地合成，使卷积变成了简单的迭代算法，从而提高了建模的速度。正交基矢量Ψxpyp,m(|A11|,|Γ21|)利用三次样条曲线来代表。

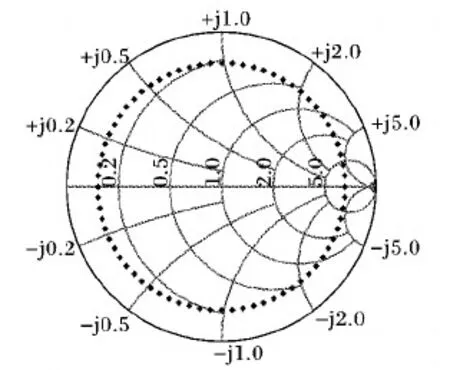
图3 |Γ21|=0.8时的负载反射系数圆Fig. 3 Load reflection coefficient circle when |Γ21|=0.8

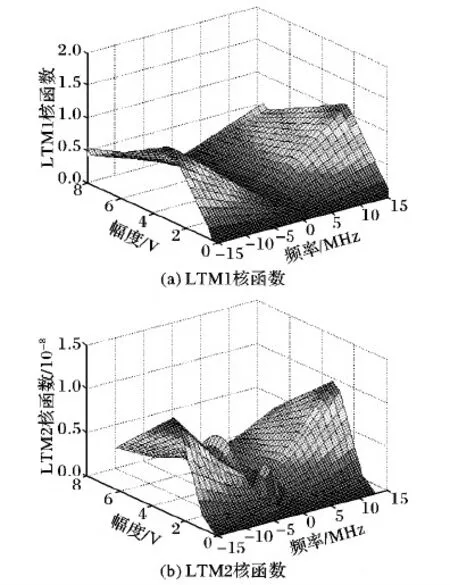
图4 LTM核函数提取结果Fig. 4 Extraction results of LTM kernel function

对于新的X参数模型，在理论上，如果一个模型含有m个参数则需要m次独立的测量，但是为减少误差，适当增加了测量的次数。对于X参数的3个参数，在功放整个带宽进行16次测量，选择30个频点，每个频点选取20个幅值，用以构建核函数，对STM内核和LTM内核进行提取后在Matlab中进行建模并仿真。通过瞬时包络仿真以及谐波平衡仿真获取功放输入和输出信号的包络及频率信息以提取LTM核函数，函数提取结果如图4所示。本文采用Gree公司的氮化镓(GaN)材料制作的CGH40045F晶体管设计一款功放，工作频段为0～4 GHz，静态工作点的漏极电压VDS=28 V，栅极电压VGS=-3 V，1 GHz时输入功率从0到45 dBm的功放增益—输入功率曲线如图5所示。本次测量利用ADS产生输入功率为32 dBm的信号，通过双向负载牵引匹配电路，设置负载反射系数|Γ21|=0.8，使用大信号激励功放模型，图6为测量输出端口各次谐波幅度值。由图6可得随着功放非线性增强，二次谐波及三次谐波的急剧上升，新模型能够很好地预测功放强非线性失真。

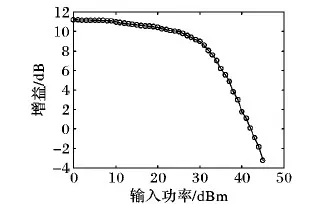
图5 功率为1 GHz时的功放增益Fig. 5 Power amplifier gain at power of 1 GHz

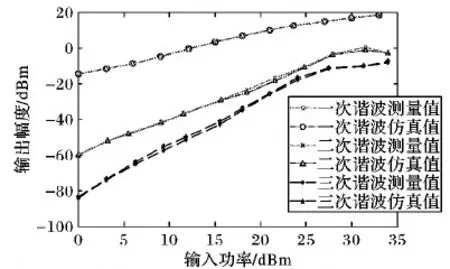
图6 功放输出谐波Fig. 6 Amplifier output harmonics

当射频功放工作在1 GHz时，此时放大器工作在强非线性情况，图7展示了输入信号在端口2处的幅值|A21|，在本文的测试情况下，入射波在端口2的幅度从1.6 V变化到6.65 V，仿真使用输出电压作为比较指标，本文模型与之前模型仿真获取输出电压与实测电压对比结果如图8所示。从图8可以看出，本文模型在该种非线性情况下与其他模型相比能够提供更好的预测效果。

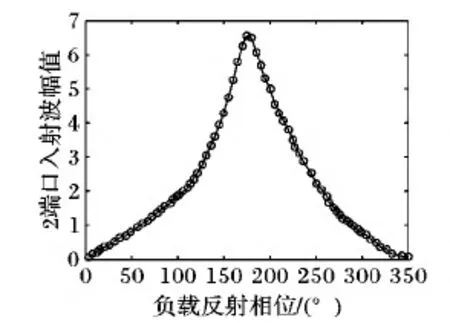
图7 端口2处反射波幅值Fig. 7 Reflection wave amplitude at port 2

通过提取不同负载反射相位时的输出电压以获得相对误差，相对误差为绝对误差与实测输出电压功率的比值，其中绝对误差为实测输出电压功率与使用模型提取输出电压功率的差值的绝对值，如图9所示，采用本文的建模方案进行仿真所产生的相对误差与使用传统的动态X参数模型进行建模的相对误差相比有明显降低，与之前改进的FF结构方案和FB结构方案相比更加精确。从图10的对比中可以看出，使用本文中的新型X参数模型来对功放建模，与其他三种模型相比能够更好地表征功率放大器在记忆效应下的特性，能够有效地预测功放在带外的频谱再生特性，仿真精度有所提高。同时通过由表1展示的模型仿真时间可以看出，本文模型通过负载反射幅值结合X参数模型和利用窄带阶跃信号提取X参数的新方法有效地提高了仿真效率，在保证精度和准确度的情况下，与FB结构X参数模型和FB结构X参数模型相比，仿真时间分别减少了1.64 s和4.08 s。

表1 模型仿真时间Tab. 1 Simulation time of model

图8 实测与四种建模方案输出电压的对比Fig. 8 Comparison between output voltage of four kinds of modeling program and actual measurement

图9 四种建模方案相对误差的对比Fig. 9 Relative error comparison of four kinds of modeling programs

4 结语

考虑功放记忆效应的特点和传统X参数模型易出现谐波失配的情况，本文在传统双记忆路径表征功放记忆效应的基础上结合负载反射系数，通过改进的FF结构并结合X参数进一步表征动态核函数，提出输入信号幅度与负载反射系数幅值及频率相关的核函数，建立具有记忆效应的非线性射频功放模型。利用窄带阶跃信号代替双音激励，采用ADS软件对模型进行提取，通过Matlab的仿真对比，本文的新型动态X参数模型建模方案能够对射频功放的非线性和记忆效应进行更加精确的表征。该模型为进一步研究系统级行为模型和谐波失配条件下建模提供了一种思路，但该模型仿真时需要获取较多数据集合易造成较大工作量，后续仍需进一步改进。

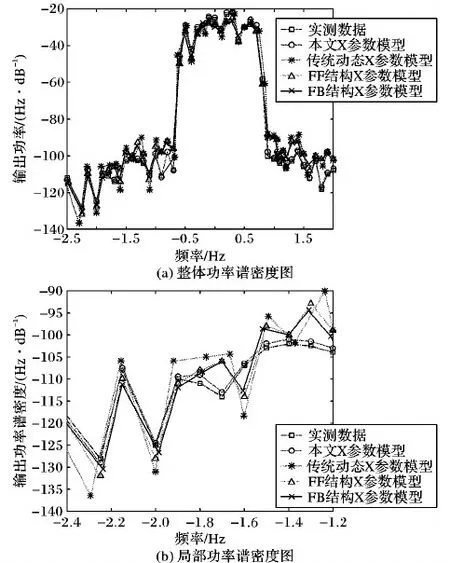
图10 实测与四种建模方案输出功率谱密度的对比Fig. 10 Comparison between output power spectral density of four kinds of modeling program and actual measurement