基于MapReduce的大数据主动学习
2018-11-22翟俊海张素芳刘晓萌
翟俊海,张素芳,王 聪,沈 矗,刘晓萌
(1.河北大学 数学与信息科学学院,河北 保定 071002; 2. 河北省机器学习与计算智能重点实验室(河北大学),河北 保定 071002; 3.中国气象局气象干部培训学院 河北分院,河北 保定 071002)(*通信作者电子邮箱mczsf@126.com)
0 引言
大数据具有以下几个特征[1-3]:海量(Volume)、多模态(Variety)、变化速度快(Velocity)、蕴含价值高(Value)和可靠性高(Veracity)。在大数据环境下,传统的机器学习面临着巨大的挑战,其中也包括主动学习[4-5]。主动学习算法大致可以分为两大类:基于池的主动学习算法和基于流的主动学习算法。
在基于池的主动学习研究中,主要集中在新的样例选取策略和应用研究上。Huang等[6]在文献中定义了样例代表性的概念,并将样例的信息量和代表性结合起来,提出了一种选择既富含信息量又具有代表性的无类标样例的算法,该方法受到了国内外同行的好评。在文献[6]的基础上,Du等[7]进一步研究了基于信息量和代表性的主动学习算法。传统的主动学习算法对已经进行标注的样例不再进行改变,Zhang等[8]针对这一问题,提出了一种双向主动学习算法,对已经进行标注的样例还可以删除,用这种方法选择出的样例具有更高的质量,用标注类标的样例训练出的分类器具有更强的泛化能力。在批处理模式的主动学习中,样例块的大小是固定的,Chakraborty等[9]提出了一种自适应的批处理主动学习算法,并用基于梯度下降的方法优化主动样例选择的策略。与固定块模式的主动学习算法相比,用该算法选择的样例更具代表性。基于排序的思想,Cardoso等[10]从另一个角度改进了批处理主动学习方法,提出了一种排序批处理主动学习算法,取得了很好的效果。而Long等[11]通过优化期望损失,提出了一种针对排序学习的主动学习算法,这两种主动学习算法有异曲同工之处。受集成学习中分类器多样性概念的启发,Gu等[12]定义了样例多样性的概念,提出了一种组合样例不确定性和多样性的主动学习算法,并应用于图像分类,取得了很好的效果。Wang等[13]将样例的多样性和信息量结合起来,提出了一种多示例主动学习算法。Du等[14]将主动学习推广到多标签学习的情况,提出了一种基于最大相关熵的多标签主动学习算法,并应用于图像标注,该方法扩展了主动学习的应用范畴,具有重要的理论及应用价值。Shen等[15]将分布式的处理机制引入到主动学习中,设计了分布式样本选择策略和分布式主动学习算法,并实验验证了算法的有效性。Lipor等[16]将主动样例选择的思想应用到信号处理中的空域信号选择,提出了一种基于距离惩罚的主动学习方法。
基于流的主动学习也可以看作基于池的主动学习的在线版本。这类方法早期代表性的工作包括:Cohn等[17]提出的方法和Dagan等[18]提出的方法。与基于池的主动学习相比,基于流的主动学习效率较低,因此研究相对较少。近几年,比较有代表性的工作包括:Smailovic等[19]针对金融领域数据语义分析,提出的一种基于流的主动学习算法;该算法用支持向量机作为分类器,用不确定性作为选择无类别样例的启发式。基于样例加权机制,Bouguelia等[20]提出的一种自适应流主动学习算法。
截至目前,无论是基于池的主动学习还是基于流的主动学习,研究人员提出的算法都是针对中小规模的主动学习问题。针对大规模主动学习问题的研究还很少,仅有Silva等[21]针对Twitter大数据提出了一种主动流形学习方法。然而,该方法是用流形学习方法进行降维,用基于支持向量机的主动学习方法减少有类标样例数据集的大小,严格地说还不是真正意义上的大数据主动学习[4,22-23]。
本文基于MapReduce[24]提出了一种大数据主动学习算法——MR-AL(MapReduce based Active Learning)算法。该算法以并行的方式在云计算平台上从无类别标签的大数据集中选择重要的样例,以信息熵作为无类别标签样例重要性的度量,以极限学习机(Extreme Learning Machine, ELM)作为分类器。
1 基础知识
1.1 主动学习
主动学习[4,22-23]可用一个四元组AL刻画,AL=(C,L,U,O)。其中,C表示分类器,L表示有类别标签的样例集合,U表示无类别标签的样例集合,O表示领域专家。主动学习是一个迭代学习的过程,如图1[23]所示。开始时,L包含少量有类别标签的样例;然后用某种训练算法从L中训练一个分类器C,并用某种预定义的度量指标评估U中样例的重要性,选择若干个重要的样例交给领域专家O进行标注;然后,将标注的样例添加到L中。重复这一过程若干次,直到训练出的分类器C具有好的泛化性能,主动学习过程结束。
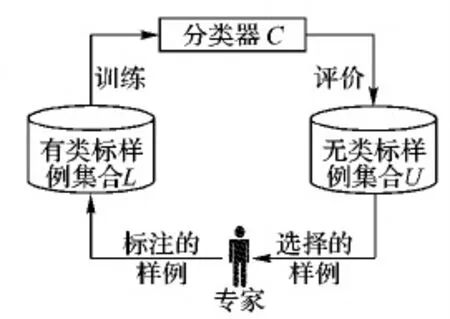
图1 主动学习过程示意图Fig. 1 Schematic diagram of active learning process
在主动学习中,不确定性是最常用的样例选择准则,这种准则分为三种[23]:
1)最小置信度准则。
这种准则用概率学习模型计算或估计样例的后验概率,用式(1)选择样例。
(1)

2)最大熵准则。
这种准则用信息熵度量样例的不确定性,用式(2)选择样例。
(2)
其中:yi表示样例的类标。
3)投票熵准则。
设C表示由若干个分类器构成的委员会,投票熵准则用式(3)选择样例。
(3)
其中:V(yi)表示类标yi获得的票数;|C|表示委员会C中包含的分类器个数。
1.2 MapReduce
MapReduce[24]是一种简单易用的软件编程框架,它采用“分而治之”的思想,把对大数据的处理分发到集群的各个节点上并行完成,接着通过整合各个节点的中间结果,得到最终的处理结果。从MapReduce的名字可以看出,MapReduce处理大数据的过程分为两个阶段:Map阶段和Reduce阶段。用MapReduce解决实际问题时,用户的应用逻辑由Map和Reduce两个函数来实现。换句话说,MapReduce处理大数据的思路是把大数据划分为相互独立的数据块,这些数据块以完全并行的方式由Map函数和Reduce函数处理。
Map函数的输入是一系列键值对,用〈K1,V1〉表示。其输出也是一系列键对,把每一个键以及与之关联的值组成一个列表,这一过程称为数据重排,重排的结果用〈K2,LIST(V2)〉表示。Reduce函数的输入是〈K2,LIST(V2)〉,其输出是另一系列键值对,用〈K3,V3〉表示。MapReduce的输入和输出以及中间结果均存储在HDFS(Hadoop Distributed File System)中。MapReduce对用户是透明的,许多底层细节系统自动完成,如数据的划分与分发、任务调度与监控、节点之间的负载均衡与通信、失败节点的检测与恢复等。用MapReduce处理数据的过程如图2所示。

图2 MapReduce处理数据的流程Fig. 2 Process of data processing with MapReduce
1.3 极限学习机
极限学习机(ELM)[25]是训练如图3所示的单隐含层前馈神经网络(Single hidden Layer Feed-forward Neural network, SLFN)的随机化算法。
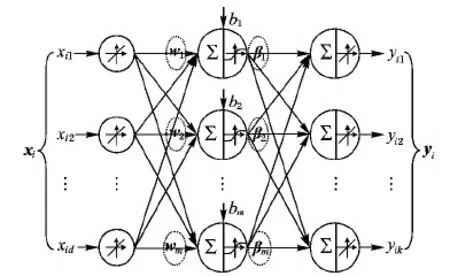
图3 单隐含层前馈神经网络Fig. 3 Feed-forward neural network with single hidden layer
给定训练集D={(xi,yi)|xi∈Rd,yi∈Rk}(1≤i≤n),图3所示SLFN的输入与输出之间是一种线性关系,可用式(4)表示:
(4)
其中:m是隐含层节点的个数;g是激活函数;wj是输入层节点到隐含层第j个节点的连接权;bj是隐含层第j个节点的偏置;βj是隐含层第j个节点到输出层节点的连接权。在式(4)中,wj和bj是用随机化方法按着某种概率分布(如均匀分布)给定的,ELM算法的随机性就体现在这里。而式(4)中的βj是唯一需要确定的参数,可用给定的训练集用最小二乘拟合来估计它。将训练集中的样例xi(1≤i≤n)逐个代入式(4)中,可得:
(5)
式(5)是由n个线性方程组成的线性方程组,它可以写成如下的矩阵形式:
Hβ=Y
(6)
其中:
H=
T表示转置;H是单隐含层前馈神经网络的隐含层输出矩阵,它的第j列是隐含层第j个节点相对于输入x1,x2,…,xn的输出,它的第i行是隐含层相对于输入xi的输出。如果单隐含层前馈神经网络的隐含层节点个数m等于样例的个数n,那么矩阵H是可逆的方阵。此时,用训练集得到的单隐含层前馈神经网络模型没有误差,即误差为零。但一般情况下,m≤n,即隐含层节点个数远远小于训练样例个数。此时,H不是一个方阵,方程(6)没有精确解。根据线性方程理论,可以通过求解优化问题(7)来得到方程(6)的近似解,这种近似解称为最小范数最小二乘解。

(7)
优化问题(7)的最小范数最小二乘解由式(8)给出:
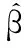
(8)
其中:H+是矩阵H的Moore-Penrose广义逆矩阵。
2 本文算法
大数据主动学习中的大数据是指无类别标签的数据集U是大数据集,而有类别标签的数据集L是中小型数据集。本文算法利用MapReduce的分治策略,将大数据集U划分为若干个子集,并部署到不同的云计算节点上,这些节点并行地选择重要的样例交给专家O进行标注。因为有类别标签的数据集L是中小型数据集,所以分类器L的训练是在本地进行的。本文MR-AL算法用极限学习机作为分类器,用式(2)给出的最大熵原则选择重要的样例。为了计算无类别标签样例的信息熵,需要对ELM的输出用式(9)的软最大化函数进行变换,使之成为一个后验概率分布。
(9)
用MapReduce实现大数据主动学习,关键是Map函数和Reduce函数的设计。在迭代学习的过程中,每次都要执行Map和Reduce操作,中间还有一个Shuffle操作,主要负责在各自的节点上对中间结果进行合并、排序。Map的输出是Reduce的输入,而所有的输入和输出都是以键值对的形式传输的。其中,涉及4个键值对,分别加以说明:〈k1,v1〉代表Map的输入,实际是从HDFS中获取数据,k1代表数据的偏移量,而v1是数据;〈k2,v2〉代表Map的输出,在MR-AL中,经过Map的处理,k2代表每个样例的信息熵的倒数,v2为样例;〈k3,v3〉代表Reduce的输入,即Map的输出,k2=k3,但v3是经过Shuffle操作得到的一个集合;〈k4,v4〉代表Reduce的输出,实际输出到HDFS中进行保存,k4在MR-AL中设计为空值Nullwritable,它代表利用信息熵准则选择出来的样例。以上是整个MapReduce的键值对设计。具体实现时,在Map阶段主要完成的功能包括:使用本地训练的ELM分类器对无类标的样例进行预测,对结果作软最大处理,之后计算信息熵,得到样例的信息熵后,就构成了需要的〈k2,v2〉键值对。Hadoop的Shuffle阶段会以k2,也就是信息熵进行排序,Reduce阶段功能相对简单,就是在排好序的数据中取出前q个样例,q为用户指定的参数,最终输出〈k4,v4〉,将选择的样例保存到HDFS中完成一次迭代。Map函数和Reduce函数的伪代码在算法1和2中给出。
算法1 MR-AL Map函数。
输入 〈k1,v1〉, 其中:k1为偏移量,v1为未标记样例。
输出 〈k2,v2〉, 其中:k2为样例信息熵的倒数,v2为标记后样例。
对数据进行预处理,包括数据分片,将分片数据变换为矩阵pre_matrix;
ELM.test(pre_matrix), 对数据进行预测, 得到predict_matrix;
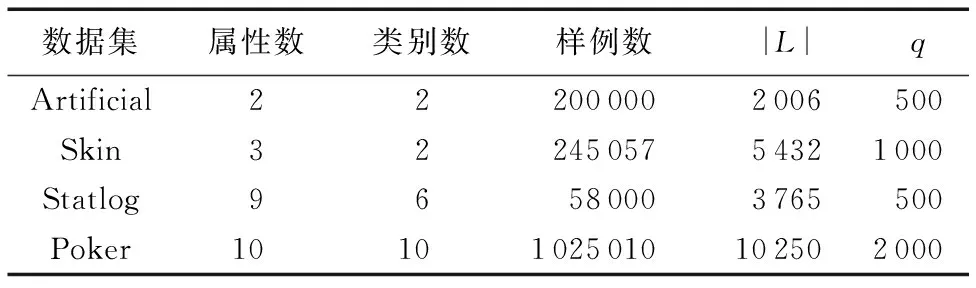
for(i=0;i 对predict_matrix进行软最大化处理; end for(i=0;i 计算样例的信息熵, 得到entropy; end context.write(new DoubleWritable(1/entropy), new Text(value)); 算法2 MR-AL Reduce函数。 输入 〈k2,v2〉, 其中:k2为熵倒数,v2为已标记样例。 输出 〈k3,v3〉, 其中:k3为Null值,v3为选择的样例。 if(q>0) then //q为用户指定的选择样例个数 for(test:v2) do context.write(Null值,text); //text为每个已标记样例 end end 图4 MR-AL方法在不同数据集上的实验结果对比Fig. 4 Comparison of experimental results on different data sets by MR-AL 为了验证本文算法的有效性,在4个数据集上与AL-ELM(Active Learning based on ELM)方法[26]进行了对比实验。4个数据集中包括1个人工数据集和3个UCI数据集。人工数据集(记为Artificial)是一个两类数据集,由高斯分布产生,两类服从的高斯分布参数列于表1中,所用数据集的基本信息如表2所示。在实验中,对于每一个数据集,随机选择一定数量的样例作为初始训练集L,初始训练集L包含的样例数列于表2的第5列。对于未选择的样例,隐去其类别信息作为无类别标签数据集U使用。 实验所用的Hadoop集群包括一个主节点和两个从节点,每个节点基本配置信息为:处理器Intel Core i5-2400 3.10 GHz,内存4 GB,硬盘10 GB,操作系统为64位ubuntu16.04。每个节点配置的软件环境如下: Java选用的开发包为jdk-1.8-linux-x64、Hadoop-2.7.3。 在4个数据集上进行了两个实验:一个实验用于发现标注的样例数与分类器测试精度之间的关系。对于不同的数据集,在迭代学习的过程中,每一次迭代,选择q个样例进行标注,并记录分类器的测试精度,实验结果如图4所示。另一个实验是在测试精度相同的前提下,与AL-ELM进行了运行时间的比较,实验结果如表3所示。从表3可以看出,本文算法在运行效率上远远优于AL-ELM算法,AL-ELM算法在3个数据集上没有得到运行结果,而本文算法都能得到运行结果,从而验证了本文算法的有效性。 表1 人工数据集的高斯分布参数Tab. 1 Parameters of Gaussian distribution for data set artificial 表2 实验所用数据集的基本信息Tab. 2 Basic information of data sets used in the experiments 表3 MR-AL与AL-ELM在运行时间上的比较 sTab. 3 Comparison of running time between MR-AL and AL-ELM s 利用Hadoop MapReduce自身具有的分治特性,提出了一种大数据主动学习算法——MR-AL。MR-AL算法以信息熵作为样例重要性的度量,利用极限学习机作为分类器。本文算法思想简单,易于实现,能有效地从无类别标签的大数据集中选择出重要的样例。与AL-ELM算法的对比实验结果表明,本文MR-AL算法在四个数据集上均能得到运行结果,而AL-ELM算法在三个大数据集Artificial、Skin和Poker无法得到结果。进一步的工作包括:1)在更多更大的数据集上进行实验,以进一步说明本文算法具有好的可扩展性;2)研究自适应地选择样例数是否可行;3)研究基于Spark的大数据主动学习,并用本文方法进行比较,分析两种方法在泛化能力和运行时间上有无本质区别。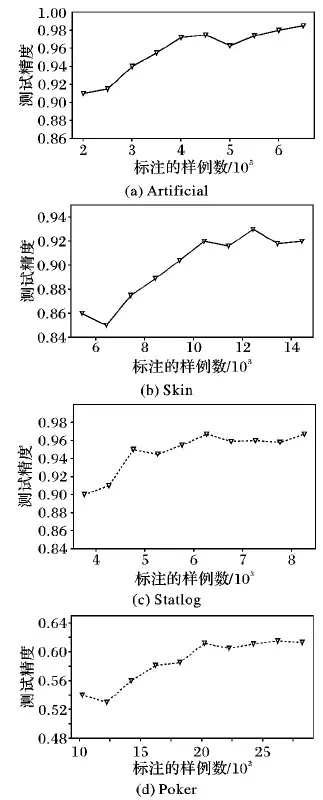
3 实验与分析


4 结语
