基于概率模型的非均匀数据聚类算法

杨天鹏，陈黎飞,2

(1.福建师范大学 数学与信息学院，福州 350117; 2.福建师范大学 数字福建环境监测物联网实验室，福州 350117)(*通信作者电子邮箱clfei@fjnu.edu.cn)

0 引言

聚类分析作为数据挖掘的一种重要方法，目的是将给定数据划分成多个子集(每个子集为一个簇)，使得簇内对象彼此相似，与其他簇对象不相似[1]。传统的聚类算法可分为层次聚类、基于划分聚类、基于密度和网格聚类，以及其他聚类算法[2-3]。目前聚类分析已广泛应用在Web搜索、图像处理、模式识别、医疗数据分析等众多领域。

作为数据挖掘十大算法之一，K-means算法[4]因其简单高效的优点得到广泛的研究和应用[5]。然而，受“均匀效应(uniform effect)”的影响[6]，K-means型算法在聚类医疗诊断等复杂数据时性能受限。这类数据的一个特点是同一数据集同时包含了样本数量和样本密度有较大差异的簇，这种数据称为非均匀数据(non-uniform data)。与不平衡数据(主要指簇样本量即簇大小差异较大的数据)聚类[7]相比，非均匀数据聚类问题更具普遍性。例如，在含有“正常”和“患病”两个簇的疾病诊断数据中，两簇的大小差异明显(通常，“正常”簇比“患病”簇的样本数量大得多)，更重要地，“患病”簇的样本皆具特定的疾病模式，其密度比“正常”簇有显著区别(表现为“正常”簇样本分布的方差大得多)。

针对该问题研究者提出了多种方法[8-12]，可大致分为三类：第一类方法基于样本抽样，在聚类之前首先对样本集作欠采样或过采样的处理操作，文献[8-9]即是在这样预处理后的数据上进行K-means聚类的；第二类方法在聚类模型中考虑不同簇的样本量差异，例如，文献[10]引入簇的样本数量，给出了经典模糊聚类算法目标优化函数的两种改进方案；第三类方法则侧重簇的密度差异，借助多代表点等方法[11]以区分数据集中的不同密度区域。这些方法是分别针对簇样本数量不平衡特性或密度差异特性而提出的，未提供同时处置非均匀数据上述两个特性的解决方案。

从原理上说，K-means型聚类是一种基于模型的方法，它所学习的概率模型是以相关参数为常数这一假设前提下的一种简化的高斯混合模型[13]，此简化模型并不能很好地刻画非均匀数据簇类的两个特点。为此，本文提出一种基于概率模型的非均匀数据聚类新算法——MCN(Model-based Clustering on Non-uniform data)，以应对传统K-means型算法的“均匀效应”问题。本文的主要工作包括两个方面：其一，以高斯混合模型为基础，建立了非均匀数据簇的概率模型，新模型可以描述同一数据集中样本量和密度都存在差异的簇；其二，基于提出的模型推导了聚类目标函数，并给出优化目标函数的算法步骤，实现了非均匀数据的软子空间聚类。在合成数据和实际数据上的实验结果表明，与现有的非均匀数据聚类算法相比，本文MCN算法有效提高了聚类精度。

1 相关工作

首先给出文中使用的符号及定义。令待聚类数据集为DB，含N个D维样本，任一样本用x=〈x1,x2,…,xj,…,xD〉表示，其第j(j=1,2,…,D)维属性为xj。考虑硬聚类算法，它将DB划分成K个不相交的子集的集合C={c1,c2,…,ck,…,cK}, 并称子集ck为DB的第k(k=1,2,…,K)个簇，|ck|表示该簇包含的样本数量。用vk=〈vk1,vk2,…,vkD〉表示ck的簇中心,V={v1,v2,…,vK}为全体簇中心的集合。

经典的K-means算法是一种划分型聚类算法，其优化目标定义为：

(1)

K-means通过类期望最大化(Expectation Maximization, EM)算法[15]的学习过程求取式(1)的局部优解，过程如下：给定簇数目K，首先选择K个初始簇中心，然后计算每个样本与各簇中心点的距离，将样本划分至距离最小的簇，再为每个新划分生成的簇计算最优的簇中心；算法迭代执行上述“划分-簇中心优化”步骤，直到满足停止条件算法终止，得到对应式(1)局部优解的数据集聚类划分。

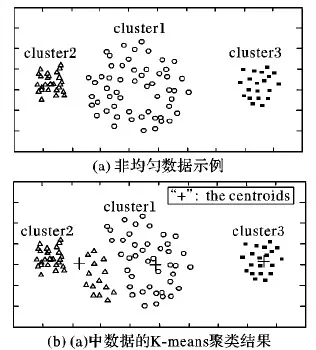
图1 “均匀效应”的例子Tab. 1 An example of “uniform effect”

文献[6]分析了K-means聚类的“均匀效应”现象。以聚类图1(a)中的非均匀数据为例。图1(a)隐含有3个簇Cluster1、Cluster2和Cluster3，它们不但在大小(样本数)上有差异，簇密度也显著不同，例如，Cluster1和Cluster2中样本分布方差显然有较大差别。该数据的K-means聚类结果如图1(b)所示，其中样本数较少的Cluster2会“吞掉”样本较多的簇Cluster1的部分样本，使得两个簇的大小和密度趋向于相同，此即K-means型算法的“均匀效应”。

从统计学习[16]的角度，K-means可以看作是一种基于模型的统计聚类算法。这里，视簇ck的每个样本x源自如下高斯分布：

(2)

那么，给定数据集DB，划分聚类的目标就是搜索最小化下面负对数似然函数的模型参数(C,V)：

(3)

注意到式(3)的推导结果与K-means算法的优化目标是相同的，见式(1)。

上面推导过程基于如下基本假设：每个簇的样本方差σ是一个常数。如前所述，σ体现了簇的密度。这从模型的角度解释了 “均匀效应”产生的一个原因：K-means型算法致力于求解密度相近的簇集合。此外，从式(3)还可以看出，K-means算法的优化目标也没有体现不同簇中样本数量的差异，这也是其所假设的概率模型所决定的：对应不同簇的高斯分布分量以一种“平等”的方式进行混合建模。因此，为提高K-means型算法在非均匀数据上的聚类性能，下面首先提出一种新的高斯混合模型，以区分簇类在样本数量和密度上的差异；接着，以此为基础，推导出一种新型的非均匀数据聚类算法。

2 非均匀数据聚类模型及算法

本章首先建立用于非均匀数据聚类的高斯混合模型，然后定义基于模型的聚类目标优化函数，最后给出聚类算法。

2.1 非均匀数据聚类模型

如前所述，在一个非均匀数据集中，簇的密度通常存在差异。为刻画这种差异，引入两组记号：用σk2(k=1,2,…,K)表示簇ck的方差，其值越大，表明ck的密度越小；进一步，引入向量wk=〈wk1,wk2,…,wkj,…,wkD〉，其各元素wkj>0，用于区分簇ck在不同属性上的密度差异，值越大表明ck投影在相应属性上时数据分布的密度越小。由此，ck属性j上数据分布的方差可用σk2/wkj来表示。将这个方差表达式代入形如式(2)的高斯密度函数，得到任意样本x∈ck投影在属性j上的概率密度函数，如下：

(4)

在此基础上，基于数据集的D个属性是统计独立的这一“朴素”假设[17]来建立簇的模型。虽然该假设在一些实际数据上并不现实，但它可以有效降低所构造模型的复杂性：简单地通过一组变量边缘分布的乘积来估计向量的概率密度。这样，令P(x)表示ck中任一样本的概率密度，有:

(5)

接下来，考虑非均匀数据的另一个特性：同一数据可能包含大小各异的簇。为此，引入代表簇大小的记号αk(k=1, 2,…,K)，满足约束条件：

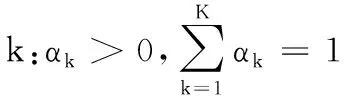
(6)

其数值大小与簇所包含的样本数量相关，可以看作是赋予每个簇的一种权重。根据这些定义，非均匀数据的加权似然函数表示为：

(7)

其中：Θ={(ck,σk,vk,wk)|k=1,2,…,K}为K组参数的集合。

基于上述模型，给定数据集DB和簇数K，聚类转变成了从DB求取优化的参数Θ以最大化加权似然的问题：

上式在式(7)基础上使用了对数变换，受条件式(6)约束。代入式(4)和(5)，并略去其中的常数项，优化目标改写为：

(8)

对比式(1)可知：

1)当所有的αk、σk和wkj都为常数，J2退化为K-means算法的优化目标函数J0。这意味着K-means假定了所有簇具有相同的大小和相同的方差，且各簇每个属性上的数据分布密度也是相同的。而新的目标函数通过σk、vk和wk等参数可以区分簇类这些各异的特性；

2)在J2表达式中，wkj主要作用于xj与vkj间距离(实际上是二者间的平方误差，数值上等于二者欧氏距离值的平方)的计算。从效果上看，衡量属性密度差异的wkj(j=1,2,…,D)相当于赋予各属性的特征权重，其数值大小反映了各属性对距离度量的贡献程度。因此，优化J2的过程可以看作是对非均匀数据集实施的软子空间聚类[14]。

2.2 软子空间聚类算法

根据拉格朗日乘子法，将wkj、αk的约束条件引入到目标函数中，可得带约束条件的聚类优化目标函数为：

(9)

其中：λk和η为拉格朗日乘子。

上述目标函数参数的求解是非线性函数的优化问题，难以求得全局最优解。本文MCN算法基于常用的EM算法结构求取其局部最优解。为叙述方便，引入符号W={wkj|k=1,2,…,K;j=1,2,…,D}和Λ={α1,α2,…,αK,σ1,σ2,…,σK}。参数的求解可分为以下几个步骤：

1)固定W、V、Λ,求C。对任意一个样本x根据以下公式进行簇划分：

(10)

式(10)通过比较样本x源自各高斯分量的概率将其划分到概率最大的簇中。

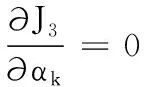
αk=|ck|/N

(11)

(12)

从式(12)可知，σk2即是第k个簇中样本分布的加权散度，反映了非均匀数据中各簇有差异的密度信息。根据以上分析，算法的最优解αk和σk2能刻画非均匀数据中不同簇之间样本数量和密度都可能存在差异的特点。

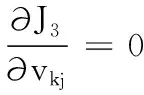
(13)

式(13)为簇中心点求解公式，通过该式完成簇中心点的更新。

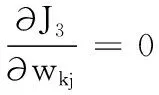
(14)

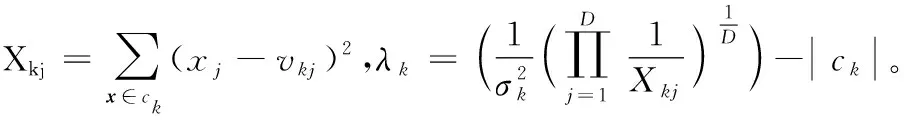
式(14)通过求解wkj为各特征赋予不同的权重，效果上相当于将第k个簇的样本投影到相应的子空间中。

根据上述参数求解方法，可以得到基于概率模型的非均匀数据软子空间聚类算法如下。

输入 数据集DB，簇数目K。

输出 簇划分C。

初始化 随机生成初始簇中心vk,并令wkj=1/D,σk=1/K,αk=1/K(k=1,2,…,K;j=1,2,…,D)。

Repeat:

更新C：利用式(10)更新簇划分；

更新vkj：根据式(13)，更新vkj；

更新αk、σk：根据式(11)、(12)更新αk、σk;

计算wkj：先计算λk,并将求得的λk代入到式(14)中求得wkj;

Until:满足迭代停止条件

根据上述算法步骤可知本文MCN算法的时间复杂度为O(PKND)，其中P为算法的迭代次数。

3 实验

实验平台为：Core i5-3470 3.2 GHz CPU，4 GB内存，操作系统为Windows 7。算法采用Java编写。

3.1 实验设置

实验选择了GMM[16]、Verify2[19]、IFCM[10]三种算法进行对比。GMM作为基于概率模型的典型聚类算法，将其作为对比算法用来验证经典的概率模型和结合子空间技术的概率模型在非均匀数据上的表现；Verify2为文献[19]提出的一种将欠采样和谱聚类结合对类不平衡数据进行聚类分析的方法，其中欠采样是非均匀数据预处理方法中的一种代表性方法；IFCM为文献[10]中提出的基于样本数量加权的模糊聚类算法。

图2 DS1投影到部分低维空间中的数据分布Tab. 2 Distribution of DS1 projected on some low-dimensional spaces

因为非均匀数据不同簇之间样本存在较大差异，合成数据能够从簇的数目、大小等控制数据集的簇结构，便于分析算法的性能及算法性能与簇结构之间的关系。首先在多个合成数据上进行测试，然后在4个真实数据上实验。由于各数据集已知类标签，选择两个外部评价指标Macro-F1[13]和标准化互信息(Normalized Mutual Information, NMI)[20]来评估各种算法的聚类性能，指标的值越大表明聚类效果越好。

其中：F1(classk)为第k个簇的F1值；P(classk,ci)和R(classk,ci)分别表示数据集中真实的类classk与聚类结果中簇ci相比的准确率和召回率；classk表示数据集中第k个真实的类;nk表示classk包含的样本点数。

NMI的计算公式如下：

其中：nij表示真实数据集中类i与聚类结果中簇j相一致的样本点数目;ni表示属于类i的样本点数目;nj表示属于簇j的样本点数目;R表示真实类别数，实验中设定K=R。

3.2 合成数据实验结果

实验中利用numpy中的random.multivariate_norma()函数合成三个数据集。由于二类数据可以直观表现簇结构，因此，在合成数据时，将簇数目固定为两类；此外，使用方差σ衡量各簇中样本的分布散度。合成数据的主要参数如表1所示。如表1所示，三个合成数据集的样本数量逐个递增，以此来验证本文MCN算法在不同数据量下的性能表现；同时，注意到同个数据集不同簇之间样本数量和样本方差都有较大差异。三个合成数据集的数据维度也逐个递增，以此测试不同数据维度下各算法的性能。

为直观地展现合成数据中样本的分布情况，将DS1投影到部分维度所确定的低维空间中，投影结果如图2所示。从图2可知，DS1中的多数类(样本数量较多的簇)的数据分布较为分散，少数类的分布则较为集中，且两个簇存在交叠现象。

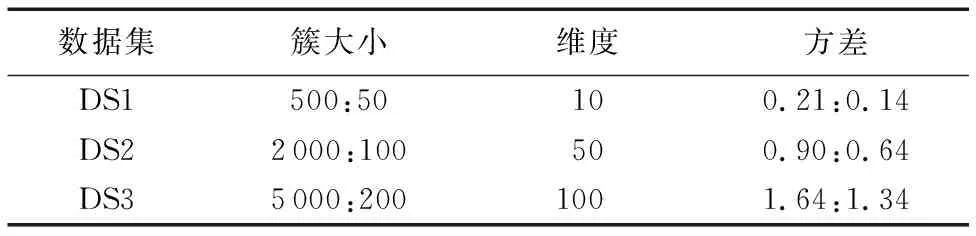
表1 合成数据集参数Tab. 1 Parameters of synthetic datasets

表2显示不同算法在合成数据集上取得的聚类结果。如表所示，本文MCN算法的聚类精度和NMI值都优于对比算法，表明MCN能更好地聚类此型非均匀数据。GMM算法在三个合成数据集上的NMI值均为0，这是因为GMM算法将数据中的所有样本都划分到同一个簇中，侧面反映了基于经典高斯模型的方法并不能有效处理非均匀数据。在两个指标上，IFCM算法与GMM接近。Verify2的聚类精度最低，但与GMM和IFCM算法相比，其NMI值有一定的提升，表明基于样本抽样的方法对非均匀数据聚类效果的改善有限。

表2 合成数据集不同算法聚类结果Tab. 2 Clustering results of different algorithms on synthetic datasets

不同算法在合成数据上的运行时间如表3所示。表3中，本文MCN算法的运行时间低于对比算法GMM、Verify2和IFCM。Verify2的运行时间远高于GMM和MCN算法，一个主要原因是Verify2采用了谱聚类方法，涉及到矩阵特征值计算等，当样本数量和数据维度较大时，其算法运行时间较长。

表3 不同算法在合成数据上的运行时间 sTab. 3 Running time of different algorithms on synthetic datasets s

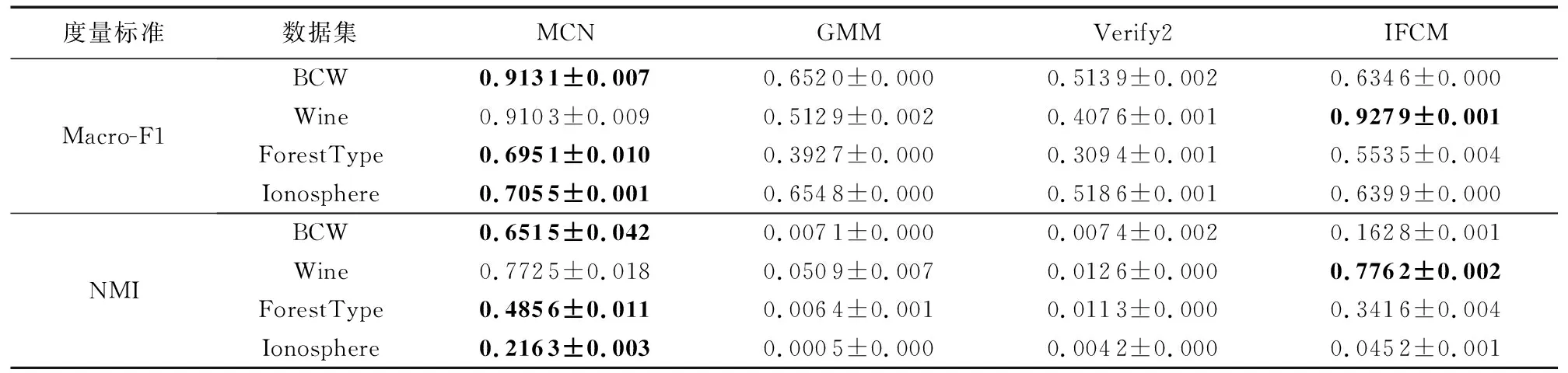
表5 算法在实际数据集上的聚类结果Tab. 5 Clustering results of different algorithms on real-world datasets

3.3 实际数据实验结果

实验使用的实际数据来自聚类分析常用的UCI Machine Learning Repository(http://Archive.ics.uci.edu/ml/datasets.html)。选用了四个实际数据集：Breast Cancer Wisconsin(简写为BCW)、Wine、 ForestType和Ionosphere，数据集主要参数如表4所示。其中，BCW为乳腺癌诊断数据，包含241个恶性样本和458个良性样本；Wine是相关研究常用的不平衡数据集，其普通品质酒类的样本数较多，而品质较好和品质较差的样本数量则较少；ForestType是森林遥感数据，包含三种不同的森林类型和一类空地，其中Sugi forest类的样本数量较多；Ionosphere为电离层雷达波数据，其中具有某种特定结构的样本数量较多。这四个数据集中，不同簇类的样本数有较大差异，且样本分布(方差)也存在差异，是典型的非均匀数据。实验将基于BCW、 Wine数据集验证各种算法在低维数据上的性能，在ForestType、Ionosphere上对比算法在较高维度数据上的表现。本文MCN算法与对比算法在四个实际数据上的聚类结果如表5所示。表5显示，MCN算法在Wine数据上的两项指标稍低于IFCM算法，但在其他数据集上的聚类精度和NMI值都明显优于对比算法，表明MCN算法可以有效聚类实际应用中的非均匀数据。

表4 实际数据集参数Tab. 4 Parameters of real-world datasets

如前所述，本文提出的MCN算法可以实现非均匀数据的子空间聚类,实现途径是在聚类过程中自动地赋予每个特征以不同的权重。下面以Wine数据集为例，从MCN算法的一次聚类结果中提取特征权重信息，作进一步分析。图3显示该数据集中三个簇(分别记为Cluster1、Cluster2和Cluster3)各自的13个特征(分别命名为A1,A2,…,A13)的权重分布。

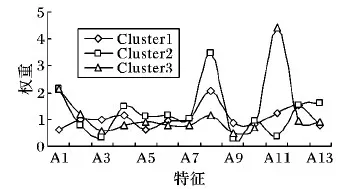
图3 Wine数据中三个簇的特征权重分布Fig. 3 Distribution of feature weights of three clusters in dataset Wine

如图3所示，不同簇的特征权重分布并不相同。例如，对于Cluster3，MCN算法赋予A11(指“酒的色调”)较大的权重，这表明“色调”对识别Cluster3有重要的作用；而特征A8(一种称为“Nonflavanoid phenols”的酚类化学物质)对Cluster2中酒的品质有较大影响。以上结果表明，MCN算法可以有效识别特征对于不同簇类有差别的贡献度，从而提高了实际应用中非均匀数据聚类的性能。

4 结语

针对K-means型算法的“均匀效应”问题，本文提出了MCN算法。首先分析了经典K-means算法隐含使用的概率模型，它是基于有关参数为常数这一假设的高斯混合模型，此简化模型并不能很好地刻画非均匀数据簇之间样本数量和密度都有较大差异的特点。接着，从概率模型角度入手，结合软子空间聚类技术定义了一种非均匀数据簇的概率模型，并推导出了相应的聚类优化目标函数。最后给出了MCN的算法过程。在合成数据和实际数据上的实验结果表明，与GMM、Verify2、IFCM等算法相比，MCN算法在多数情况下都可以取得较大的聚类性能提升，从而验证了本文所提算法的有效性。

在大数据时代如何结合大数据处理工具分析非均匀数据是一项有意义的工作，因此下一步将结合分布式Spark平台进一步研究非均匀数据聚类新方法。