基于引力模型的多标签分类算法
2018-11-22李兆玉王纪超
李兆玉,王纪超,雷 曼,龚 琴
(重庆邮电大学 通信与信息工程学院,重庆 400065)(*通信作者电子邮箱576233728@qq.com)
0 引言
传统的监督分类是机器学习领域中的一个重要组成部分,它的研究目的是将一条数据划分到预先定义好的某一个类别当中。若预先定义好的类别只有一个,这样的分类问题被称为单标签分类或二值分类。若存在多个类别,将数据划分到其中之一,这样的分类问题被称为多类分类。多标签分类是当前的研究热点之一,并被广泛应用于文本分类[1]、图像标注[2]、蛋白质功能分析[3]等多个方面。
多标签分类问题的形式化定义如下:
定义1 已知一个定义在实数域R上的d维特征空间,记作F;一个q维的标签空间,记作L;包含m个训练数据的训练集合D。
D={(Xi,Yi)|1≤i≤m,Xi⊆F,Yi⊆L}
(1)
其中:Xi={xi1,xi2,…,xid}和Yi={yi1,yi2,…,yiq}分别为样本i的特征部分和标签部分。则多标签分类可以描述为:通过对训练集D的学习,获得分类模型f:F→L,该模型能够为待测数据Xt预测一个标签集合Yt。
多标签分类算法解决问题的思路可以概括为以下两种:问题转化方法和算法适应方法[4]。问题转化方法是指将多标签问题转化为多个独立的单标签问题,利用单标签分类器对每一个标签进行预测,如二元关联(Binary Relevance, BR)方法[5]、标签幂集(Label Powerset, LP)方法[6]等。BR方法按照标签个数,将多标签数据集分割为q个单标签数据集,然后采用单标签方法进行分类。BR方法假设标签间是相互独立的,忽略了标签间的相关性,浪费了多标签数据的标签信息。LP方法利用可能的标签组合,将多标签数据集分割为多个单标签数据集,然后采用单标签方法进行分类,但这样往往造成了较高的复杂度。
算法适应方法是将单标签算法进行改进,使单标签算法能够处理多标签问题。典型的算法适应方法有ML-kNN(Multi-Labelk-Nearst Neibors)方法[7]、BPMLL(BP-Multi-Label Learning)方法[8]等。ML-kNN方法根据待测样本k个近邻的标签信息对每个标签采用最大后验准则进行预测。BPMLL方法将BP神经网络扩展为多个输出,依据误差度量函数对标签进行排序获得预测值。ML-kNN和BPMLL算法均没有考虑标签间的相关性,造成了标签信息的浪费。
综上所述,本文采用算法适应方法,对现有算法进行改进,提出了一种基于引力模型的多标签分类算法,简称MLBGM。算法继承了引力模型简洁、易理解的特点并且考虑了标签的相关性。关于标签相关性,不仅考虑了标签同时出现时代表的正相关关系,同时也发掘了标签互斥所代表的负相关关系,充分利用了标签间的相关关系。通过在不同数据集上进行的对比实验结果表明,该算法在性能上优于对比算法。
1 相关工作
1.1 引力模型
引力模型因其形式简单且效果良好被广泛应用于信息处理及国际贸易等领域。文献[9]首次将引力模型用于聚类分析并与非引力方式的聚类方法进行了对比,结果表明引入引力模型后的方法取得了较好的结果。文献[10]介绍了一种考虑引力坍缩的kNN分类器的改进算法,但该算法将所有数据粒子的质量设为一个统一的定值,一定程度上忽略了数据间的差异性。根据数据引力和引力场理论,Yang等[11]提出了一种基于数据引力的分类器(Data Gravitation Classifier, DGC)并将其用于入侵检测系统(Intrusion Detection System, IDS)。该方法通过计算数据质心将多个数据组成的数据簇进行粒化,然而不平衡数据将严重影响质心的计算,降低分类效果。基于DGC算法,Peng等[12]提出一种通过缩放引力系数来处理不平衡数据的改进算法IDGC(Imbalanced Data Gravitation Classifier),但IDGC算法并不适用于多标签数据。Reyes等[13]对经典引力计算公式进行修改,提出了一种适用于多标签数据的分类算法MLDGC(Multi-Label Data Gravitation Classifier)。该算法将每个样本作为一个数据粒子,单独计算每个粒子对待测样本的引力来完成分类任务。但MLDGC没有考虑标签相关性,会造成标签信息的丢失。本文提出的MLBGM对引力模型进行了改进,优化了相互作用系数,并充分利用了标签间不同的相关性。通过对比实验结果表明,MLBGM在性能上优于对比算法。
数据引力的计算由经典力学中万有引力公式演变而来。原始引力模型计算粒子i、j间引力的方法可表示如下:
(2)
用于多标签数据的数据引力定义如下。
定义2 粒子i与其近邻集合中粒子j之间的引力为:
(3)
将式(2)中质量与引力系数的乘积定义为相互作用系数,记作Cj。数据粒子i与数据粒子j之间的引力与Cj成正比与dF(i,j)成反比。
1.2 标签相关性
在多标签分类中,一个样本可以同时拥有多个标签,并且这些标签往往具有相关性。例如,一张图片(如图1)拥有标签“蓝天”。而标签“蓝天”与标签“白云”有很强的相关性,利用标签相关性有利于提高正确识别图片中的“白云”的概率。这种标签与标签之间倾向于同时出现的关系通常称为标签间的正相关。

图1 有“蓝天”标签的图片Fig. 1 Picture with label “Blue Sky”
以往多标签分类研究在考虑标签相关性时,多采用计算标签间正相关关系的方式来提升分类性能[14-16],然而标签之间往往还存在着互斥现象。例如,一张图片拥有标签“大海”,那么它将很有可能拥有标签“轮船”,而拥有标签“火车”的可能性则会很低(如图2)。这种标签间的排斥现象是相互的,这种互斥关系可以称为标签间的负相关关系。
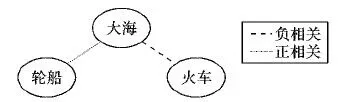
图2 标签正、负相关性示意图Fig. 2 Label positive and negative correlations
多标签数据拥有不止一个类别标签,因此含有丰富的标签信息,利用标签信息能够提升分类效果。通过挖掘标签间不同的相关关系对多标签数据的标签信息进行充分利用。
2 基于引力模型的多标签分类算法
基于引力模型的多标签分类算法首先将每一个样本数据作为一个数据粒子,然后利用形式简单的数据引力计算公式来计算粒子间的相互作用。最后,对待测样本其近邻集合的引力求和,构造分类函数。该算法形式简单,在不过度增加算法复杂度的条件下,同时考虑了标签间正、负相关性,有效利用了多标签数据的标签信息。
2.1 近邻密度与近邻权重
距离计算采用异构重叠欧氏度量(Heterogeneous Euclidean-Overlap Metric, HEOM),该度量方法不仅能够处理数值型数据,还能够处理标称型数据[17]。根据HEOM的计算方法,样本i与样本j之间的距离为:
(4)
当数据为离散型数据时:
(5)
当数据为连续型数据时:
(6)
其中:F为特征空间;xif代表样本i的第f个特征;max(f)、min(f)分别为最大、最小的特征值。
根据异构重叠欧氏度量方法计算样本i与训练集中其他样本的距离,将距离依照大小进行升序(降序)排序,选取距离最小的k个样本作为样本i的近邻集合,记作δ(i)。
然后,应用引力模型将样本数据转化为数据粒子的形式。将每一个样本数据都转化为一个数据粒子,根据物理中常见的形式对数据粒子进行定义,则样本i可以转化为数据粒子i,记作(Xi,Yi,Ci)。其中:Ci为相互作用系数,Ci越大,样本i与其他样本之间的引力越大。Ci由近邻密度di和近邻权重wi组成,计算公式如下:
Ci=diwi
(7)
近邻密度di表示粒子i的近邻粒子的分布情况,di的值越大,则Ni中与粒子i标签相似度高的粒子距离粒子i的距离越近。di的计算方式如下:
(8)
其中:dL(i,j)=|YiΔYj|/q,代表了粒子i与粒子j标签部分的差异的大小;Δ表示求两个集合的对称差;q为标签部分长度。
近邻权重wi表示粒子i的近邻粒子对分类结果的贡献程度。由于多标签数据标签间的相关性对分类结果会产生影响,因此本文考虑了标签间不同的相关关系并将相关性作为近邻权重的一部分,则粒子i的近邻粒子对粒子i第l个标签的分类结果贡献程度计算如下:
(9)
其中:Pil和Nil分别为粒子i的第l个标签与其他标签之间的正、负相关性系数;ui表示近邻样本标签一致性的大小。
ui=pi(Fsim|Lsim)-pi(Fsim|Ldis)=
(10)
先验概率pi(Ldis)、pi(Fdis)、pi(Fdis|Fdis)计算方法如下:
(11)
(12)
(13)
2.2 分类器的构建
通过上述分析,根据式(3)可以计算近邻样本与样本i之间的引力。现给出测试样本i并为其预测第l个标签,则分类函数为:
(14)
基于引力模型的多标签分类算法在构造分类函数时采用了计算引力合力的方式,这里只计算力的数值大小,不考虑方向。则如果预测标签yil为1时,合力为:
(15)
同理,如果标签yil为0时,合力为:
(16)
由式(14)可知,当f+(i)>f-(i)时,yil=1;否则,yil=0。
2.3 算法描述
基于引力模型的多标签分类算法可以分为两个阶段:
1)训练阶段。通过对训练集数据的学习,获得标签间的相关性及引力计算所需的各种参数。采用基于近邻的方式,避免求取相关性时对整个数据集的计算。在提升分类效果的同时,不过多地增加算法的复杂度。
2)测试阶段。采用了形式简单的数据引力的计算方法,且参数计算在训练阶段都已完成,所以测试阶段具有较低的复杂度。
2.3.1 训练阶段
算法1 获取正、负相关矩阵及引力计算参数。
输入D为训练集;k为近邻个数。
输出P为正相关矩阵;N为负相关矩阵;di为近邻密度;ui为近邻一致性系数。
初始化P、N矩阵;
fori=1 tom:
获取样本i的近邻集合δ(i);
//式(4)
计算di、ui;
//式(8)、式(10)
foryij=1,1≤j≤q:
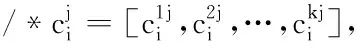
cpij=0,cnij=0;
foryil=1,1≤l≤q:
ifj≠landp(j=1|l=1,Ni)>Pr:
cpij=cpij+1;
Pij=cpij/q;
foryil=1,1≤l≤q:
ifj≠landp(j=1|l=0,Ni)>1-Pr:
cnij=cnij+1;
Nij=cnij/q;
获得正相关矩阵P和负相关矩阵N;
2.3.2 测试阶段
算法2 对测试样本进行标签预测。
输入t为测试样本;k为近邻个数;P为正相关矩阵;N为负相关矩阵;di为近邻密度;ui为近邻一致性系数。
输出Yt为预测出的测试样本的标签向量。
获取测试样本的近邻集合δ(i);
forl=1 toq:
分别计算f+(t)、f-(t);
//式(15)、式(16)
iff+(t)>f-(t):
yil=1;
else:
yil=0;
Yt={yt1,yt2,…,ytq};
3 实验与分析
3.1 实验设置
本文实验基于一个针对多标签学习的Java库Mulan(http://mulan.sourceforge.net/)来实现对比算法。通过与不同算法的实验结果进行对比,验证本文算法的有效性。所有算法均在7个不同的多标签数据集(见表1)上进行十折交叉验证。
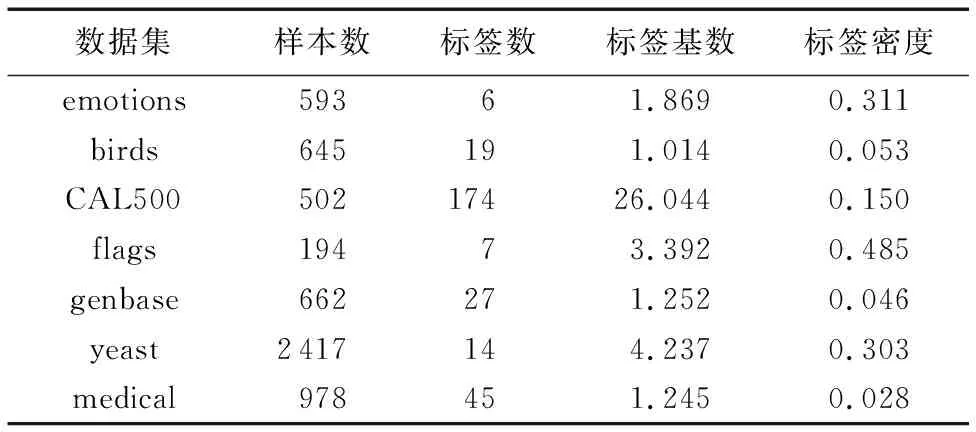
表1 实验中使用的多标签数据集Tab. 1 Multi-label dataset used in experiments

表2 不同算法的指标对比结果Tab. 2 Comparison of indicators of different algorithms
3.2 评价指标
由于单标签分类的结果是单一标签的预测值,而多标签分类的结果为一个预测标签集合,因此,原始单标签的评价指标并不完全适用于多标签分类。本文采用了汉明损失HammingLoss、微平均F1值MicroF1和子集准确率SubsetAccuracy来衡量分类效果。其中:HammingLoss和SubsetAccuracy是基于样本(example-based)的评价指标;MicroF1是基于标签(label-based)的评价指标。基于样本的评价指标通过分别评价每个样本的分类效果,然后返回整体的评价结果;基于标签的评价标准则是对每个标签的分类效果进行评价,返回宏/微平均结果。3种评价指标计算方法如下:
(17)

(18)
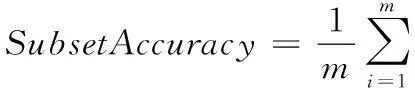
(19)

3.3 实验分析
将本文提出的MLBGM算法与MLkNN[7]、RAkEL[18]、HMC[19]、IBIR_ML[20]、BRkNN[21]这5个多标签分类算法在3个评价指标上进行对比,结果如表2所示,其中k值为每种算法在不同数据集上的最佳近邻数。
HammingLoss衡量了样本标签预测错误的比例[22],从对比结果可以看出:MLBGM的HammingLoss相对更小,说明MLBGM对样本标签错误预测的比例更低。
MicroF1值是对单标签评价指标F1值的扩展,F1值是对精确率(precision)与召回率(recall)的综合考虑。更高的MicroF1值一般表示更好的分类效果,因此在该指标上的对比结果中,MLBGM同样具有较好的效果。
SubsetAccuracy表示算法预测的标签与真实标签完全一致的样本数占标签总数的比例。SubsetAccuracy越大,则标签完全预测正确的可能性越大。从对比结果可以看出:MLBGM算法在HammingLoss、MicroF1、SubsetAccuracy三个指标上均优于对比算法。
实验采用了7个不同的数据集与5个现有的多标签分类算法在3个指标上进行了对比。实验结果显示,MLBGM与5种未考虑标签负相关的对比算法相比,HammingLoss平均降低了15.62%,MicroF1平均提升了7.12%,SubsetAccurary平均提升了14.88%。MLBGM在大多数数据集的指标上都存在明显优势,主要原因为MLkNN、RAkEL、HMC、BRkNN均没有考虑标签间的相关性,而IBLR_ML只考虑了标签间的正相关关系,没有考虑标签互斥,没有充分利用多标签数据的标签信息。综上,MLBGM算法在基于样本和基于标签的评价指标上均取得了较好的结果,验证了本文算法的有效性并且性能优于对比算法。
4 结语
本文提出了一种基于引力模型的多标签分类算法MLBGM。MLBGM充分利用了多标签数据标签间的相关性,能够有效地对多标签数据进行分类。算法运用物理学经典的引力模型并深入挖掘标签间正、负两种不同的相关性。在多个数据集上的对比实验结果表明,本文算法能够有效处理多标签数据的分类问题并且分类效果优于对比算法。后续研究将考虑标签数量及标签密度等因素对分类结果的影响,进一步提高算法性能。
