基于多维网格空间的改进K-means聚类算法

邵 伦,周新志,赵成萍,张 旭

(四川大学 电子信息学院,成都 610065)(*通信作者电子邮箱xz.zhou@scu.edu.cn)

0 引言

聚类算法是一种典型的无监督学习算法,是利用样本的特征比较样本的相似性,将具有相似属性的样本划分到同一类或簇中的算法[1-5]。聚类算法的应用广泛,在数据挖掘、信息检索和图像分割等方面都有重要的作用[6-11]。迄今为止已经衍生出了众多的聚类算法,这些算法可以分为划分法、层次法、密度法、图论法、网格法和模型法等[5,11-14]。K-means是一种典型的基于划分的聚类算法[12,16-17],其应用非常普遍,但是传统的K-means算法存在一些不足之处,比如随机选择的初始聚类中心通常是不理想的,易使最后的聚类结果局部最优,而非全局最优;另外初始聚类中心选择的不稳定性,也会导致算法迭代次数及聚类结果的不稳定[18-19]。很多研究人员对初始聚类中心的选择提出了优化的方法,文献[11]中提出了一种基于最小生成树的层次K-means聚类算法,文献[20]中提出了一种基于最小方差优化初始聚类中心的K-means算法,但是这些算法在初始聚类中心选择的效果上仍不够理想,聚类结果的稳定性和准确性仍有待提高。

针对上述问题,本文提出了一种基于多维网格空间结构优化初始聚类中心的改进K-means聚类算法。此算法首先根据样本集的属性个数n,将样本集映射到一个包含有限个子网格的n维网格空间结构中。其映射流程如下:以样本集中每一类属性的最大值和最小值作为网格空间中每一维度的上边界和下边界；接着，根据样本的类别数k,依次将每一维度均等切分成k等份;然后，计算出每个子网格中的样本数,选择包含样本数最多且距离较远的k个子网格作为初始聚类中心网格,再计算初始聚类中心网格中样本的均值点作为初始聚类中心;最后，依据距离作为相似性的评价标准来迭代更新聚类中心,直到找出最终的聚类中心。相对于传统的K-means算法中随机选择初始聚类中心的方法,本文算法基于多维网格空间目的性选择的初始聚类中心与实际聚类中心接近,使得算法的迭代次数明显减少,聚类结果稳定且错误率较低。

1 多维网格空间的设计

需要进行聚类分析的数据集其数据量往往较大,并且数据属性往往有多个,在这一大堆数据中随机选择初始聚类中心,通常很难选中与实际聚类中心相近的样本点作为初始聚类中心。设想将数据集映射到一个多维的网格空间中,由于数据样本各属性值的差异,数据集就被分散到了多个小的子网格之中,那么数据集便以空间化的形式得到粒化。另外,由于数据集中包含多个不同类别的样本,而不同类别的样本间属性值差异一般较大,因而分布在各个子网格中的样本数必定会存在差异,而且在同一子网格中的样本必定是距离相近的样本,即同一子网格中的样本很有可能属于同一类别。由此,有理由认为含样本数最多且距离较远的子网格是包含有实际聚类中心或者与实际聚类中心接近的网格,那么在此子网格中选定初始聚类中心便是与实际聚类中心最接近的,此子网格亦被称为初始聚类中心网格。

基于多维网格空间选择初始聚类中心网格,其网格空间中子网格的个数对于选择出完美的初始聚类中心网格至关重要:过多的子网格会使对样本集的切分过度细化,出现较多包含样本点个数无差异的子网格,对初始聚类中心网格的选择产生干扰;过少的子网格又无法将样本集中的所有类别完全切分开,出现一个子网格中包含较多多个类别的样本,导致最终无法正确选择初始聚类中心网格。如果按照数据集的类别数k来切分数据集,即将数据集所映射的多维空间结构中每一维度均等切分为k份,则所得子网格数最为合理,切分好后多维网格空间的子网格数为kn(n为数据集的属性个数)。

1.1 二维网格空间

假设如图1所示的样本集为X={X(1),X(2), …,X(m)},包含m个样本,共3类数据(即k=3),其中X(i)=(x(i),y(i))为单个样本,并且包含x(i)和y(i)(i∈{1, 2, …,m})两个属性特征。那么将样本集X映射到二维网格空间中,其每一维度均等切分3份,则切分后该二维网格空间包含9个同等形状和大小的子网格,如图2所示。其中，(x0,y0)小于或等于样本集中最小的点,(x3,y3)大于或等于样本集中最大的点,即：

∀i∈{1,2,…,m},有

(1)

(2)

令属性特征x(i)所代表的维度的切分步长为dx,属性特征y(i)所代表的维度的切分步长为dy,有

dx=(xmax-xmin)/3

(3)

dy=(ymax-ymin)/3

(4)

易知,xi=xi-1+dx和yi=yi-1+dy,其中i∈{1, 2, 3}。

为了方便标记二维网格空间中的子网格和记录每个子网格中样本点的个数,以(x0,x1;y0,y1)表示图2中左边下方的子网格,在此表示形式中,x0和y0分别称之为此子网格第1维度上和第2维度上的前界,x1和y1分别称之为此子网格第1维度上和第2维度上的后界,将此子网格中的样本点数记为w1;以(x0,x1;y1,y2)表示图2中左边中间的子网格,并将此子网格中的样本点数记为w2;依照此法,最后(x2,x3;y2,y3)表示图2中右边上方的子网格,并将此子网格中的样本点数记为w9。最终,可以得到样本集X映射到二维网格空间后各个子网格中样本点个数的分布为{w1,w2, …,w9},如图2所示,虚线框所标出的子网格(x0,x1;y2,y3)、(x1,x2;y0,y1)、(x2,x3;y2,y3)中的样本点数分别为w3、w4、w9。可以看出这3个子网格中样本数最多并且它们的距离较远,故样本集X的3个初始聚类中心网格就选择这3个子网格。

图1 二维属性数据集Fig. 1 Data set with two-dimensional attribute feature

图2 基于二维网格空间选择初始聚类中心网格Fig. 2 Initial cluster center grid selection based on two-dimensional grid space

1.2 三维网格空间

三维网格空间的设计及数学描述与二维网格空间基本一致。假设如图3所示的样本集为X={X(1),X(2), …,X(m)},包含m个样本,共3类数据,其中X(i)=(x(i),y(i),z(i))为单个样本,并且包含3个属性特征x(i)、y(i)和z(i),i∈{1, 2, …,m}。那么将样本集X映射到三维网格空间中,如图4所示,该三维网格空间包含27个同等形状和大小的子网格。其中,(x0,y0,z0)小于或等于样本集中最小的点,(x3,y3,z3)大于或等于样本集中最大的点,即

∀i∈{1,2,…,m},有

(5)

(6)

令属性特征x(i)所代表的维度的切分步长为dx,属性特征y(i)所代表的维度的切分步长为dy,属性特征z(i)所代表的维度的切分步长为dz，有

dx=(xmax-xmin)/3

(7)

dy=(ymax-ymin)/3

(8)

dz=(zmax-zmin)/3

(9)

易知,xi=xi-1+dx、yi=yi-1+dy和zi=zi-1+dz,其中i∈{1, 2, 3}。

同样,为了方便标记三维网格空间中的子网格和记录每个子网格中样本点的个数,以(x0,x1;y0,y1;z0,z1)、(x0,x1;y0,y1;z1,z2)、…、(x2,x3;y2,y3;z2,z3)表示各个子网格,并且各个子网格中样本点个数的分布为{w1,w2, …,w27}。如图4所示,粗虚线框所标出的子网格(x0,x1;y2,y3;z1,z2)、(x1,x2;y0,y1;z0,z1)和(x2,x3;y0,y1;z2,z3)中的样本点数分别为w8、w10、w21,可以看出这3个子网格中样本数最多并且它们的距离较远,故样本集X选择这3个子网格作为初始聚类中心网格。

图3 三维属性数据集Fig. 3 Data set with three dimensional attribute feature

图4 基于三维网格空间选择初始聚类中心网格Fig. 4 Initial cluster center grid selection based on three-dimensional grid space

1.3 n维网格空间

∀i∈{1,2,…,m},有

(10)

其中:j∈{1, 2, …,n}。

dj=(xj_max-xj_min)/k

(11)

其中:j∈{1, 2, …,n}。

记(x1_min,x1_min+d1;x2_min,x2_min+d2; …;xn_min,xn_min+dn)、 (x1_min,x1_min+d1;x2_min,x2_min+d2; …;xn_min,xn_min+2dn)、 …、 (x1_min+(ε-1)d1,x1_min+εd1;x2_min+(ε-1)d2,x2_min+εd2; …;xn_min+(ε-1)dn,xn_min+εdn)、 …、 (x1_min+(k-1)d1,x1_max;x2_min+(k-1)d2,x2_max; …;xn_min+(k-1)dn,xn_max)是各个子网格的表示形式,分号将子网格每一维度的前界和后界隔开,前界和后界又以逗号隔开,其中ε∈{1, 2, …,k},并且各个子网格中样本点个数的分布为{w1,w2, …,wkn}。

在选择初始聚类中心网格时,要考虑到的一个重要指标是各初始聚类中心网格之间的距离要比较远,下面给出此指标的判断公式:

令两个子网格之间的距离为D,有

(12)

或

(13)

若D满足式(14),则认为这两个子网格之间的距离较远。

∀j∈{1,2,…,n},有

D≥(k/2)×max{dj}

(14)

2 K-means算法的改进

本文对传统K-means算法的改进主要在于对初始聚类中心的选择方式作出了良好的改进,传统K-means算法是通过随机的方式选择出k个初始聚类中心,而本文算法是基于多维网格空间结构选择出k个初始聚类中心,多维网格空间以子网格的形式将数据集中属性相似的样本包裹、属性差异较大的样本隔离,此方法选择出来的初始聚类中心摆脱了随机性,并且基本接近实际的聚类中心。

算法具体流程:

1)输入包含m个样本的数据集X={X1,X2, …,Xm},其中每一个样本Xi为n维向量,其中n为样本属性个数,i∈{1, 2, …,m}。

2)初始化样本类别k,将数据集映射到虚拟的n维网格空间结构中。

详细步骤:首先,找到第1个属性的最大值和最小值,根据式(11)计算出步长,按照该步长将数据集分成k份;然后,再找到第2个属性的最大值和最小值,计算出步长,按照该步长将上一步分得的k份中的每一份再分成k份;依次递推,直到将数据集分成kn份,即完成将数据集映射到n维网格空间结构中了。

3)根据上一步构造网格空间结构的递进规则,依次计算每一个子网格中样本点的个数,得到{w1,w2, …,wkn}。

4)选择k个包含样本数最多,且两两之间距离D满足式(14)的初始聚类中心网格{G1,G2, …,Gk},再在各初始聚类中心网格中计算出其内含样本点的均值点,得到k个初始聚类中心{C1,C2, …,Ck},即：

其中:q∈{1,2,…,k};|Xi∈Gq|表示Gq所包含样本的个数。

5)依据K-means算法迭代步骤,更新聚类中心,直到最终聚类中心不再改变便停止迭代。

计算每个样本与每个初始聚类中心之间的相似度,将样本划分到最相似的类别中,即,若Xi与Cq之间欧氏距离d(Xi,Cq)最小,则Xi属于类别Cq。

计算划分到每个类别中的所有样本特征的均值,并将各均值作为各类新的聚类中心,重复步骤5)直到最终的聚类中心不再改变或达到最大迭代次数时停止更新聚类中心,即新的聚类中心有：

6)输出最终的聚类中心,以及每个样本所属的类别。

本文算法主要由两部分组成:第一部分是选择初始聚类中心,时间主要花费在将数据集映射到多维网格空间上,这部分的时间复杂度为O(knm)；第二部分是根据初始聚类中心来迭代更新聚类中心，这部分的时间复杂度与传统K-Means算法的时间复杂度一样为O(tknm)。两部分的时间复杂度相加即为本文算法的时间复杂度,所以本文算法的时间复杂度为O(tknm)；另外,空间复杂度为O((k+m)×n),其中：t表示迭代次数,k表示样本集类别个数,n表示样本属性个数,m表示样本数。

3 实验结果与分析

为了充分验证本文算法的效果,实验分为两个阶段:第一阶段采用计算机模拟的二维数据集作为实验数据,对传统的K-means算法和本文的基于多维网格空间的改进K-means算法进行可视化对比;第二阶段采用三个UCI数据集作为实验数据,分别对传统K-means算法、文献[11]算法、文献[20]算法和本文算法进行对比。实验环境是Windows 10操作系统,Intel Core i7-8550U处理器,8 GB内存,Python编程语言。

3.1 模拟数据集测试实验

计算机模拟的数据集具有4个类别,包含80个二维数据,如图5所示。通过此数据集分别对K-means算法和本文提出的改进算法进行聚类实验,各经过60次重复实验后,在实验结果中各随机挑选三组,如图6所示是K-means算法得到的三组实验结果。图7所示是本文的改进算法得到的三组实验结果,其中十字点为初始聚类中心,星形点为最终的聚类中心。对比这三组实验结果可以看出，K-means算法的初始聚类中心选择的随机性导致了迭代次数和聚类结果的不稳定,其中图6(b)所示的聚类结果B陷入了局部最优,与实际聚类中心的偏离非常大;而本文的改进算法的初始聚类中心非常稳定且与实际聚类中心距离较近,故算法迭代次数较少,最终的聚类结果准确和稳定。

图5 模拟的二维数据集Fig. 5 Simulated two-dimensional data set

3.2 UCI数据集测试实验

表1 UCI数据集描述Tab. 1 UCI data set description

三个UCI数据集Iris、Wine和Seeds的描述如表1所示。利用这三个数据集分别对传统K-means算法、文献[11]算法、文献[20]算法和本文算法进行了40次重复实验,记录每一次的迭代次数和错误率,实验结果如表2所示。从表2中四种算法的迭代次数可以看出，K-means算法的最大迭代次数基本都是最小迭代次数的4倍左右,迭代次数的不稳定是较为突出的问题;而本文算法的迭代次数是稳定不变的,非常接近K-means算法的最小迭代次数且略小于文献[11]和文献[20]算法的迭代次数。实验结果表明基于多维网格空间选择初始聚类中心对算法的收敛速度有较为明显的提升。

表2 4种算法在不同数据集上的实验结果Tab. 2 Experimental results of four algorithms on different data sets

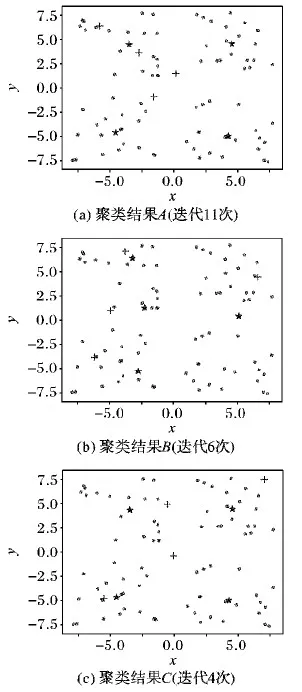
图6 K-means算法随机抽取的三组实验结果Fig. 6 Three groups of randomly selected experimental results of K-means algorithm

再对比四种算法的错误率,可以发现K-means算法的最大错误率一般是最小错误率的2到3倍;而本文算法的错误率稳定不变,并且都低于K-means、文献[11]和文献[20]算法的平均错误率。

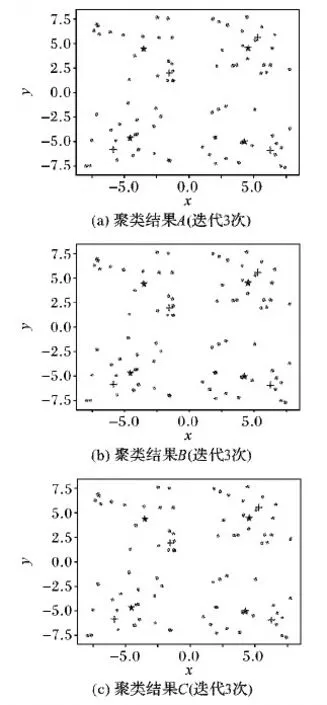
图7 改进的K-means算法随机抽取的三组实验结果Fig. 7 Three groups of randomly selected experimental results of the improved K-means algorithm

4 结语

本文提出的基于多维网格空间优化的K-means算法,其核心是通过多维网格空间分解数据集,凸显同类别数据之间的凝聚性和不同类别数据之间的距离差,从而选择出与实际聚类中心较为接近的初始聚类中心,克服了传统K-means算法易陷入局部最优，算法迭代次数和聚类结果不稳定的缺点。本文算法的聚类结果仍然依赖于距离作为相似性的度量方式,在接下来的工作中,将重点研究相似性的度量方式,在距离的基础上再综合考虑密度和属性间的相关系数等,探求从单一的相似性度量方式转变为综合的相似性度量方式,以实现更低错误率的聚类结果。