立足教材 活用教材
——“一元二次方程”教学设计及立意阐释
2018-11-19江苏省建湖县建阳中学谭万祝
☉江苏省建湖县建阳中学 谭万祝
近期,笔者有幸参加了所在地区初中数学“一人一课”活动,并取得了优异成绩.执教课题是“一元二次方程”.下面对其教学设计进行简单介绍,并给出一些初步思考,不当之处,敬请指正.
一、教学内容
第1页至第4页.
二、教学流程
1.知识回顾,情境引入

在复习一元一次方程相关知识的基础上,呈现教材第1页章前图、章引言及第2页问题1,并引导学生在明晰题意的基础上列出方程.
2.观察思考,得出定义
章前图、章引言 问题1
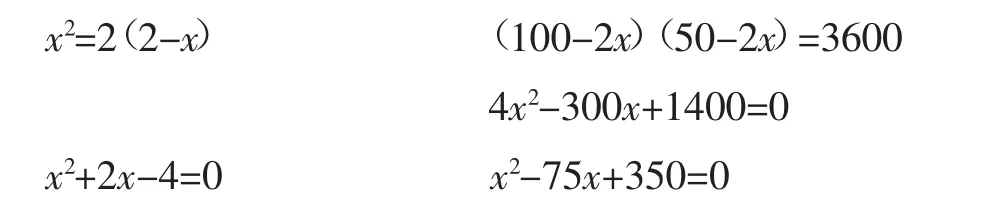
思考:(1)它们是一元一次方程吗?
(2)类比一元一次方程,你能给它们命名吗?能说出它们的主要特点吗?

图2
3.自主练习,微课助学
练习1:(1)你能举出一个一元二次方程的例子吗?
(2)你能举出一个不是一元二次方程的例子吗?为什么?
练习2:判断下列各方程是不是一元二次方程.如果不是,请说明理由.
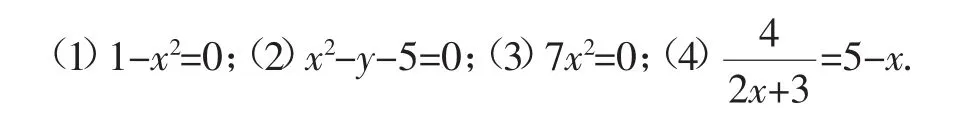
在完成练习1和练习2的基础上,播放微课:“一元二次方程”自述(PPT及微课文本如下所示).

图3
同学们,大家好,我叫“一元二次方程”,是你们这节课刚刚认识的新朋友,你们可能和我还不太熟悉,但我相信你们肯定和我的孪生兄弟“一元一次方程”是好朋友,它的样子如下:ax+b=0,其中a≠0,我们把ax称为一次项,a叫作一次项的系数,b称为常数项,比如3x-2=0的一次项是3x,一次项系数和常数项分别为3和-2.
我的样子如下:ax2+bx+c=0,其中a≠0,我们把ax2称为二次项,bx称为一次项,a、b分别叫作二次项和一次项的系数,而c称为常数项,比如3x2-2x-1=0的二次项、一次项、常数项分别为3x2、-2x、-1,而二次项系数和一次项系数分别为3和-2.
同学们,以后的日子我们慢慢相处吧,相信我们一定也会成为好朋友的.
4.巩固新知,典例分析

图4
典例分析:
呈现教材第3页例题.
练习3:将下列方程化为一元二次方程的一般形式,并写出其中的二次项系数、一次项系数和常数项.

练习4:教材第2页问题2.
呈现教材第2页问题2,并得到方程:x2-x=56,然后列表(如表1):

表1
通过亲自动手填写表1,很容易发现:当x=8时,x2-x=56;也很容易“唤醒”学生以前对方程的“根”的认识,进而可以很容易得到一元二次方程的“根”的概念.通过验证,我们发现:当x=-7时,x2-x=56也成立,这说明如果不考虑实际问题,x=-7也是方程x2-x=56的一个根.
此时出示本节课的学习目标:
(1)理解一元一次方程的概念是以未知数的个数和次数为标准的;
(2)掌握一元二次方程的一般形式及三种特殊形式,能将一元二次方程化成一般形式;
(3)理解一元二次方程根的概念,会判断一个数是否是一个一元二次方程的根.
5.达标检测,作业设计
达标检测:(1)下列方程是关于x的一元二次方程的是____(填序号).

(2)将关于x的一元二次方程(x+1)(x-3)=2(x-1)2化成一般形式,并指出二次项系数、一次项系数和常数项.
(3)m为方程x2+x-6=0的一个根,则代数式m2+m的值等于______.
作业设计:
必做题:(1)P4复习巩固1、2、3;(2)每人写一篇数学日记《一元二次方程自述》.
选做题:P4复习巩固6、7.
三、教学立意
1.贯彻“基本套路”
人民教育出版社资深编审章建跃博士曾指出:课堂教学要重视“基本套路”的教学.笔者认为,关于方程教学的“基本套路”就是:实际问题、定义(一般形式、根)、解方程、应用.因此,在本节课的教学之初,笔者就以框图的形式为学生呈现了一元一次方程的基本框架,在教学过程中渐次生成了一元二次方程的基本框架,为学生构建前后连贯、逻辑一致的知识体系进行了一定的尝试,且取得了较好的教学效果.
2.践行“用教材教”
笔者听过多次这节课的公开课,其中有很多教师直接类比一元一次方程的概念得到一元二次方程的概念,然后进行大量的练习,正所谓“一个定义+三项注意”,评课环节有的老师还说这是“用教材教”,关于这一点笔者持反对意见.上述做法其实违背了教材的编写意图,没有实现和教材的真正“对话”.现行人教版教材涉及方程(包括函数)等章节的内容都是以大量实际问题的形式引入新课,这样做一是为了引导学生体会数学来源于生活,二是为了将学生“列方程解决实际问题”的难点分解到每一个课时中去,而不是集中呈现,显然一开始提到的做法与这种理念是背道而驰的.因此,笔者在教学中直接应用了教材章前图(章引言)和问题1,并对问题2进行加工得到了一元二次方程根的概念,实现了课堂教学的预期效果.
