城市空间形态离散度指数NDIS构建与应用
2018-11-15贾玉秋唐立娜桂柳鸣
贾玉秋,唐立娜,桂柳鸣
1 中国科学院城市环境研究所城市环境与健康重点实验室,厦门 361021 2 中国科学院大学,北京 100049 3 中国科学院上海分院,上海 200031
2016年,我国城镇常住人口比重为57.35%,户籍人口城镇化率为41.2%(国家统计局)。未来很长的一段时间内,中国仍会持续推进城市化。但是,在城市化的历史过程中,无序扩张造成大多数城市的建设用地投入产出效率下降,甚至超过50%的城市有过多的建设用地投入,土地资源并未集约利用[1]。刘纪远等研究中国的土地利用发现,2000—2010年建设用地占用耕地占原有耕地减少面积的55.44%[2]。城市对其周边区域的生态胁迫日趋严重,所产生的一系列环境效应在区域乃至全球中的角色和贡献越来越受到重视[3- 4]。为了守住中国的耕地红线和粮食安全、对已开发土地实现高效利用、保护城市生态系统,中国城市形态仍然需要向更为紧凑的方向发展[5]。据紧凑城市理论,城市形态的紧凑不仅体现在城市内部高密度和土地利用的强混合,城市的空间布局也应该是紧凑的,也就是说城市总体形状越趋圆,城市资源配置越是节约,城市运行效率越高,甚至能够减少二氧化碳的排放水平[6- 9]。
城市空间紧凑性评价常用的指数有Richardson紧凑度[10]、Cole紧凑度指数[11]、Gibbs紧凑度指数[12]、Boyce-Clark形状指数[13]等刻画城市趋圆性的形态指数。同时,分形维数(FRAC)、分离度指数(SPLIT)、相似邻接百分比(PLADJ)、连续度指数(CONTIG)等形状类景观格局指数也常被用来衡量城市要素在空间上的连通和邻接程度[14- 17]。这些指数对城市形态的描述依赖面积、周长、半径等几何关系[18],其数理统计结果通常侧重表示城市形态的数量关系。中国已有很多城市开展了空间形态紧凑度的计算,形态指数一方面直接用来判断城市的紧凑水平,另一方面作为城市紧凑综合评价指标体系的一部分[19- 20]。紧凑度指数与人口密度、交通、用地混合性、生态环境等城市微观要素建立的关联还不够明确、清晰[21]。因此,从紧凑度和离散度两个方面分开刻画城市空间形态的紧凑性,更有利于对城市空间形态进行全面认识。
标准化紧凑度指数(Normalized Compactness Index, NCI)基于引力模型测算城市用地的紧凑度,是一个成熟有效的紧凑度指数,已有研究证明NCI与通勤时间密切相关[6]。Jaeger等提出的城市离散度指数DIS(Degree of urban dispersion)与NCI的共同点是非常重视城市斑块间的距离关系,并且DIS已成功运用到瑞士城市扩张的驱动力研究当中[22]。然而,DIS值在反映城市形态紧凑程度方面具有一些局限,因而,如何改进DIS,使其能够跟NCI结合,更全面地刻画城市空间形态的紧凑性,是本文将要研究的问题。
1 标准化离散度指数
1.1 离散度指数DIS
城市景观结构中建筑密度、高度的非均质对景观的度量造成了很大的难度,尤其是用来量化城市蔓延的指标,要能够表现出蔓延的方向、强度和属性就要采用最能代表和简化扩张过程的参数,而景观斑块的距离就是一个必不可少的因素。Jaeger提出的离散度指数DIS(Degree of urban dispersion)是在局部或区域范围内通过计算像元点间的加权距离衡量建设用地的离散性[23](图1,半径为R)。像元间的距离越远,对DIS值的贡献越大,城市景观就越离散。在满足对新增斑块的敏感性、数学公式的可读性和单调性等一系列标准之下,最简化的DIS计算见公式(1):
(1)
式中,i、j为邻域半径为R的圆形范围内任意两个像元;d(i,j)为像元i到j的欧几里得距离;ni为邻域半径内的像元个数;n为城市建设用地所有像元数;C是指邻域半径内仅有单个像元的DIS值,是保证公式有效的常数,对于30m分辨率的像元,C值为4.50。
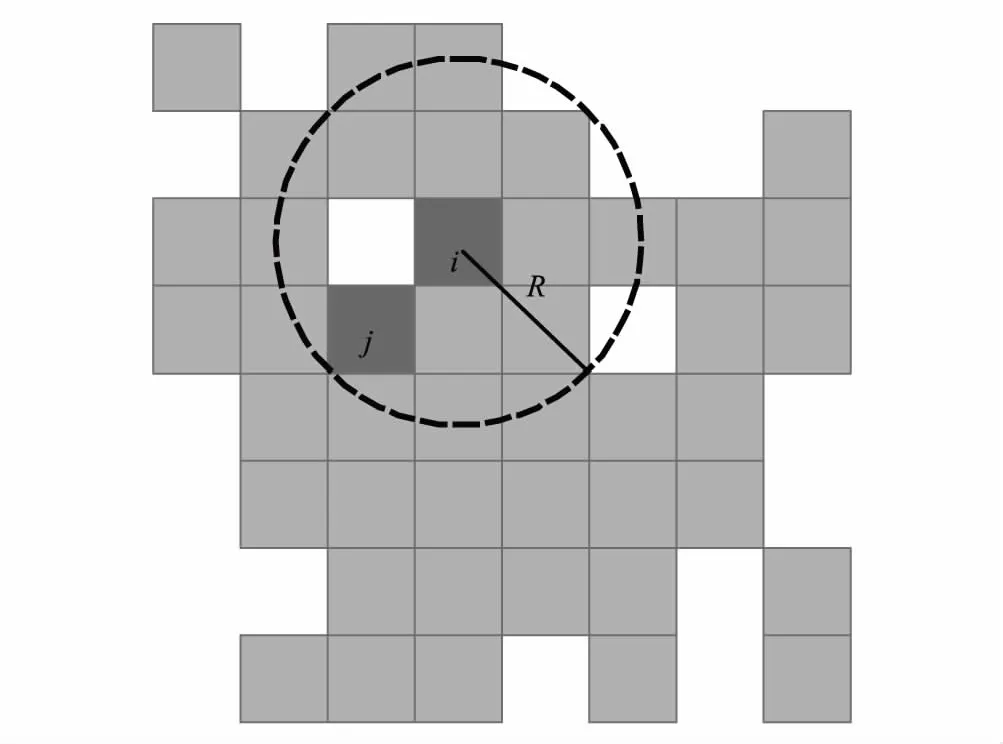
图1 DIS指标计算过程示意图Fig.1 Schematic diagram of calculation of DIS 灰色小方格代表建设用地像元30m×30 m,圆形框代表半径为R的邻域范围;DIS:离散度指数,Degree of urban dispersion;R:领域半径,Radius
1.2 离散度指数的标准化
DIS模型通过对加权距离的平均减弱了零碎斑块的影响,能够准确反映城市用地的总体离散性,具有广泛使用的价值。为了测试DIS对建设用地离散程度的响应能力,我们假设了图2中6种情境,包括具有相同形状但面积不等的图2a、2b、2c,面积与图2b相等但形状差异较大的图2d、2e、2f。在一个30m像元邻域半径范围内,DIS值具有如下特征:(1)方形面积越大,离散程度越高。(2)面积相同的图形中,方形(图2b)的离散程度最高,最为复杂的分散图形(图2d)的离散程度最低。这两个结论与事实相悖,并不能反映图形的真实离散程度。进一步对DIS的邻域半径进行调整发现(图3):(1)所有图形的DIS值都会随着邻域半径的增大而上升,直到在不同的节点达到稳定。(2)邻域半径较小时,部分图形的DIS值近似相等,在稳定状态的唯一值增加了图形间的可比性。图3中在DIS稳定状态,相同面积的图形中,离散程度从低到高依次为图2b、2f、2e、2d。因此,DIS值衡量建设用地的离散程度首先要克服值相近的问题,应采用稳定状态下的最大邻域半径进行计算。其次,相同图形离散程度应该是一致的,不应受到面积规模的干扰。研究借鉴NCI标准化过程,假设城市的紧凑建设是标准的圆形,实际建设用地的DIS值与同等面积圆形的DIS的比值便能够消除城市规模的影响(公式(2))。
(2)
式中,DISmax代表城市建设用地最大邻域半径下的DIS值,DIScircle-max表示最大邻域半径下同等面积圆形的DIS值。标准化的NDIS通常大于1,NDIS越大,城市偏离圆形的程度越大,建设用地分布就越离散;反之,NDIS值越接近于1,城市布局就越紧凑。在图2中,方形的NDIS接近于1,最紧凑;其次是长条形,NDIS=1.07;再次是多中心图形,NDIS=1.32;图2d布局最为离散,NDIS=1.35。

图2 面积相当、形状相同等图形下的DIS(30m邻域半径)及NDIS值Fig.2 DIS and NDIS value (30m neighborhood radius) of graphs with the same area or shapeDIS:离散度指数,Degree of urban dispersion;NDIS:标准化离散度指数,Normalized dispersion index
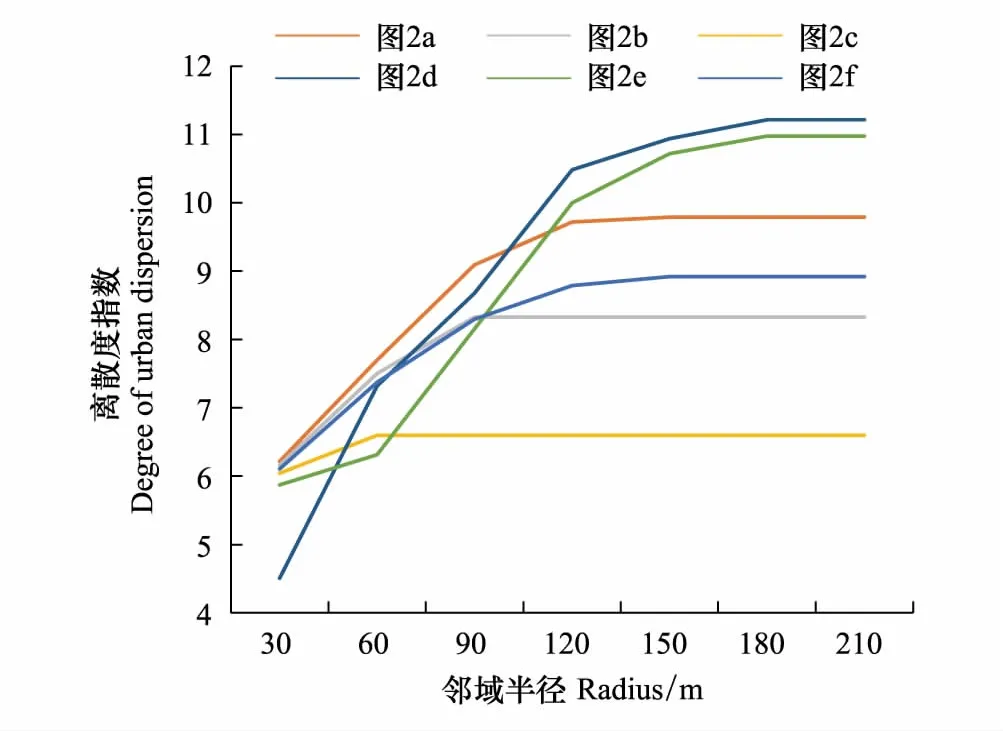
图3 6种图形的DIS对邻域半径变化的响应 Fig.3 The response of DIS of 6 graphs to neighborhood radius variation
2 案例分析
2.1 案例城市
本文选择4座直辖市、25座省会城市(不包括拉萨)、5座计划单列市共35座城市分别计算NDIS及NCI。NCI值的计算是作为NDIS的参照,确定二者的统计学意义和实际应用当中的区别与联系,其计算公式可详见赵景柱等[24]文献。中国发展速度最快的这35座城市,其所处的自然条件不同、发展策略不同,城市空间形态丰富多样。既有地处广阔平原的团块状城市;山间河谷平原发展的条带状城市;交通导向形成的放射状城市;也有城市发展到一定的规模形成的主城+卫星城的多中心组团结构等等,能够满足多种情境下对指数有效性的验证。其中,平原城市18座,山地城市8座,沿海城市9座。
2.2 城市建设用地提取
本文利用遥感手段提取城市建设用地(即不透水面),依据中国生态区选择Landsat 8 OLI最佳时相的影像[25],在相应时间区间内35个城市的Landsat 8 OLI无云影像共40景在地理空间数据云(http://www.gscloud.cn/)平台获取。以2015年为基年,部分城市缺少2015年的无云影像,采用相近的2014、2016年影像代替。首先,所有影像均进行辐射定标、大气校正、市辖区矢量边界裁剪。其次,采用高反射率不透水面、低反射率不透水面、植被和土壤四端元进行混合像元分解,据不透水面像元百分比结合归一化水体指数(MNDWI)进行像元尺度的分类,分类结果包括植被、土壤、建设用地和水体4个类别。最后,将栅格分类结果转化为矢量,提取建设用地图层对照Google earth进行人机交互修正,对错误斑块进行去除,遗漏的建设用地进行补充。准确的建设用地矢量结果最终转化为栅格数据用于紧凑度指标的计算。
2.3 NDIS与标准化紧凑度指数NCI比较
对于35座城市样本总体而言,NDIS最大值是兰州市的1.64,最小值是石家庄市的1.14,均值1.29±0.12(SE)。NCI最大值是郑州市0.39,最小值是宁波市的0.1,均值0.24±0.07(SE)。山地城市、沿海城市、平原城市的NDIS均值依次为1.35、1.34、1.24,NCI均值依次为0.25、0.22、0.25。通过NDIS的箱线图可知,三类城市的NDIS数值分布差异显著,层次分明。山地城市的NDIS值最分散,沿海城市的NDIS值接近正态分布,平原城市的NDIS值最集中且呈偏态分布。NCI值的3个箱图中,沿海城市与其他两类相比数值的偏态分布最显著;山地城市与平原城市的数值分布较为集中。

图4 山地、沿海、平原三类城市的NDIS及NCI箱线图Fig.4 Box chart of NDIS and NCI of three types of cities in mountainous, coastal and plain areas*代表类别间在0.05水平上具有显著性差异
一般情况下,NCI值越大,城市越紧凑,而NDIS值越大,城市越离散。35座城市的紧凑度排列位序差异非常大,部分城市的NCI高紧凑在NDIS水平成为了低紧凑。三种地形的城市紧凑水平从NDIS指数来看,山地城市、沿海城市与平原城市的紧凑程度差异显著,总体上呈现的紧凑次序从高到低是平原城市、沿海城市、山地城市。而NCI指示城市的紧凑程度除个别沿海城市偏低之外,三类城市之间的紧凑水平没有显著差异。进一步结合NDIS与NCI共同考察城市的紧凑度,采用K-means均值算法聚类分析得到3个等级的城市紧凑度(图5)。最不紧凑的城市是重庆市、兰州市和大连市。中等紧凑的城市包括天津市、海口市、西宁市、南宁市、武汉市、长春市、哈尔滨市、济南市、昆明市、广州市、贵阳市、杭州市、南京市、青岛市、厦门市、宁波市、深圳市。城市形态最为紧凑的是北京市、上海市、南昌市、郑州市、成都市、福州市、合肥市、呼和浩特市、沈阳市、石家庄市、太原市、乌鲁木齐市、西安市、银川市、长沙市。

图5 35座城市的紧凑度等级Fig.5 Classification of compactness of 35 cities 浅灰代表紧凑度最低的城市,中等灰度代表中等紧凑的城市,深灰代表紧凑度最高的城市; 其中,三角形指山地城市,圆形指平原城市,菱形指沿海城市
3 讨论
NDIS与NCI指示35个城市的紧凑水平具有非常大的差异,正是因为指数的计算逻辑不同,任何计算方式得到的信息都是有限的。兰州市的NCI值达到了0.27,其NDIS却是最高值1.64;大连市NCI值0.17,NDIS值达到了1.5。依据兰州市和大连市的NCI值在35个城市当中的位置,兰州市和大连市均具有相对较高的紧凑度,并不能凸显城市的带状特征。重庆市具有主城+卫星城的组团结构,其NCI值达到0.18,但是其NDIS值却达到了1.62。同样的主城+卫星城结构的北京市,NCI是0.24,NDIS仅有1.2。因此,城市卫星城的规模与距离共同影响了NCI与NDIS值,但是距离的缺陷通过NDIS表现的更加突出,单从这两个指数便能够部分说明主城区的吸引力是否足够强大,卫星城对主城的分担制衡作用是否能够充分发挥。三类城市的箱线图也证明了NDIS值利于解决距离向的问题,而NCI更加权衡了城市斑块面积对城市形态的影响。因此,利用单一指数对这些形态特征突出的城市进行紧凑度的划分放在哪一紧凑水平下都是没有说服力的。NDIS与NCI呈现中等程度的负相关(r=-0.44,P<0.01)。前人研究表明,指数间虽然具有相关性,但更可贵的是其差异性的存在,指数间的差异越大,越利于发现城市形态规律[26]。把NDIS与NCI共同作为考察城市紧凑度的变量,35座城市的紧凑度层次显然更为合理(图5)。由于不同的紧凑度指标计算原理的差异,所指示的紧凑水平也就不同,本文不再与其他研究做对比。
4 结论
本文通过6个情境分析了离散度指数DIS的优缺点,认为DIS值并不能准确地反映城市的紧凑程度,但是运用圆形标准化后的标准化离散度指数NDIS值则具有指示城市空间形态的能力。NDIS不受城市面积规模的影响,以城市斑块的距离为参数,因此城市建设用地的空间尺度对NDIS值影响较小,数值比较稳定。对于城市而言,NDIS具有唯一值,利于城市紧凑度的横向和纵向比较。NDIS值越大,城市越离散。这一特点在案例分析中表现很突出,与NCI形成互补。NDIS并非完美的指数,衡量城市的空间形态仍需要结合更多的格局指数优势互补[27]。
紧凑度指数是对城市空间这一非均质实体的简化和概括,为了证明这些指数的实际意义,需要结合人口、道路、基础设施、公共服务、产业、生态环境等城市内部结构的紧凑性,建立城市问题抽象与具体、理论与实践的关联。中国急需发展紧凑的城市形态,我们强调的紧凑城市是在合理的紧凑范围内,适度的紧凑有利于资源、基础设施的共享,降低城市运行的成本,实现城市的可持续发展。而过于紧凑的城市生态环境压力过大,影响城市生态系统稳定和居民生活质量。今后研究应结合多种形态指数对中国主要城市的紧凑程度进行归纳总结,找出城市之间的共同点和适度的紧凑区间,为紧凑城市、可持续城市和低碳城市的建设提供参考。
