浅水区海底管道周围海床孔压分布数值计算研究

付长静，吕 毅，赵天龙，车 权，聂玉玺

(1. 重庆交通大学 河海学院，重庆 400074； 2. 国网重庆市电力公司 重庆 400014)

0 引 言

由于当今陆地油气资源的日渐短缺，海洋油气资源的开发已引起了国内外的高度重视。近些年，我国于渤海湾区域、东海、珠江口、北部湾、南海建成投产了许多大中型油田。随着油田的建立，各种海底管道的建设也逐步发展。我国海上石油开采起步较晚，目前大多数油田都建在近岸浅水区域。由于浅水区波浪的非线性影响显著，浅埋管道受非线性波浪荷载的影响大。波浪的传播造成海床面波压力随周期变化，而波压力会进一步传递到海床中，引起超静孔隙水压力和附加有效应力，改变了海床中有效应力的分布。极端海况下，海底砂土可能由于土中超静孔隙水压力或波动经过时产生的渗流而发生液化。一旦海床土发生液化，管道的支撑条件就会改变，使管道产生变形，甚至发生事故。因此针对我国国情，为了合理地评价海底管道在波浪作用下的稳定性，需要充分考虑浅水区波浪的特性[1]，建立浅水波作用下海底管道周围海床动力响应数学模型。近年来，许多学者开始关注波浪的非线性对管道的影响，建立的数学模型考虑了管-土间的相互接触作用和孔压的累积效应，采用弹塑性本构模型，使得数值计算结果更加真实可信。F. P. GAO等[2]考虑了波浪的非线性，建立了非线性波浪作用下埋置管道周围海床孔压瞬态响应模型。栾茂田等[3-4]考虑了管-土间的相互接触效应、认为管道可变形，在线性和非线性波浪条件下，采用有限元方法建立了管道周围海床动力响应的数值模型，分析了土体的相关物理指标对管道周围海床超静孔隙水压力的影响。H. MAHMOOD等[5]考虑了波浪的非线性，利用有限元分析了浅水区埋置管道的稳定性。随着科学技术的发展，大型商业软件已经成为解决工程实际问题的重要手段。任艳荣等[6-7]依靠ABAQUS软件，考虑了管-土的相互接触效应，采用弹塑性本构模型，分析了环境荷载和管重对管道稳定性的影响。目前在研究海底管道稳定时，大都采用stokes波浪理论，但stokes波浪理论适用于深水区，当水深较浅(L/d>8，其中L为波长，d为水深) 时，stokes波浪理论就已经不再适用，更适合采用孤立波理论(L/d>40)或椭圆余弦波理论(L/d>40)[8-9]。

1 管道周围海床动力响应数值模型

1.1 模型假设

如图1，考虑深度为h海床，假设海床底面为不透水，海床中埋置管道的半径为R，埋置深度为dp。波浪沿x方向传播，z坐标自海床底起向上。本文基于Biot固结理论，通常有如下假定：(1)土体骨架变形满足胡克定律；(2)孔隙水为无粘性流体；(3)土体各向同性； (4)海床上部波浪场是无旋的；(5)土体内部渗流满足达西定律；(6)土体的渗透系数为常数；(7)管道管壁不透水；(8)海床面上部水层不可压缩。考虑到波浪引起的海床运动为相对静水平衡状态下的微小振荡，因此认为上述假定是合理的。

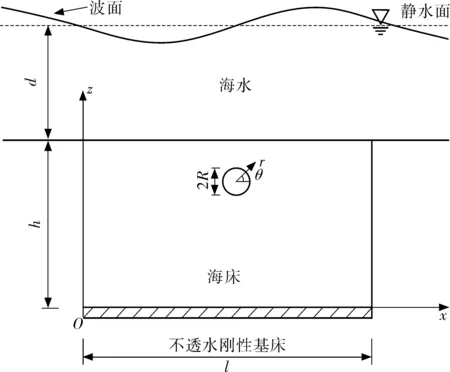
图1 管道与海床相互作用数值模型示意Fig. 1 Schematic diagram of numerical model of mutual effectbetween pipelines and the seabed

1.2 控制方程

通常多孔介质的连续方程可表示为：

(1)

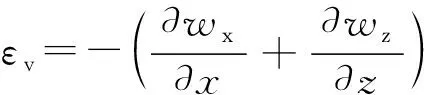
在进行计算时，假定土体的渗透系数为常数，式(1)变为：

(2)

通常由孔隙水压力和位移表示的土体平衡方程为[10]：

(3)

(4)

式中：wx与wz为土体的位移;υ与G分别是土体的泊松比和剪切模量。

1.3 模型边界条件

根据图1可知，为了研究管道周围海床土的瞬时响应，需要考虑海床的边界条件，包括海床面、海床底及海床两侧的边界条件，同时需要考虑管道表面的边界条件。

1)海床表面边界条件：海床表面的超静孔隙水压力近似等于波浪在海床表面所引起的波压力[11]，即：

(5)

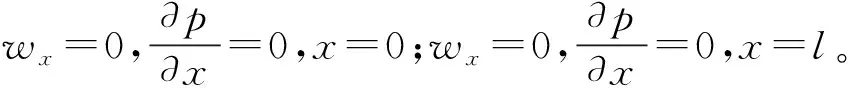
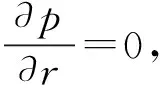
(6)

2 管道与海床相互接触作用模拟

管道与海床的接触具有表面非线性特性。由于管道材料的强度远大于土体强度，在计算时通常认定管道表面为接触主面，而土体界面为接触从面。对于法向作用，主要采用硬接触，即压力直接进行传递，没有衰减。同时，当接触压力值小于0时，认为接触面上的点断开。对于切向作用，主要是摩擦作用，在ABAQUS中默认采用Coulmob定律，接触面间的摩擦特性用摩擦系数来表示。采用该理论时，认为当接触面处于闭合状态时，接触面存在摩擦力。

3 地应力平衡分析

利用ABAQUS计算软件，采用关键字定义初始地应力法，给出海床最高和最低点的自重应力以及相应位置处的坐标。当几何模型较规则时，可以采用这种方法，并且在施加初始应力场时，可以依据水平方向的侧压力系数来控制，平衡的结果如图2。

图2 地应力平衡结果Fig. 2 Result of earth stress balance

在进行地应力平衡后，土体的位移量级达到10-4m，认为初始地应力平衡结果可以接受，对后续的分析工作影响较小(土体不能发生较大的变形)。通过上面的计算结果可以看到，经过自重应力平衡后，海床的竖向位移最大为10-6m量级，达到预期目的。

4 网格划分

模型中，与管道接触的土体选用孔压/位移耦合的CPE8RP单元，其他土体选用位移-孔压耦合4节点平面应变CPE4P单元，管道选择线性减缩积分平面应变CPE4R单元。考虑管道与土体的接触效应，在划分网格时，将与管道相接触的土体部分的网格进行加密处理，模型网格的划分情况见图3，管道的网格划分如图4。

图3 模型网格Fig. 3 Grid diagram of model

图4 管道网格Fig. 4 Grid diagram of pipelines

5 计算结果分析

管道的位置分布如图5，计算参数见表1。

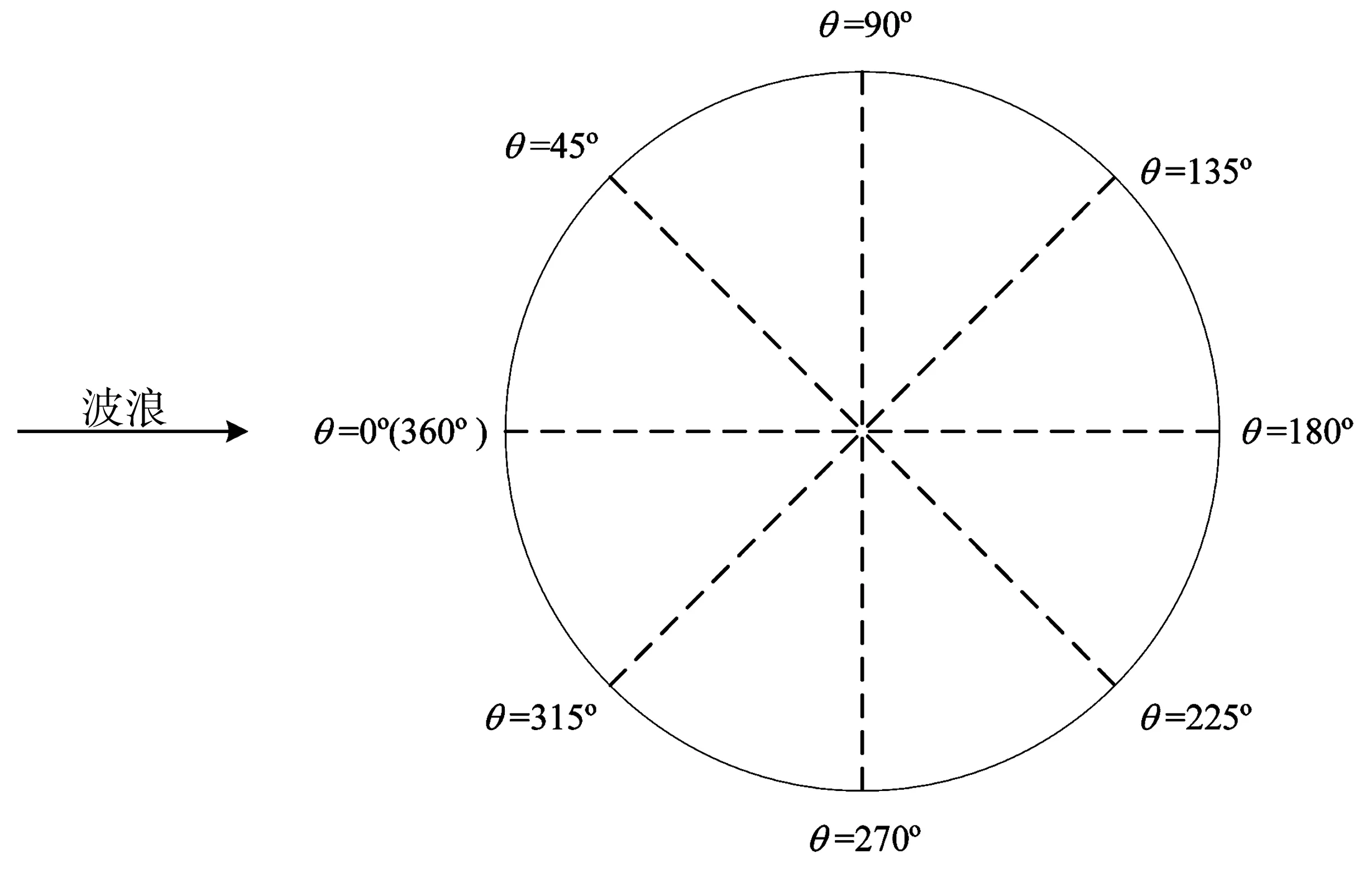
图5 管道位置分布示意Fig. 5 Schematic diagram of pipeline position distribution

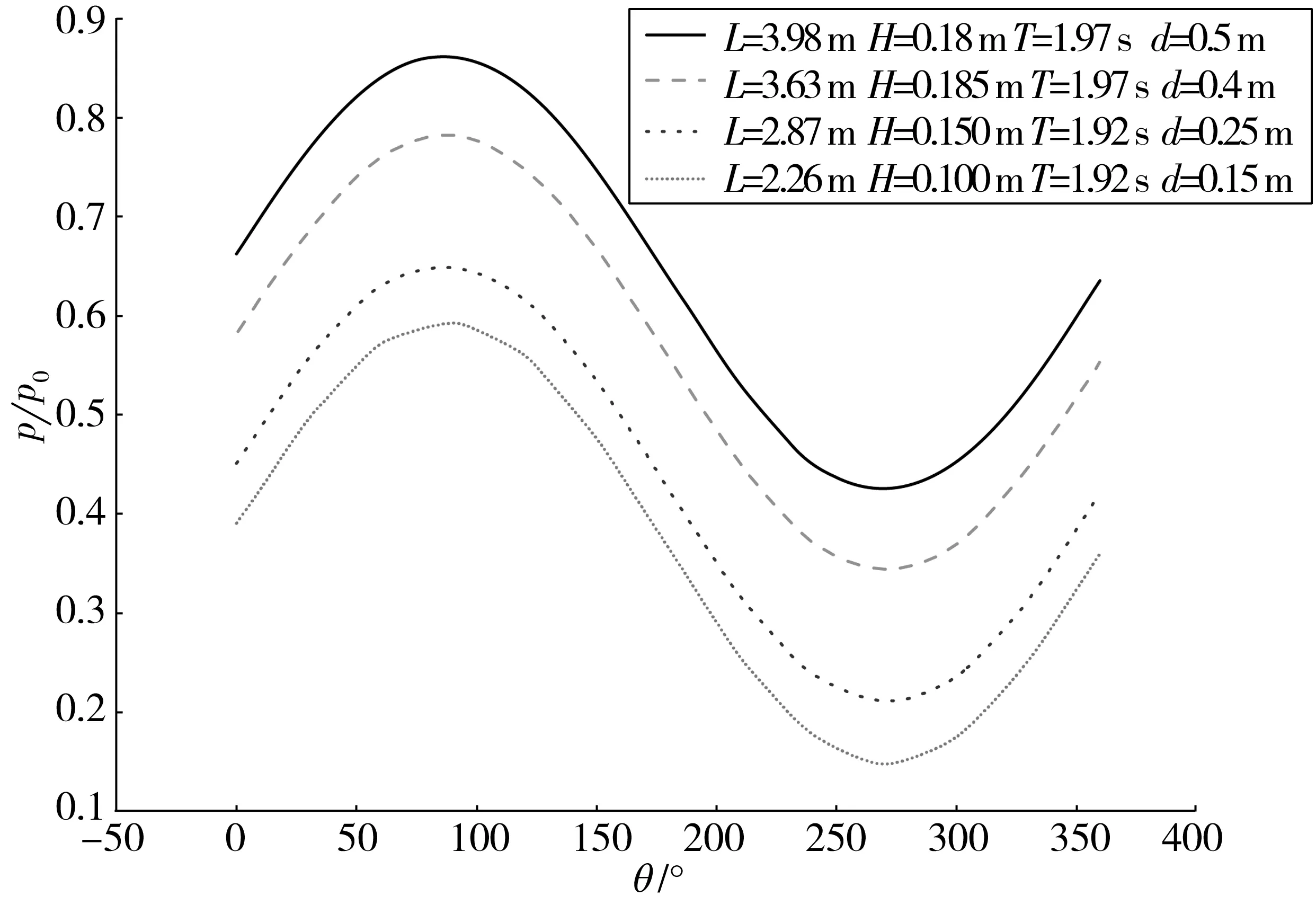
图6 管道周围海床超静孔隙水压力比分布Fig. 6 Distribution of wave induced excess pore water pressure in seabed around pipelines

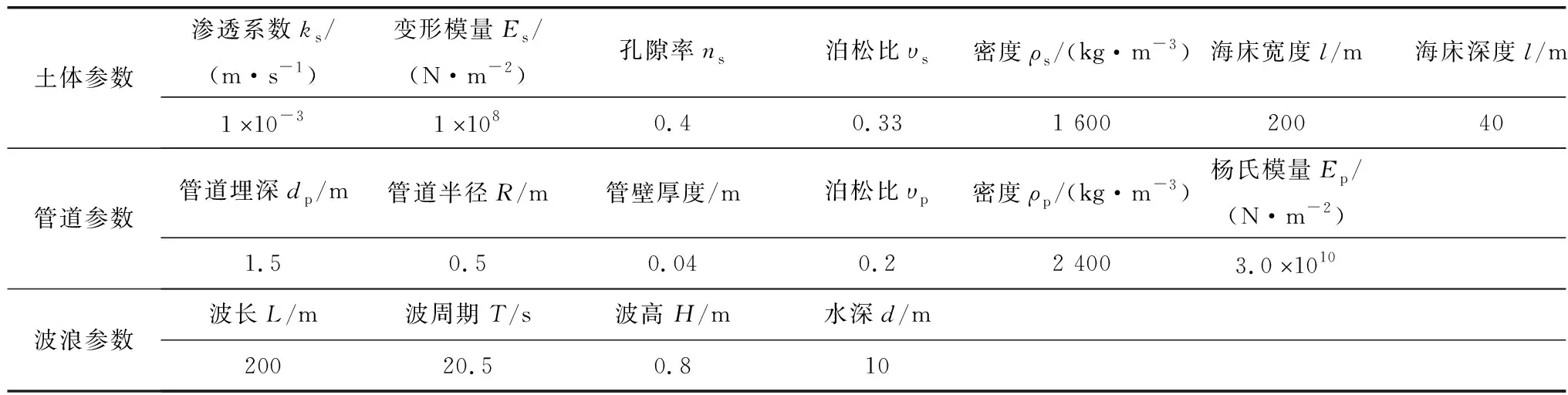
表1 计算参数Table 1 Mechanical parameters

计算给出波浪作用下管道周围海床超静孔隙水压力并进行归一化处理，得到波浪作用下管道周围海床超静孔隙水压力比分布，如图6。从图6可以看出，数值计算得到的管道周围的超静孔隙水压力呈明显的正弦分布。计算结果显示，管道上最大压强出现在管道顶部，最小值出现在底部，并且管道周围压强值随着水深的增加而增大。

6 影响因素分析

由于埋置管道周围海床土体中超静孔隙水压力与海床土本身的性质等因素有关，本节重点分析影响管道周围土体超静孔隙水压力计算结果的各因素。计算输入数据见表1。

6.1 管道与海床的接触效应的影响

为研究管道与海床的接触对管道周围海床超静孔隙水压力的影响，分别计算两种情况下管道周围海床的超静孔隙水压力比分布，如图7。从图7中可以看出，管道与海床之间的接触效应对由波浪引起的管道周围海床超静孔隙水压力影响非常小，两种情况下超静孔隙水压力比基本相同。

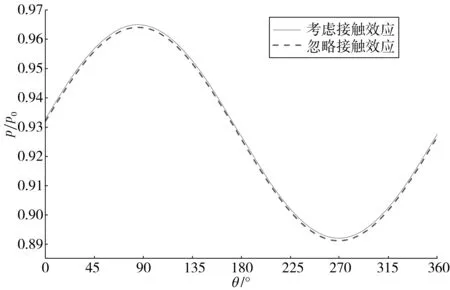
图7 考虑及忽略接触效应时管道周围海床超静孔隙水压力比分布Fig. 7 Distribution of excess pore water pressure ratio by consideringor neglecting pipe-soil contact effect

6.2 海床渗透系数的影响

针对不同渗透系数的土体，图8给出由波浪所引起的管道外表面周围土体中超静孔隙水压力比分布。从图8可以看出，随着土体渗透系数的减小，波浪引起的管道顶部及底部处的超静孔隙水压力差值却逐渐变大，这表示减小土体的渗透系数，在波浪的作用下可能会加大管道周围土体失稳的可能性。

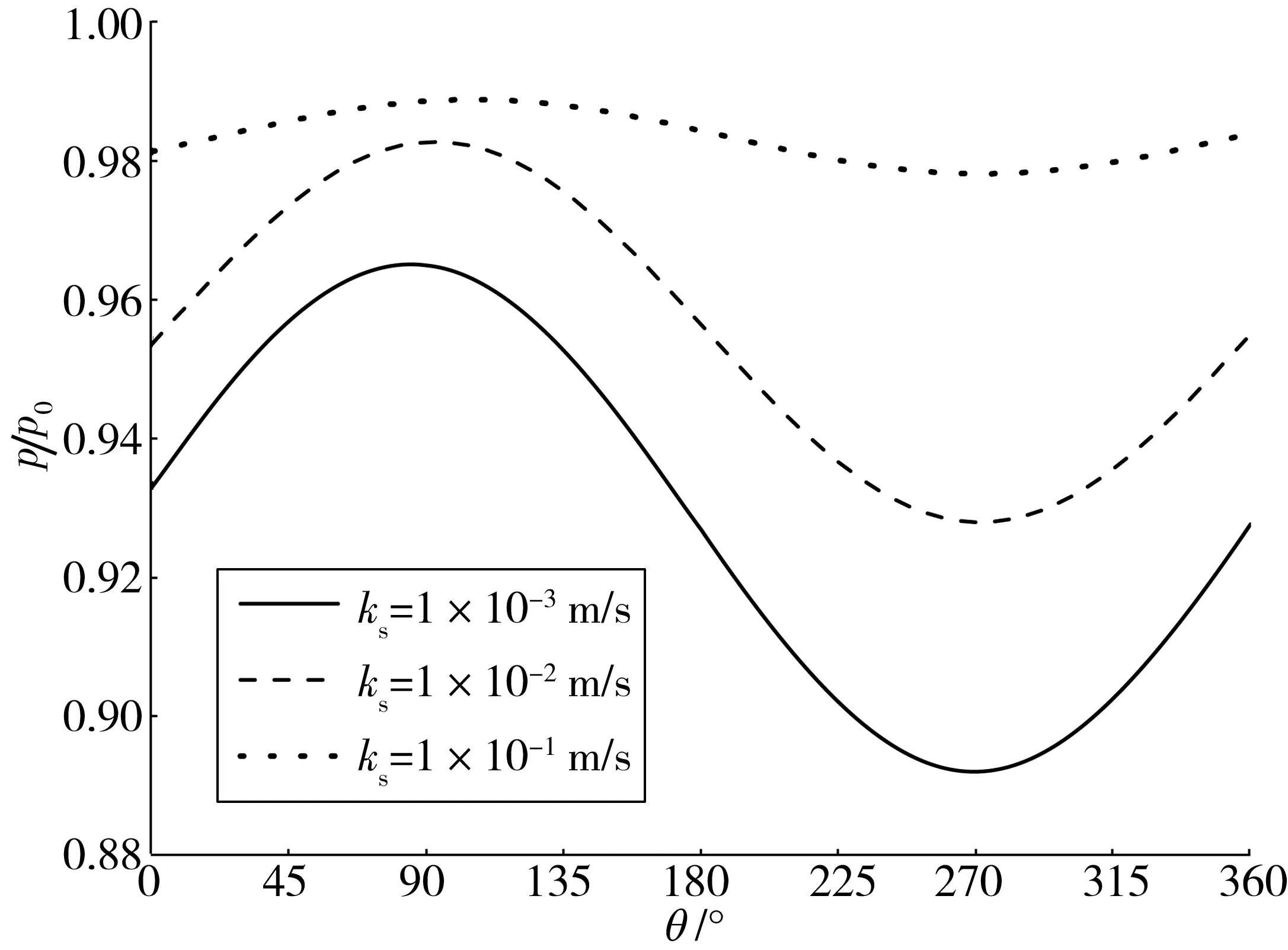
图8 不同渗透系数下管道周围海床超静孔隙水压力比分布Fig. 8 Distribution of excess pore water pressure ratio under the condition of different permeability coefficients

6.3 海床弹性模量的影响

考虑海床弹性模量的影响，图9给出了不同弹性模量的土体中超静孔隙水压力比分布。从图中可以看出，随着弹性模量的增大，管道周围海床土的超静孔隙水压力逐渐减小，并且管道顶部与底部处的超静孔隙水压力差值也相应减小。这是由于土体的弹性模量影响土体受力后的位移，而土体的位移会对土体内部孔隙流体的渗入和排出产生直接的影响。

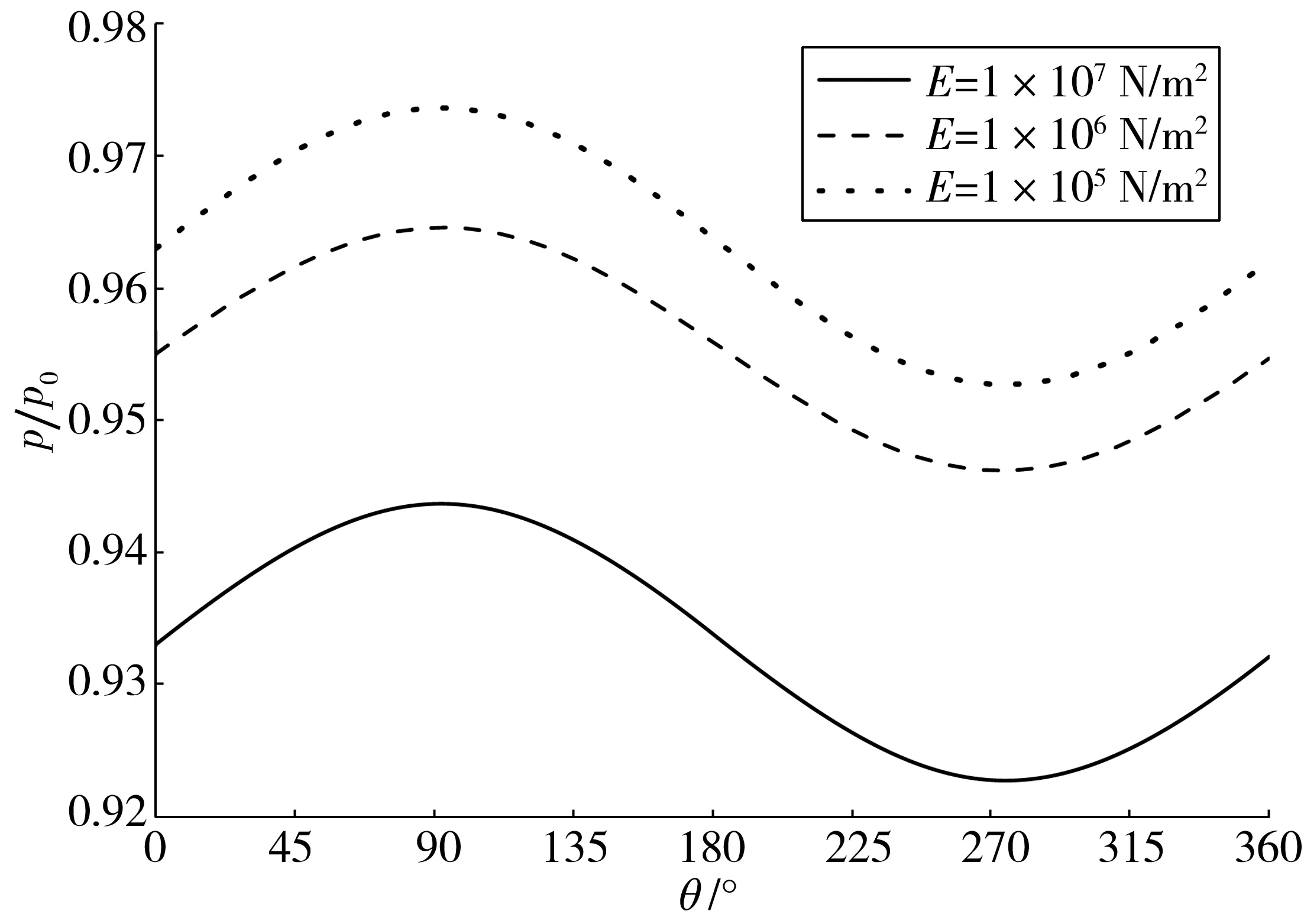
图9 不同弹性模量下管道周围海床超静孔隙水压力比分布Fig. 9 Distribution of excess pore water pressure ratio under the condition of different elastic modulus

6.4 海床孔隙率的影响

针对孔隙率不同的土体，给出波浪引起的管道外表面周围海床中超静孔隙水压力比分布，如图10。从图中可以看出，随着土体孔隙率的减小，由波浪引起的管道上部与下部的超静孔隙水压力差值却逐渐变大。这表示土体孔隙率减小时，波浪荷载可能会增加管道周围土体失稳的可能性。

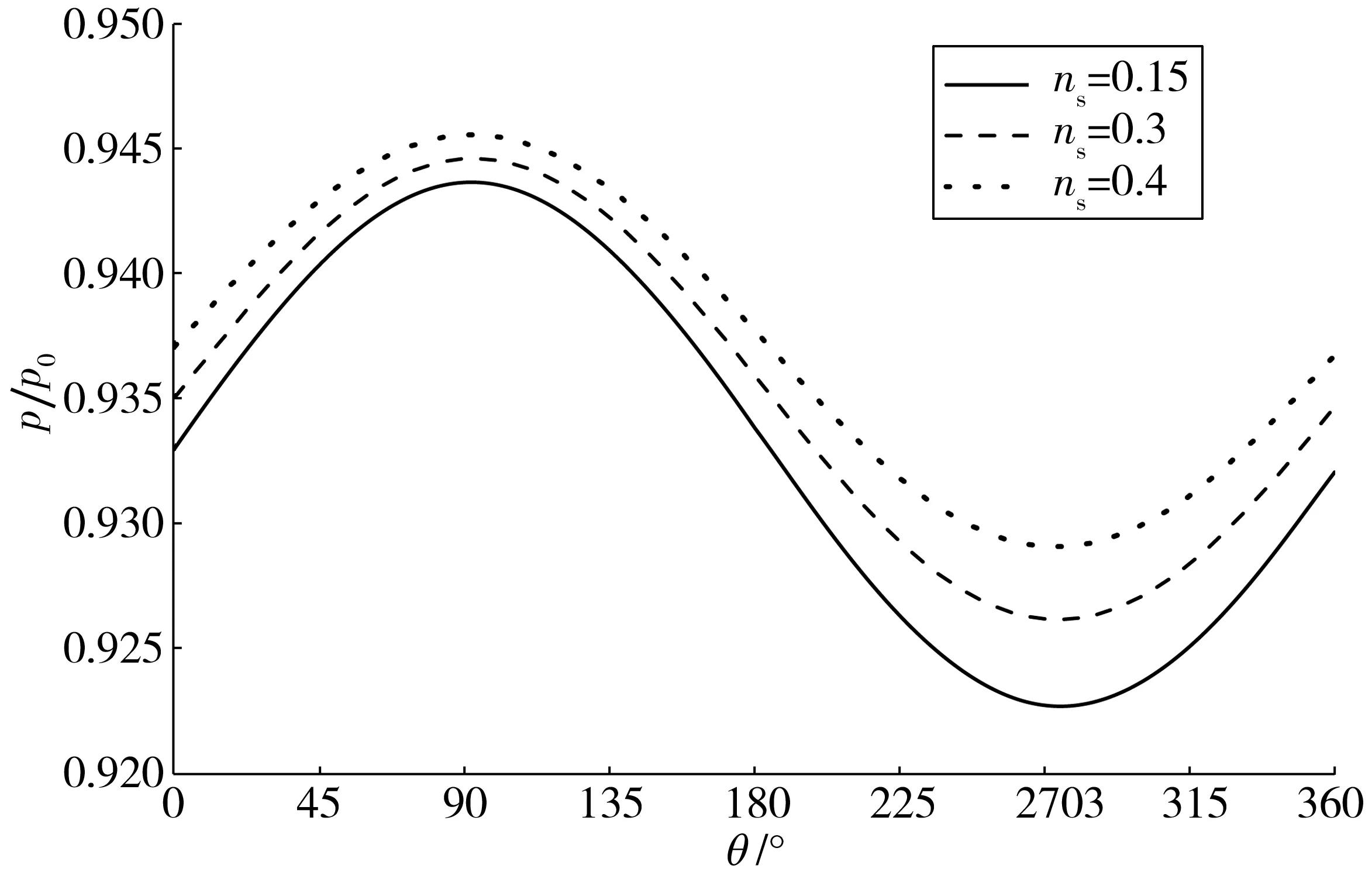
图10 不同孔隙率下管道周围海床超静孔隙水压力比分布Fig. 10 Distribution of excess pore water pressure ratio under the condition of different porosity

6.5 海床泊松比的影响

考虑海床泊松比的影响，图11给出了波浪引起的管道外表面周围海床中超静孔隙水压力比分布。从图中可以看出，土体的泊松比对管道周围海床中超静孔隙水压力影响非常小。在不同泊松比的土体中，波浪引起的管道周围海床中超静孔隙水压力基本相同。

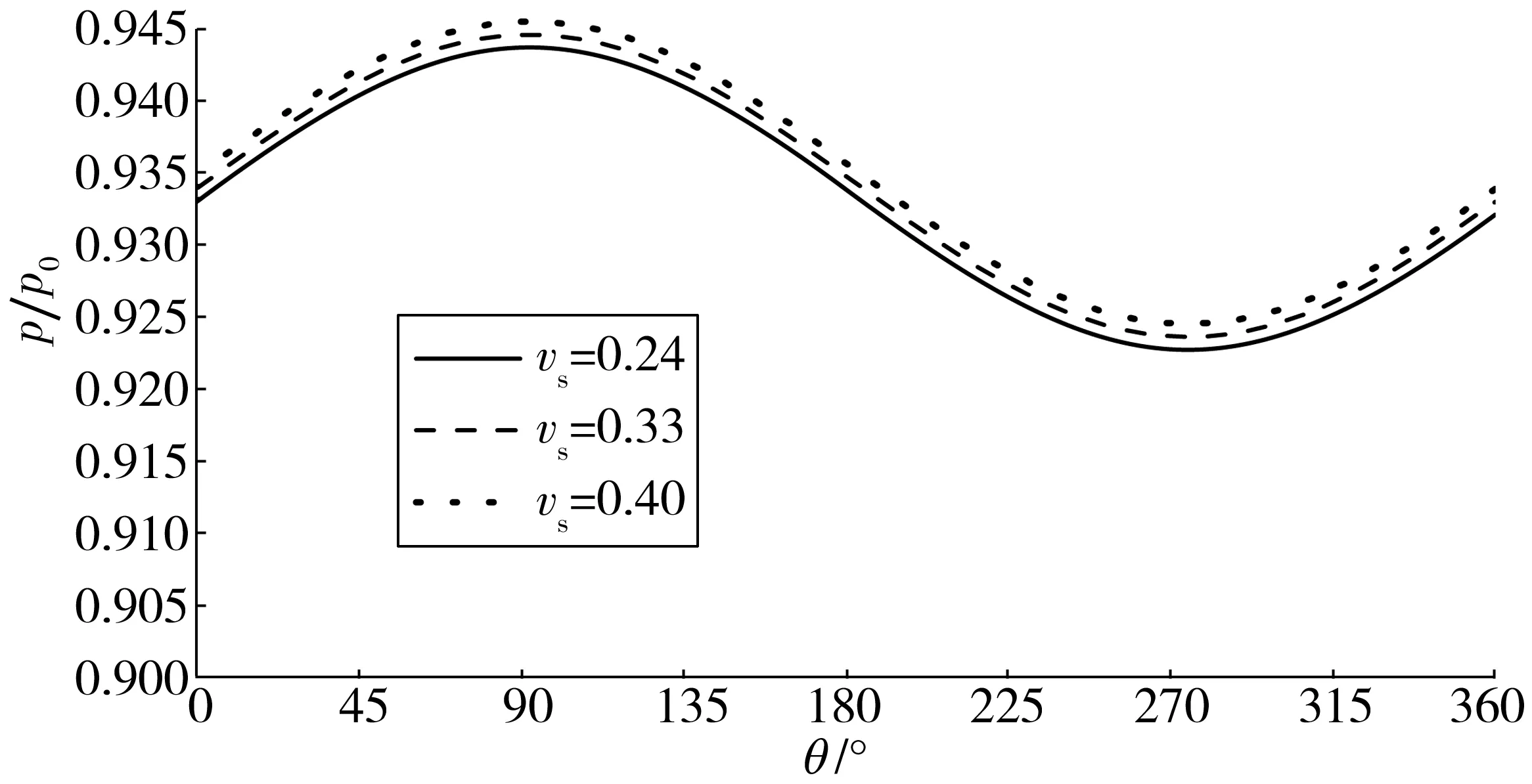
图11 不同泊松比下管道周围海床超静孔隙水压力分布Fig. 11 Distribution of excess pore water pressure ratio under the condition of different Poisson’s ratio

6.6 管道埋置深度的影响

针对不同的埋置深度，图12给出由波浪所引起的管道外表面周围海床中超静孔隙水压力比分布。从图中可以看出，随着埋置深度的不断增加，波浪引起的管道周围海床中超静孔压不断减小，且管顶及底部超静孔压差值也相应减小。这表明管道周围土体发生破坏的可能性也就越低，也就是埋置深度越大，管道越安全。

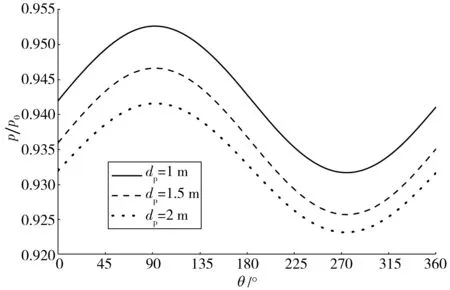
图12 不同埋深下管道周围海床超静孔隙水压力分布Fig. 12 Distribution of excess pore water pressure ratio under the condition of different embedded depths

7 结 论

以埋置管道为研究对象，考虑管道为弹性及管道与海床的接触作用 ，建立了浅水区埋置管道瞬态响应有限元模型，通过对ABAQUS计算软件进行二次开发，引入一阶近似椭圆余弦波作用于海床面上的波浪荷载。计算分析发现，管道与海床的相互接触效应对于波浪作用下管道周围海床中超静孔隙水压力的分布影响非常小，而海床的渗透特性、孔隙率、弹性模量以及埋置深度对管道周围海床中超静孔隙水压力分布有明显影响。当海床的渗透性越低、弹性模量越小、埋置深度越浅，管道周围土体越容易发生失稳。因此在铺设管道之前应充分了解海床的地质条件，考虑海床土的物理性质指标，选择合适的施工场地进行管道铺置。