单缆悬索桥成桥及施工阶段非线性静风响应

乔云强，付 曜

(1.林同棪国际工程咨询(中国)有限公司，重庆 401121； 2.长安大学 公路学院，陕西 西安710064)

0 引 言

悬索桥整体结构刚度较小，特别是处于施工阶段的悬索桥对风的作用更为敏感。日本东京大学A. HIRAI等[1]早在1967年就在风洞试验中发现了悬索桥静力扭转发散的现象；在汕头海湾二桥的试验中同济大学风洞实验室同样发现了由静风引起的斜拉桥静力失稳现象[2-3]。此后，多位国内外学者对静风稳定问题进行了研究[4-6]。JTD/T D 60-01—2004《公路桥梁抗风设计规范》中也基于线性的方法给出了侧倾失稳和扭转失稳临界风速的计算公式。随着有限元方法的发展，程进等[7]进一步提出了综合考虑几何非线性、静风荷载非线性和材料非线性的静风稳定性分析方法。此后多位学者对非线性的静风稳定性进行了研究[8-10]，但目前国内对于单主缆双幅大跨度悬索桥研究较少，特别是施工阶段的静风稳定性研究，笔者基于某实际案例，在风洞试验的基础上，对大跨度单缆悬索桥成桥状态及施工状态进行了三维非线性静风响应的计算，并对其静风稳定性进行了研究。

1 有限元模型的建立

某景观大桥为单跨400 m单主缆悬索桥，采用“山”型索塔。加劲梁为分离式变间距双钢箱结构，梁宽由跨中处19 m变化为桥塔处36 m。主缆矢跨比为1/9，吊索间距为10.5 m，跨中段采用竖直吊杆，靠近桥塔处采用斜吊杆，主跨跨中桥面距水面高度为29.5 m，桥面高度处的设计基准风速39.7 m/s，地表分类按A类取值，地表粗糙度系数α=0.16，大桥效果见图1，立面见图2。

图1 大桥效果Fig. 1 Effect of the bridge

图2 大桥立面(单位：m)Fig. 2 Elevation view of the bridge

大桥加劲梁为分离式箱梁，由吊索处的横梁连接成整体，可建立双主梁有限元模型。由于桥梁静风稳定性计算用的静三分力数据是根据节段模型试验得到的，如果直接加载到双主梁有限元模型上，其加载方式繁琐且不精确。为便于该单缆大跨度悬索桥的静风稳定性分析，笔者采用通用有限元程序ANSYS建立了该桥单主梁有限元模型(图3)。

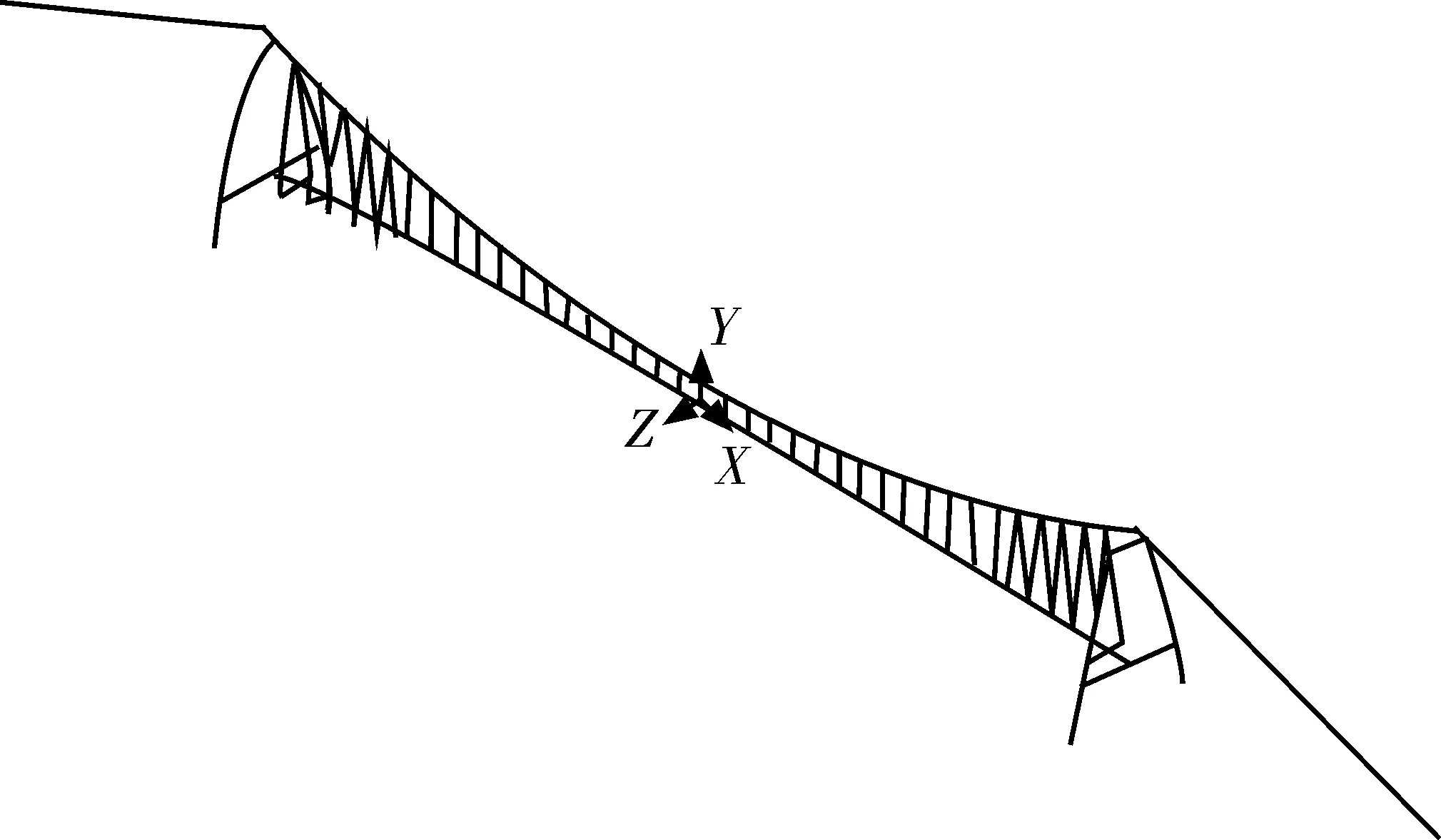
图3 单主梁有限元模型Fig. 3 Finite element model of single girder

表1为单梁模型与双梁模型频率误差和振型描述的对比结果。

表1 单双主梁模型频率振型对比Table 1 Comparison of single and double main beam model

由表1可知，单梁模型和双梁模型主要振型和频率的误差较小，即建立的单梁模型符合该桥的结构特点，可用于静风稳定性计算。

悬索桥主梁架设顺序一般分两种方案：从跨中向两侧桥塔推进；从两侧桥塔向跨中推进。由于单主缆悬索桥在不加抗风措施情况下无法保证第1种方案施工阶段的抗风稳定性，因此推荐采用主梁从两侧桥塔向跨中的架设顺序，建立了主梁拼装率分别为30%、60%、90%、100%(不考虑二期荷载)时的施工阶段有限元模型。

2 静三分力试验

由于该桥为分离式变间距双箱截面，对于节段模型只能取有代表性的典型主梁节段进行试验，对于测力试验，选取了桥塔位置处、1/8跨径、1/4跨径及跨中4个典型主梁节段，即主梁间距最大，最小，及中间的两个过渡点，如图4。试验在长安大学风洞试验室进行，获得的各节段模型的静三分力系数如图5、图6。根据4个典型断面的结果，线性插值得到桥轴线上不同位置的三分力系数。在计算过程中，根据主梁各点在桥轴线上的位置选取对应的三分力系数，对主梁进行静风响应分析。

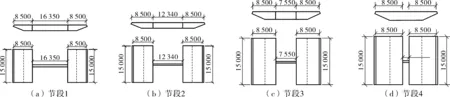
图4 主梁各节段横断面与立面图Fig. 4 Transection view and elevation view of each section of main beam

图5 均匀流场下主梁各节段的三分力系数(施工阶段)Fig. 5 Static coefficients of main girder(construction)

图6 均匀流场下主梁各节段的三分力系数(成桥阶段)Fig. 6 Static coefficients of main girder(completed)

3 非线性静风稳定性的分析

基于风洞试验得到的静三分力系数，采用增量与内外两重迭代相结合的方法，用ANSYS的APDL语言进行了二次开发并编制了相应的程序，静风响应的计算流程[8]如图7。失稳风速的判定依据：①迭代过程中，三分力的欧几里德数是否小于0.005；②更重要的是，随风速变化的主梁响应(竖向和横向位移、扭转变形)曲线的斜率是否突然增大，一般达到75°以上。若三分力的欧几里德数均小于0.005且响应曲线的斜率较小，则认为结果收敛；反之，若三分力的欧几里德数大于0.005且响应曲线的斜率已非常大，则认为静风响应计算结果发散，该风速计可作为失稳风速。

图8～图12为风速对各状态下横梁静风响应的影响。

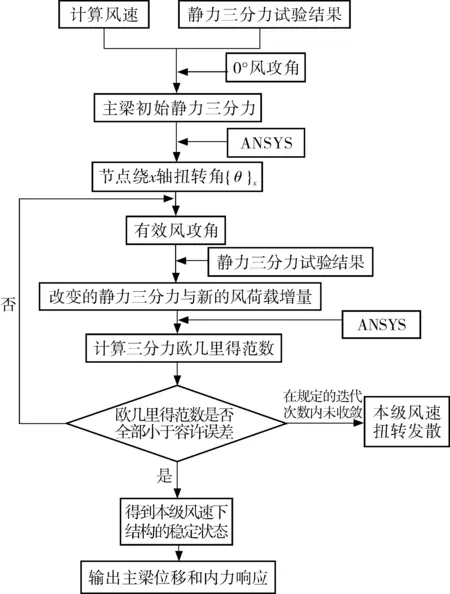
图7 计算流程Fig. 7 The calculation process

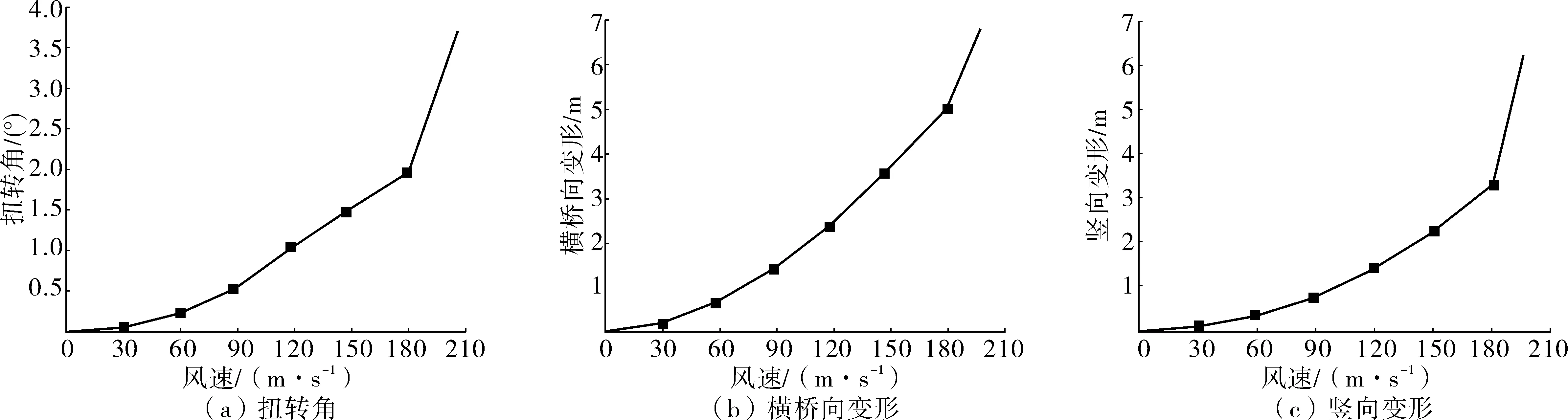
图8 不同风速对成桥状态静风响应的影响Fig. 8 Effects of wind speed on static wind response

图9 不同风速对100%施工阶段的影响Fig. 9 Effect of wind speed on 100% construction stage

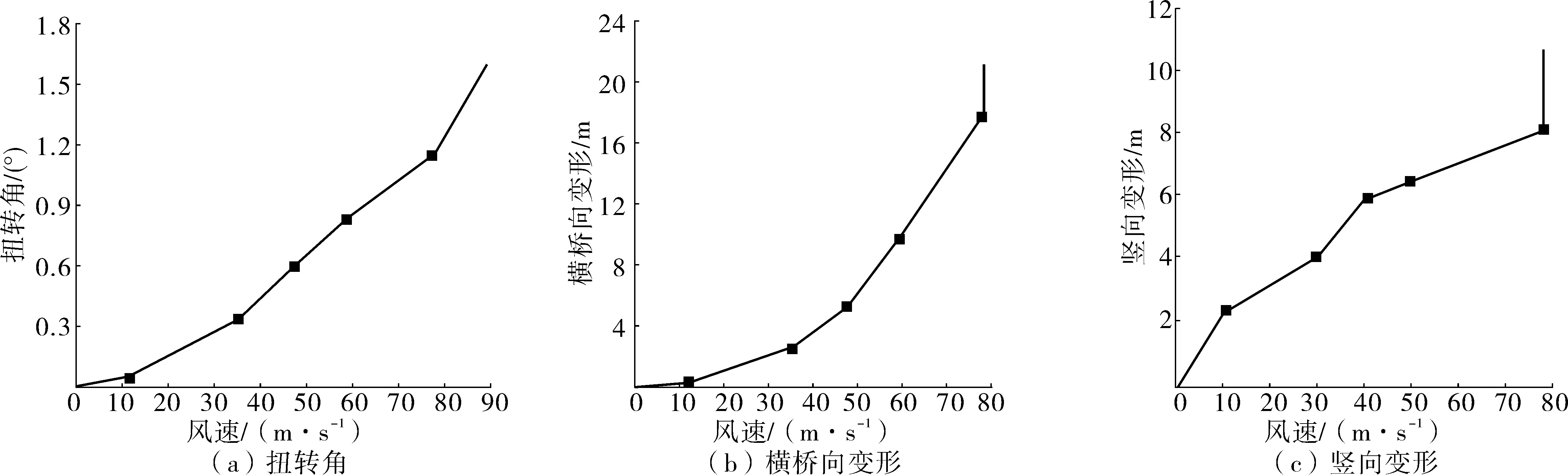
图10 不同风速对30%施工阶段的影响Fig. 10 Effect of wind speed on 30% construction stage

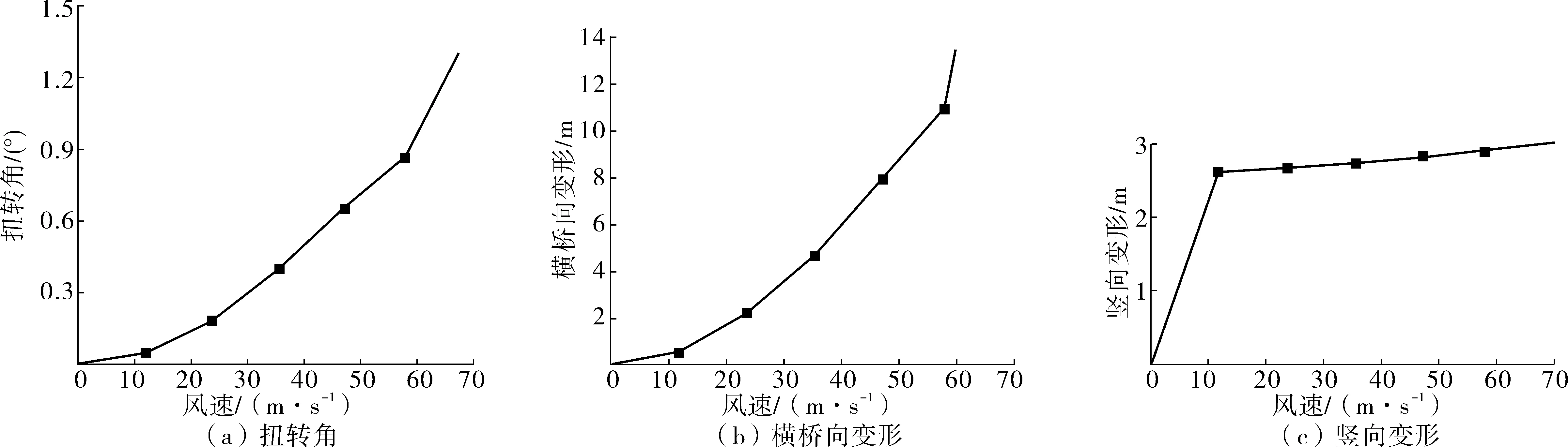
图11 不同风速对60%施工阶段的影响Fig. 11 Effect of wind speed on 60% construction stage

图12 不同风速对90%施工阶段的影响Fig. 12 Effect of wind speed on 90% construction stage

表2给出了各施工阶段的静风失稳临界风速。

表2 各阶段失稳风速Table 2 Steady wind velocity at each stage m/s

4 非线性静风响应的计算

图13～图17为不同风速下成桥及各施工阶段的静风响应结果。从图13～图17可知，随着风速的增加，主梁扭转、横桥向和竖向变形呈递增趋势，其最大响应均出现在临近跨中位置，并向两端逐渐减小。

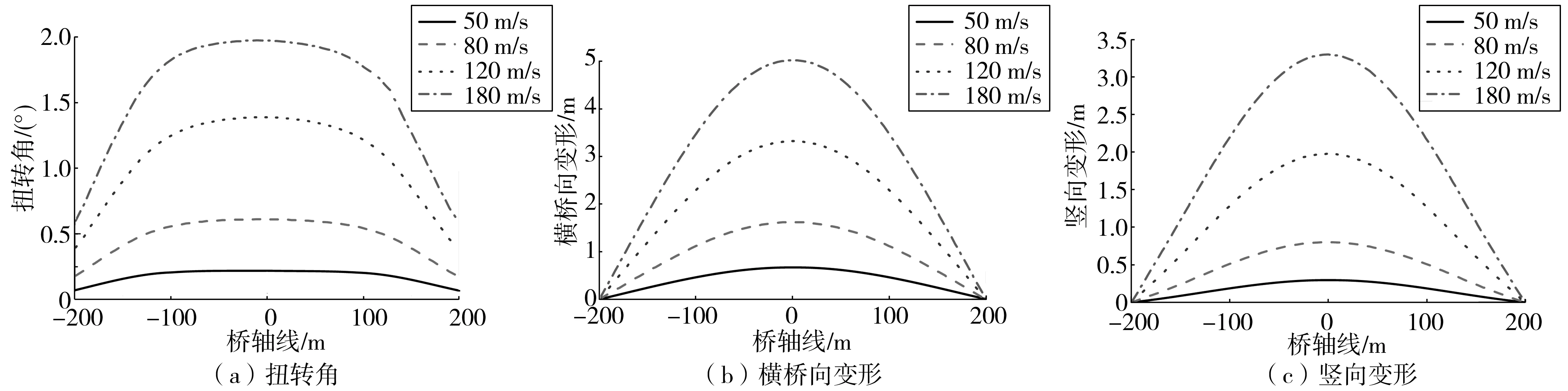
图13 不同风速下成桥状态的静风响应Fig. 13 Static wind response of bridge under wind speeds

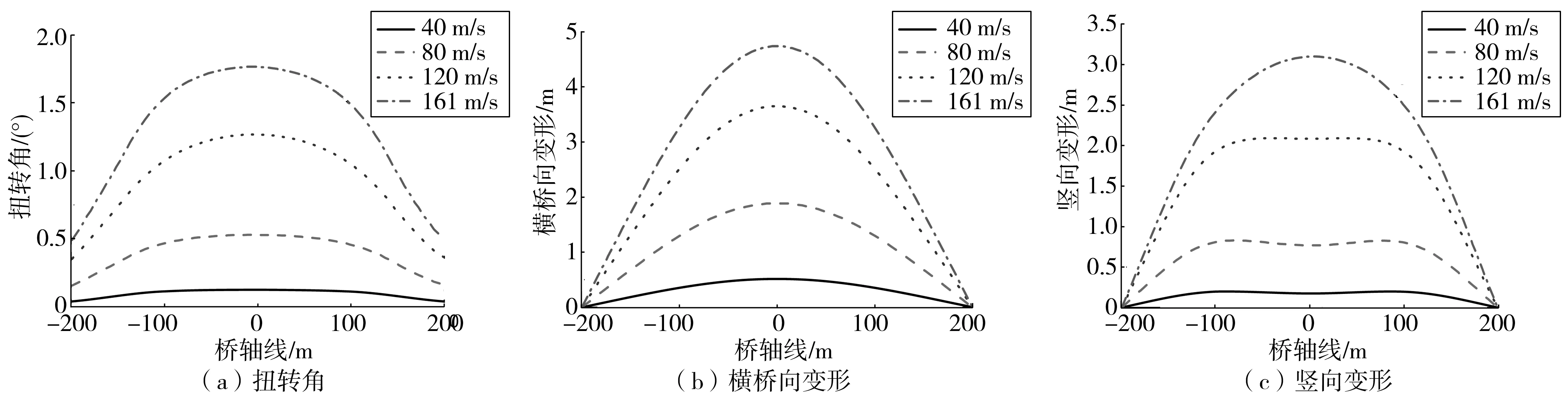
图14 不同风速下100%施工阶段的静风响应Fig. 14 Static wind response of 100% construction stage

图16 不同风速下60%施工阶段的静风响应Fig. 16 Static wind response of 60% construction stage

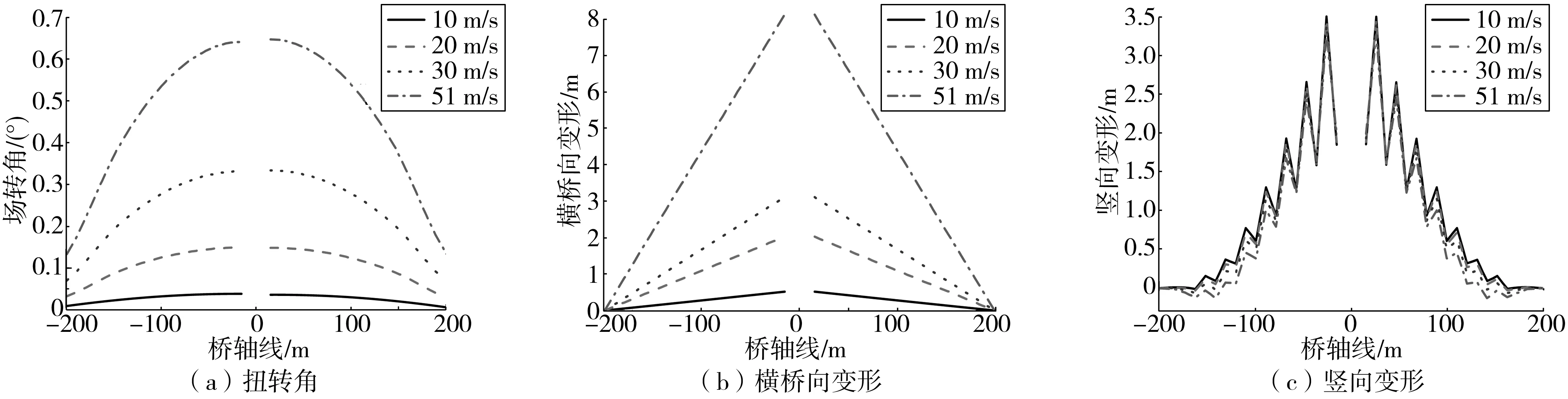
图17 不同风速下90%施工阶段的静风响应Fig. 17 Static wind response of 90% construction stage

5 结 论

通过建立某单缆大跨悬索桥不同施工阶段和成桥状态的有限元计算模型，分析研究该桥型非线性静风稳定性及非线性静风响应，得出如下主要结论：

1)单缆大跨悬索桥施工阶段的静风失稳临界风速随着主梁拼装率的增加而降低，在即将合拢前达到最小。因此，应注意施工过程中，特别是即将合拢时的静风响应。

2)单缆大跨悬索桥施工阶段的主梁最大扭转角、横桥向和竖向位移，均发生在靠近跨中的主梁吊装段，并向两边逐渐减小。

3)成桥后，由于主梁梁段间由临时连接转变为刚接以及二期荷载的施加，使得结构刚度大幅提升，使得静风响应不会对成桥状态的单缆大跨悬索桥产生较大影响。

上述施工阶段的静风失稳风速及结构响应是主梁由桥塔向跨中方向架设方案的计算成果，结果显示该架设方案静风稳定性满足安全要求。如采用由跨中向两侧桥塔方向架设方案，需增加主梁抗风稳定措施，其施工阶段静风稳定性可做进一步研究。