基于可靠性的导流洞堵头设计优化分析

汪 魁，刘 欢，罗 盈

(1. 重庆交通大学 水利水运工程教育部重点实验室，重庆 400074； 2. 重庆交通大学 高校水工建筑物健康诊断技术与设备工程研究中心，重庆 400074；3. 重庆市水利电力建筑勘测设计研究院，重庆 401121； 4. 四川大学 水利水电学院，四川 成都 610065)

0 引 言

可靠性理论在土木工程结构中的应用研究开始的比较早，国外关于结构可靠性的研究开始于1911年，而我国则是在国外已将结构可靠度问题研究进展到了一定深度时，才处于起步阶段。虽然起步较晚，但是我国工程结构可靠性理论与应用发展迅速，成果显著[1]。

近年来，可靠性理论在工程结构设计计算中不断得到应用，尤其是在工程结构设计中，逐渐从以经验为主的安全系数法到以概率分析为基础的极限状态设计法的“ 转轨”。在水利工程和岩土工程中，可靠性理论的应用研究不断深入，尤其是以概率论为基础的极限状态设计方法被大量借鉴用以工程设计和分析中[2-6]。如向阳生[2]，郑江[3]分别针对水工隧洞围岩稳定性，采用Monte-Carlo法对隧洞结构进行可靠度研究；范书立等[4]、徐强等[5]分别针对地震作用下重力坝结构体系的失效路径及结构可靠性开展了研究；彭辉等[6]研究了已建重力坝抗力与荷载效应随时间变化的规律，推求了大坝整体失效概率。总之，进一步推动可靠性理论在水工结构设计中的应用具有重要的理论意义和工程实际价值。

目前，在水工隧洞堵头设计方面还没有统一的标准和设计准则，虽然已知其等级(即相应的水工建筑物等级)，却并无相关设计条款可以参考，故设计人员在确定堵头设计参数时，出于对整个工程的安全着想，往往选择一些偏于安全的参数，而其中最重要的参数——堵头的长度也是过于保守，致使工期更趋紧张，有时还可能造成赶工，在一定程度上增加了施工风险的同时，也增加了造价[7-12]。因此，考虑将可靠性理论引入到水工隧洞堵头的设计计算中，建立基于可靠性理论的堵头设计参数优化分析方法。

1 基于极限状态的堵头设计可靠性理论

在结构可靠度分析和设计中，使用结构的极限状态作为结构可靠和失效的界限来描述结构的工作状态。假定堵头结构的抗力随机变量为R，荷载效应随机变量为S，则堵头结构的极限状态方程可以表示为

Z=g(R,S)=R-S=0

(1)

在水工隧洞堵头稳定性分析常用的计算方法中，主要有抗滑稳定安全系数法、圆柱面抗冲剪法、整体安全系数法和点安全系数法[6]，在此基础上可以分别建立几种不同类型水工隧洞堵头的极限状态方程。考虑堵头结构的抗力为堵头与围岩之间的摩擦力和材料黏聚力，荷载效应为堵头上游断面所受水平方向的合力，那么可建立堵头的抗滑极限状态方程为

Z=N·f+α·AC-∑PH=0

(2)

式中：N为滑动面法向力，MN；f为抗剪断摩擦系数；α为黏结有效面积系数；A为有效承剪面面积，m2；C为黏聚力，MPa；∑PH为水平方向合力，MN。

通过有限元数值分析得到接触面上的法向应力和剪应力，将法向应力视为抗力，剪应力视为荷载效应，得到堵头的整体稳定极限状态方程为

Z=∑σnifAi+∑CAi-∑τiAi=0

(3)

式中：f为抗剪断摩擦系数；C为黏聚力，MPa；σni为潜在滑动面某单元法向应力，MPa；τi为潜在滑动面某单元剪应力，MPa；Ai为潜在滑动面某单元面积，m2。

因此，通过对堵头及围岩进行有限元模拟计算，可得到堵头与围岩接触面上的法向应力和剪应力，从而选取堵头的抗滑极限状态来对堵头可靠性进行研究分析。

2 导流洞堵头可靠性功能函数的建立及可靠性分析

2.1 导流洞堵头可靠性功能函数

利用非线性有限元分析软件ABAQUS建立水工隧洞堵头及围岩的三维有限元计算模型，在可靠性理论的基础上建立堵头力学性能可靠性的显式功能函数。结合堵头可靠性功能函数的特点选择合适的可靠度计算方法，利用MATLAB编制可靠度计算程序计算出堵头可靠指标及失效概率。

参考某水利枢纽导流洞堵头设计工程参数进行有限元模拟，计算模型如图1。

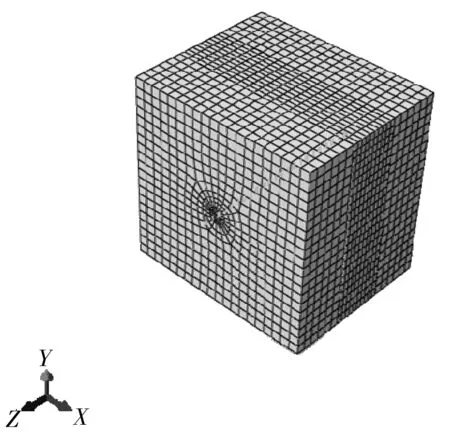
图1 堵头和围岩有限元计算模型Fig. 1 The finite element model of the plug and surrounding rocks

圆形隧洞直径为10 m，设计水头为100 m，并且在整个计算过程中假设作用水头恒定，堵头位于Ⅳ类围岩段；堵头总长度30 m，以C25混凝土浇筑堵头，其上游端与下游端嵌入围岩的深度分别为1.5、0.5 m。围岩范围横截面选取堵头边界外50 m，长度取60 m。模型顶部自由，按 2.71 MPa的自重应力施加竖向荷载，模型左右两侧和上下游侧围岩边界以及底部围岩边界分别施加法向约束，堵头上游断面施加1 MPa水压力，堵头下游断面处于临空状态。

以围岩的黏聚力C、内摩擦角φ、弹性模量E作为基本随机变量，令某一随机变量取不同的参数值而其他随机变量都取定值，利用ABAQUS有限元模型分别计算出堵头与围岩接触面的摩擦力，拟合出摩擦力关于不同随机变量的单一变化函数。在此基础上，通过多元素回归分析，最终得到摩擦力关于这些随机变量的整体显示表达式。

对于Ⅳ级围岩，参照相关资料，得到随机变量的统计特征为表1。改变模型中围岩材料参数，对模型进行分析计算，当其中一个随机变量取变值时，其它变量均取最小值。各随机变量取值如表2。

表1 随机变量统计特征Table 1 The statistical characteristics of random variables

表2 随机变量取值Table 2 The random variable values

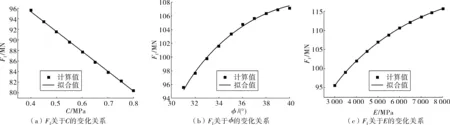
图2 单一因素作用下接触面摩擦力的变化Fig. 2 The friction of the contact surface changed with the single factor

经过ABAQUS计算分析，可以得到堵头与围岩接触面上的径向压应力，乘上相应的接触面积，并沿接触面积分即得总法向力，那么可以得到接触面的摩擦力为

Ff=∑σniAif

(4)

式中：f为抗剪断摩擦系数。

计算可得各随机变量在单因素变化下的摩擦力，通过ORIJIN8.0对计算结果进行拟合，如图2，可以得到摩擦力关于各随机变量的函数表达式。

Ff关于C的函数为

Ff=131.799-42.968C

(5)

相关指数R2=0.984；

Ff关于φ的函数为

Ff=142.525-448.583e-0.087 94φ

(6)

相关指数R2=0.999；

Ff关于E的函数为

Ff=144.603-68.809e-0.000 263E

(7)

相关指数R2=1。

在得出堵头与围岩接触面摩擦力与各随机变量在单因素变化下的函数关系式后，再进一步通过多元素回归分析求出摩擦力关于3个随机变量的多因素函数关系：

Ff=188.197-39.897C+426.409e-0.087 9φ-67.402e-0.000 263E

(8)

相关指数R2=0.998。

根据前面得到的堵头可靠性功能函数式(2)，可得堵头功能函数显式表达式：

g=55.465+1 088.628C+426.409e-0.087 9φ-67.402e-0.000 263E

(9)

2.2 堵头可靠度指标计算

现阶段，用以计算可靠度的常用方法有一次二阶矩法、二次二阶矩法、渐进积分法、响应面法、蒙特卡洛法等多种计算方法[1]。对比分析几种常用的可靠度计算方法的适用条件和优缺点可知，在具体应用中，主要是根据功能函数是否为线性和其中基本随机变量不同的概率分布类型来选用合适的计算方法。

选取对水工隧洞堵头的设计影响较大的3个因素，即围岩黏聚力、内摩擦角、弹性模量作为基本随机变量，并假定这3个随机变量均独立且服从正态分布，通过ABAQUS有限元计算分析可以得到水工隧洞堵头结构功能函数的显示表达式，选用设计验算点法进行可靠度的计算。根据设计验算点法计算原理，编制了计算堵头可靠度的MATLAB程序，若以Pf表示水工隧洞堵头的失效概率，β为堵头可靠度，二者关系可由Pf=1-Φ(β)表示。由此可知，在计算失效概率时，可通过求解其可靠度来实现。运行计算程序，可计算得到该堵头的可靠指标β=6.602 7，失效概率Pf=2.018 5×10-11。

3 水工隧洞堵头设计参数优化

3.1 目标可靠指标分析

在结构设计时，如何考量其可靠程度，或如何确保此结构设计合理有效，存在一些最低标准，其中目标可靠指标(β0)即是在可靠度中的最低标准。表3为我国建筑工程、港口工程、公路工程和水利水电工程结构可靠度设计标准[13-15]。

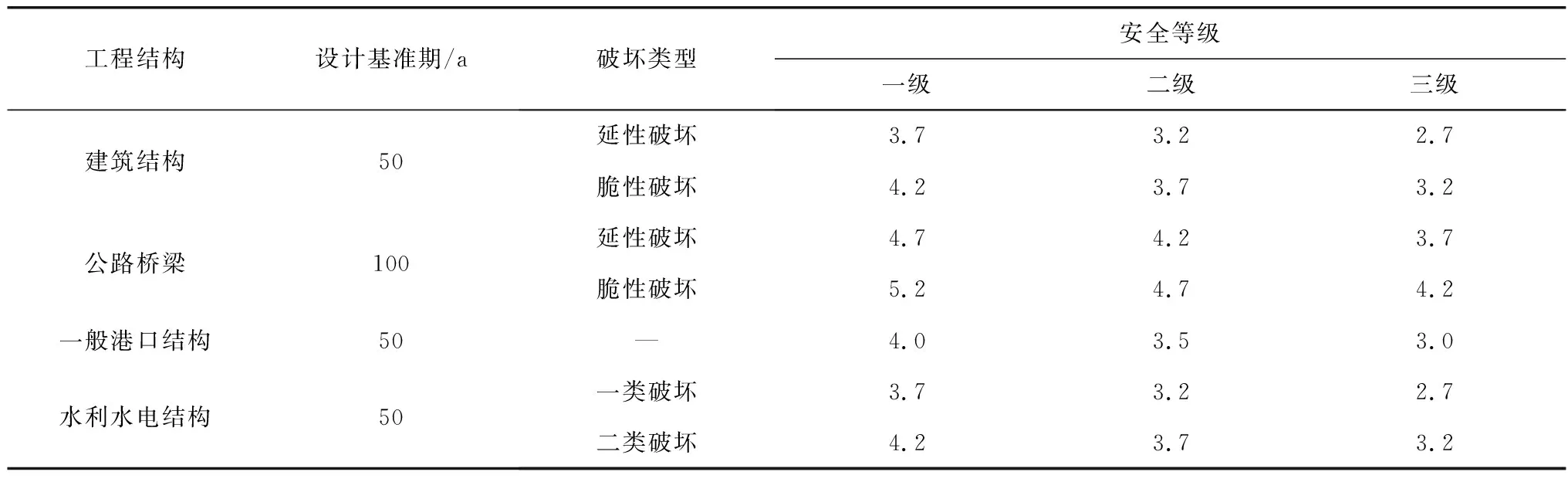
表3 我国工程结构承载能力极限状态设计的目标可靠度Table 3 The target reliability of the load capacity limiting state of Chinese engineering structure

按照校准法确定的各结构承载能力极限状态设计的目标可靠指标，考虑了结构的破坏类型和安全等级，脆性破坏构件的可靠指标要比延性破坏构件高0.5。实际对于两相邻安全等级的构件而言，其可靠性指标的差值较小。但是据此计算出的失效概率却相差甚大，有大概一个数量级之差。

国际标准ISO 2394：1998《结构可靠性总原则》给出了目标可靠指标的示意值，如表4，可靠性指标是根据抗力服从对数或威布尔分布、永久作用服从正态分布和可变作用服从极值Ⅰ型分布确定的。该标准的建议是：

1)A使用极限状态：采用βT=0；对于不可逆的使用极限状态，采用βT=1.5。

2)B疲劳极限状态：取决于检验的可能性，采用βT=2.3～3.1。

3)C承载能力极限状态：采用βT=3.1、3.8和4.3。

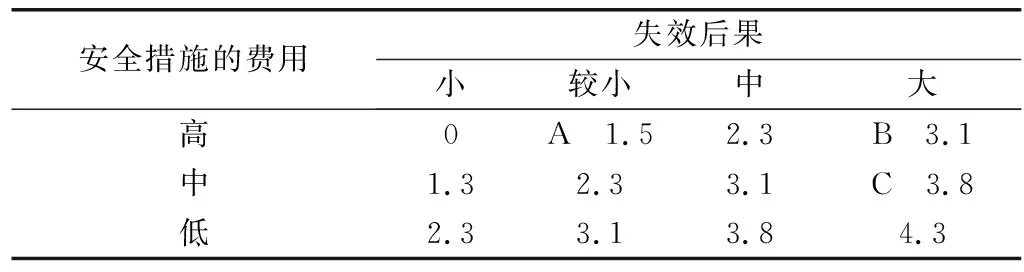
表4 ISO 2394的目标可靠指标的示意Table 4 The reliable targets of ISO 2394

3.2 不同长度堵头可靠度计算

参照以上标准，根据上述堵头的可靠度计算结果，30 m长度的堵头趋于保守，不仅延长了工期，而且还增加了工程造价，造成不必要的浪费。所以需要找到一个合适的堵头长度，既满足可靠性要求而又经济合理。因此，改变堵头的长度，分别计算不同长度下堵头的可靠性，进而找到一个最合适的长度值。将堵头模型长度分别改为10、15、20、25 m，其它条件不变，依次对模型进行分析计算，得出各个长度堵头的可靠指标及失效概率，计算结果如表5。

表5 不同长度堵头的可靠指标及失效概率Table 5 The reliable index and failure probability of the plug with different length

3.3 堵头抗滑稳定性分析

在上述研究堵头可靠性的有限元计算分析中提取出围岩C、φ、E都取均值时的计算结果，能够得出沿接触面的摩擦力Nf，黏结有效面积系数取0.6，水压力为作用于堵头上的唯一外荷载，故水平方向合力为堵头上游面的水压力，据此可以对堵头稳定性进行计算分析。利用混凝土重力坝抗滑稳定安全系数计算方法，即式(10)计算不同长度堵头相应的抗滑稳定安全系数K。

(10)

式中：[K]为允许安全系数；K为抗剪断安全系数；N为滑动面法向力，MN；f为抗剪断摩擦系数；α为黏结有效面积系数；A为有效承剪面面积，m2；C为黏聚力，MPa；∑PH为水平方向合力，MN。

计算出各长度堵头的抗滑稳定安全系数K如表6。

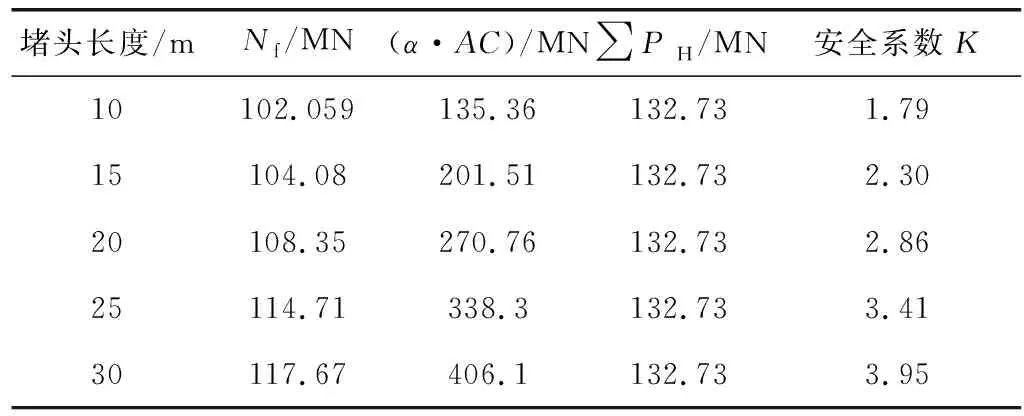
表6 不同长度堵头的抗滑稳定安全系数Table 6 The anti-sliding stability safety factor of the plug withdifferent lengths

如按照《混凝土重力坝设计规范》的规定，堵头长期运行时，永久堵头在设计荷载的作用下K≥3，故只有25 m、30 m长度的堵头才满足稳定性要求。

3.4 基于可靠性的堵头设计长度优化分析

从表5中数据可知，20 m长度的堵头已具有较小的失效概率，可靠度较高，而从堵头的抗滑稳定安全系数来看，20 m堵头并不符合稳定性要求，考虑到采用重力坝抗滑稳定安全系数核算方法来计算堵头的稳定性时，没有考虑水压力作用下堵头受围岩的侧向约束的有利影响，计算比较保守，因此笔者根据对不同长度堵头可靠性的分析研究得出的结果，并结合我国标准和国际标准中的结构可靠指标建议值，认为20 m长度的堵头是安全合理的。

4 结 论

将可靠性理论引入到水工隧洞堵头的设计计算中，建立基于可靠性理论的堵头设计参数优化分析方法。

1)通过对导流洞堵头极限状态的分析，建立极限状态方程，并在此基础上，利用非线性有限元分析软件ABAQUS建立导流洞堵头及围岩的三维有限元计算模型，在可靠性理论的基础上建立堵头力学性能可靠性的显式功能函数，选用设计验算点法编制了计算堵头可靠度的MATLAB程序，计算出设计堵头的可靠指标为β=6.602 7，失效概率为Pf=2.018 5×10-11。

2)分析了国内外工程结构可靠性指标标准，在此基础上，针对该水工隧洞，分别对长度为10、15、20、25 m堵头模型进行可靠性分析计算得到可靠指标分别为4.15、5.04、5.7、5.9；再对各长度的堵头进行稳定性分析，得到相应的抗滑稳定安全系数K分别为2.3、2.86、3.41、3.95。综合考虑堵头应满足的可靠性和稳定性要求，认为可将堵头长度从30 m优化为20 m。