地铁行车荷载作用下粉质黏土累积孔压特性研究
2019-05-13赵中华
赵中华,雷 勇
(1.沈阳城市建设学院 土木工程系, 辽宁 沈阳 110167;2.中国建筑材料工业地质勘查中心辽宁总队, 辽宁 沈阳 110004)
近几年,地铁工程的大量建设引发的工程环境问题较多[1-3]。地铁在运营期间,隧道周围土体的孔隙水压力会不断发生变化,进而影响了土体的力学性能发生改变。因此,研究地铁行车荷载作用下土体的孔隙水压力变化规律就显得极为重要。
目前,一些学者就地铁行车荷载作用下土体孔隙水压力变化规律进行了深入研究。宫全美等[4]对地铁隧道地基土中孔隙水压力的变化进行了研究,研究发现:在低频范围内孔隙水压力变化较小,频率越高,产生的孔隙水压力越大。周念清[5]通过对上海地铁某区间隧道进行监测,结果发现:地铁行车荷载引起的孔隙水压力,其消散过程需要的时间要比增加过程需要的时间多得多。王明飞[6]基于ANSYS有限元软件,研究地铁隧道周围饱和粉土的孔隙水压力发展规律,研究表明随着地铁列车运行速度的增加,饱和粉土的孔隙水压力逐渐降低。王元东[7]对地铁隧道周围加固软黏土进行了循环三轴试验,试验表明在其他条件相同时,随着荷载幅值和振动次数的增加,孔隙水压力也相应增加,随着围压和频率的增加,孔隙水压力反而减小。魏新江[8]对杭州地区饱和软黏土进行了循环三轴试验,试验表明固结程度越高的土体,孔压发展越慢。葛世平[9]通过监测发现:随着深度的增加,孔隙水压力先增加后减小,在拱腰周围产生的孔隙水压力最大。黄强[10]基于有限元软件,对上海地铁某区间隧道下卧层超孔隙水压力进行了分析,结果表明随着离隧道中心距离的增加,水平断面上超孔隙水压力不断衰减,越接近隧道断面,衰减越快,纵断面隧道正下方产生的超孔隙水压力随深度增加而减小。谢兵乐[11]采用动态空心圆柱测试系统,对天津滨海地区饱和软黏土的孔隙水压力发展规律进行了研究,研究表明随着围压、荷载幅值及振动次数的增加,孔隙水压力逐渐增大,而随着频率的增加,孔隙水压力反而逐渐降低。丁智[12]基于室内动三轴试验,对杭州地区原状淤泥质黏土的孔压特性进行了研究,研究表明初始固结度对孔压发展有较大的影响,固结度越低,峰值孔压越大,稳定后的孔压也越大。丰土根等[13]研究振动频率对饱和松砂影响时发现:频率越高,饱和松砂达到峰值孔压所需振动次数越多。逯鹏宇等[14]对武汉地铁隧道周围软黏土和砂土的孔隙水压进行了研究,研究表明循环荷载作用下,孔隙水压经历了快速增长、匀速增长和衰减稳定3个阶段。田飞等[15]基于有限元软件,对交通荷载的特性进行了研究,研究表明交通荷载可简化为一种带参数的正弦公式。
以上学者基于现场监测、室内试验和有限元模拟,研究了不同因素对孔隙水压力的影响,虽然得到了一些研究成果,但某一些结论也并不一致,比如频率对孔隙水压力的影响。由于土体具有极大的结构性和空间变异性,不同地区土体的特性不同,因此有待进一步研究沈阳地区地铁行车荷载作用下粉质黏土孔隙水压力特性。
1 室内GDS试验
本试验土样选取沈阳地铁九号线某站附近基坑坑内,为减小在取土过程中土体被扰动以及离散性所带来的试验误差,本次取土采用人工取土方式。土的基本物理性质指标如表1所示,动三轴试验方案如表2所示。

表1 土的基本物理性质指标

表2 试验方案
2 试验结果分析
2.1 围压对累积孔压的影响
图1为不同围压试验条件下累积孔压与振动次数的关系曲线,从图1中可以看出,在振动初始阶段,累积孔压表现为迅速增长趋势,随着振动次数的增加,累积孔压曲线发生明显的转折,增长的速率虽然有所减缓,但是增长的绝对值仍然较大。经过一段时间积累后,累积孔压出现两种不同的发展趋势,一种是进入稳定增长阶段,累积孔压不再随着振动次数的增加而增长,此时的累积孔压已经达到极限值,如A2试样所示;另一种是继续随着振动次数的增加而增长,但是增长的速率逐渐减小,如A6试样所示。
从整体发展趋势来看,累积孔压增长趋势大致经历三个阶段:第一阶段发生在振动次数为0~500之间,此阶段的累积孔压呈线性增长趋势;第二阶段发生在振动次数为500~2 000之间,此阶段的累积孔压呈指数型增长趋势;第三阶段发生在振动次数为2 000~10 000之间,此阶段的累积孔压呈稳定型增长趋势。

图1不同围压下累积孔压与振动次数的关系曲线
从图1中还可以看出,在相同试验条件下,围压越大,地铁行车荷载作用下土体产生的累积孔压越小。这是因为在相同的固结应力比条件下,围压越大,土体受到的轴向压力越大,在固结过程中土体被压得较密实,导致孔隙水压力排水通道越来越小,故土体产生的累积孔压就越小。这也充分表明,在地铁隧道垂直方向内,土体越深,孔隙水压力越难以发展。
2.2 固结比对累积孔压的影响
图2为不同固结比试验条件下累积孔压与振动次数的关系曲线,从图2中可以看出,在地铁行车荷载作用下,土体产生的累积孔压随着固结比的增大而减小。这主要是因为在相同的试验条件下,固结比越大,在围压相同的情况下,土体的轴向应力越大,土体在固结过程中越容易被压密,导致孔隙水压力排水通道越来越小,所以在相同的动应力幅值和频率作用下,累积孔压就难以上升。
通过整理数据发现,累积孔压达到极限值时,固结比为1.0时产生的累积孔压占有效围压23.8%,固结比为1.5时产生的累积孔压占有效围压17.9%,固结比为2.0时产生的累积孔压占有效围压11.5%。由此可知,随着固结比的增加,土体的累积孔压比(即孔压/有效围压)呈线性减小趋势。
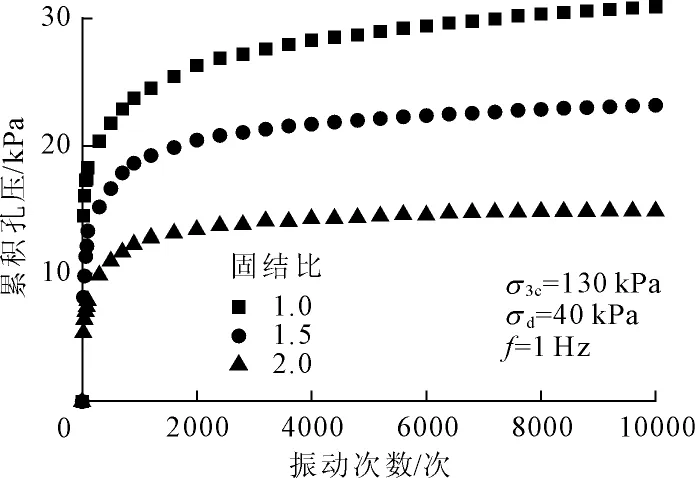
图2不同固结比下累积孔压与振动次数的关系曲线
2.3 动应力幅值对累积孔压的影响
图3为不同动应力幅值试验条件下累积孔压与振动次数的关系曲线,从图3中可以看出,随着振动次数的增加,粉质黏土的累积孔压随着动应力幅值的增加而增大。这主要是因为在相同的试验条件下,动应力幅值越大,地铁行车荷载的能量越大,由于土体的孔隙水压力要比土颗粒骨架敏感,孔隙水压力首先吸收地铁振动荷载传来的能量,与此同时土体的有效应力减小,导致土单元薄弱连接处发生松动,形成微裂缝,随着振动次数的增加,微裂缝逐渐被贯通,形成连通的孔隙水压力通道,致使孔隙水压力上升。
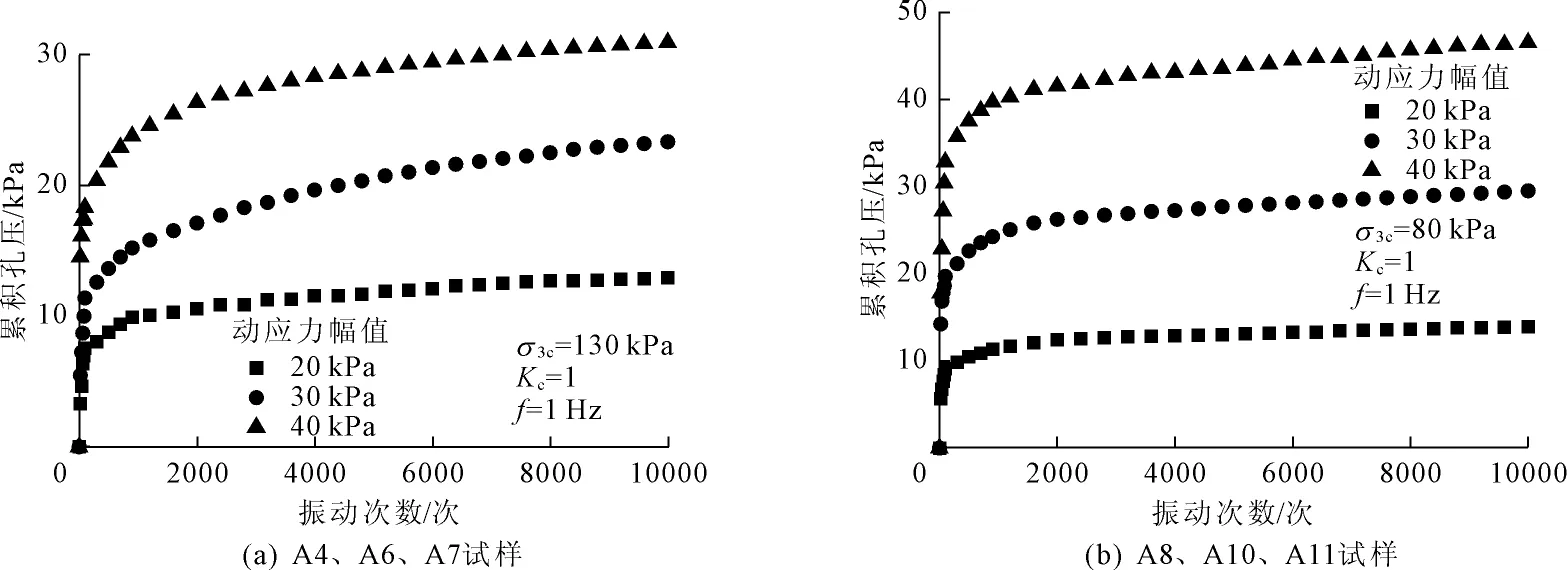
图3不同动应力幅值下累积孔压与振动次数的关系曲线
从图3还可以看出,粉质黏土的累积孔压随动应力幅值的增加而增大的幅值有所不同。当围压为80 kPa时,动应力幅值每增加10 kPa,累积孔压增加15.6 kPa~17.1 kPa;当围压为130 kPa,动应力幅值每增加10 kPa,累积孔压增加7.6 kPa~10.4 kPa。由此可见,在低围压试验条件下累积孔压随动应力幅值的增加而增大的幅值较高围压条件下要明显。
2.4 频率对累积孔压的影响
图4为不同频率试验条件下累积孔压与振动次数的关系曲线,从图4中可以看出,粉质黏土的累积孔压发展趋势表现一致。在振动初始阶段,由于土体中孔隙水压力吸收了大部分能量,使孔隙水压力瞬间上升,随着振动次数的增加,土体越来越密实,孔隙水压力的上升速率明显较振动初期缓慢,随着振动次数的继续增加,孔隙水压力不再上升而是处于稳定状态保持不变。
从图4还可以看出,累积孔压随着频率的增大而减小,这是因为频率越低,孔隙水压力有足够的时间来吸收能量,从而使孔隙水压力上升幅度越大。通过整理数据发现,当围压为80 kPa时,0.5 Hz频率下产生的累积孔压分别是1 Hz和2 Hz的1.2和1.5倍;当围压为130 kPa时,0.5 Hz频率下产生的累积孔压分别是1 Hz和2 Hz的1.3和2.1倍。由此可见,在地铁设计时,要以低频荷载作为参考指标,这将为地铁正常运营提供可靠依据。

图4不同频率下累积孔压与振动次数的关系曲线
2.5 振动次数对累积孔压的影响
图5为不同振动次数下累积孔压变化曲线图,从图5中可以看出,在四种不同试验条件下,累积孔压的增长速率均随着振动次数的增加而逐渐减小。这是因为随着振动次数的增加,土体越来越密实,孔隙水压力通道越来越小,孔隙水压力的累积速率越来越弱,导致孔隙水压力的上升幅值越来越低。
通过整理数据发现,当围压为80 kPa、130 kPa、180 kPa时,振动次数为2 000次产生的累积孔压分别占极限孔压的89%、73%、79%;当固结比为1.0、1.5、2.0时,振动次数为2 000次产生的累积孔压分别占极限孔压的82%、73%、85%;当动应力幅值为20 kPa、30 kPa、40 kPa时,振动次数为2 000次产生的累积孔压分别占极限孔压的90%、85%、86%;当频率为0.5 Hz、1.0 Hz、2.0 Hz时,振动次数为2 000次产生的累积孔压分别占极限孔压的85%、88%、90%。
从以上述数据分析发现,围压越小,振动初始阶段所产生的累积孔压占极限孔压的比值较大,而对于固结比、动应力幅值以及频率因素来说,振动初始阶段所产生的累积孔压占极限孔压的百分比受因素水平的影响并未形成一致的规律。比如频率为0.5 Hz和2.0 Hz时,振动次数为2 000次产生的累积孔压分别占极限孔压的85%和90%,从数据上来看,频率为2.0 Hz时产生的效果更明显,这显然与“低频荷载作用产生的累积孔压比高频荷载作用效果显著”结论似乎并不一致。本文仔细研究发现,之所以出现这种现象的原因:其一是因为土体本身的结构存在差异所带来的试验结果,其二可能由于频率和振动次数因素之间存在耦合作用,在一定程度上对累积孔压的变化产生影响。但总体来说,在相同试验条件下,低频荷载作用产生的累积孔压远远要比高频荷载作用产生的累积孔压大。
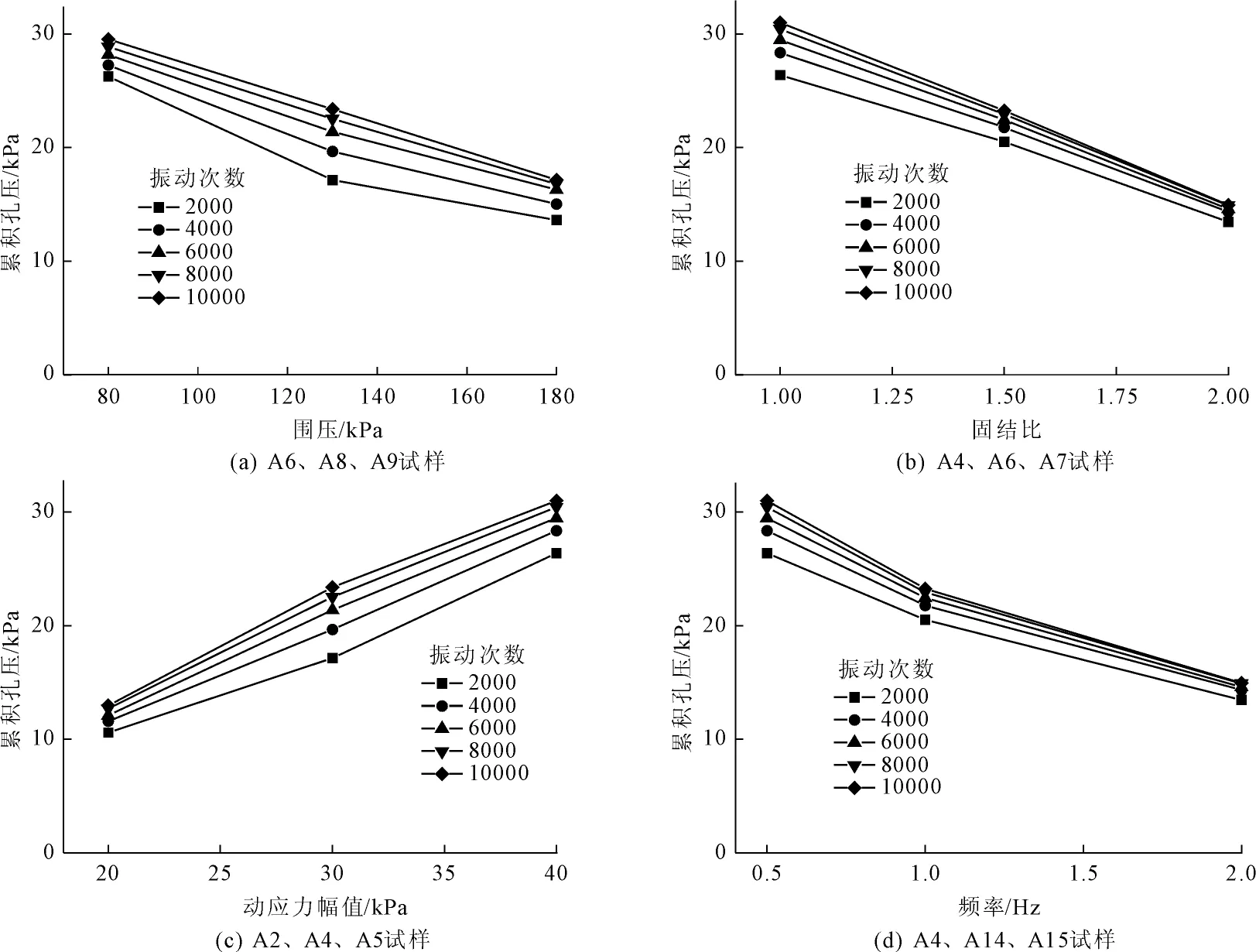
图5不同振动次数下累积孔压变化曲线
3 结 论
(1) 在相同试验条件下,累积孔压随围压增大而减小,随固结比增大而减小,随动应力幅值增大而增大,随频率增大而减小,随振动次数增大而增大。
(2) 在低围压试验条件下,累积孔压随动应力幅值的增加而增大的幅值较高围压条件下要明显。
(3) 在四种不同试验条件下,累积孔压增长率随振动次数的增加而变化的规律一致,即随着振动次数的增加,累积孔压增长率逐渐减小。
