BP神经网络在水下地形高程拟合的应用

彭中波， 高 阳

重庆交通大学 航运与船舶工程学院，重庆 400041)

0 引 言

人工神经网络是模仿人类大脑的结构和功能的一种信息处理系统[1-2]，由于具有并行结构和并行处理能力、知识能够分布式存储、良好的容错性以及自适应学习能力等特点，在信号处理、模式识别、智能检测以及人工智能等领域得到广泛应用。具有3层或3层以上结构的无反馈、层内无互联结构的前向神经网络，即为BP神经网络。它采用有指导的学习方式进行训练和学习，即在一给出的BP神经网络中，输入神经元的激活值从输入层经过各个隐含层传递到输出层，在输出层的各个神经元得到神经网络的实际输出。对神经网络的实际输出与期望输出值进行比较，得到输出值的误差，再逐层修正各个从输出层至隐含层的连接权值，最后返回到输入层并不断重复该过程，使误差值减小到能够接受的范围。

随着市政工程的不断发展完善，高程测量[3-5]工作显得尤为重要，测量值的准确性将直接影响到工程的质量。在市政工程中高程的主要测量方式有GPS技术测量、水准测量、三角高程测量和气压高程测量[6-9]，其中以GPS技术测量、水准测量两种方式所测数据最为精密，但是整个测量过程中对设备及设备的安装位置有特定的要求，测量步骤也较为复杂，都需要严格按照相关测量规范进行。针对乌江河口至白马河段水下地形图高程测量问题，利用MATLAB提供的神经网络函数编程实现GPS正常高的神经网络数据拟合[10-12]。

1 BP神经网络模型与理论基础

BP(Back Propagation)神经网络是一种典型的多层前向型网络，可以实现从输入到输出的任意非线性映射。网络中通常含有一个或多个隐含层，各个神经元接受前级输入并输出到后级，最终网络的输出是由输入与其对应的权值求取加权和后通过传递函数得出。BP网络的输出可以通过选择最后一层的传递函数确定。传递函数为S型时，输出量为0～1的连续量；传递函数是线性传递函数时，网络输出量可以取任意值。其中隐含层神经元采用S型传递函数，输出层神经元采用线性传递函数。BP神经元模型如图1。

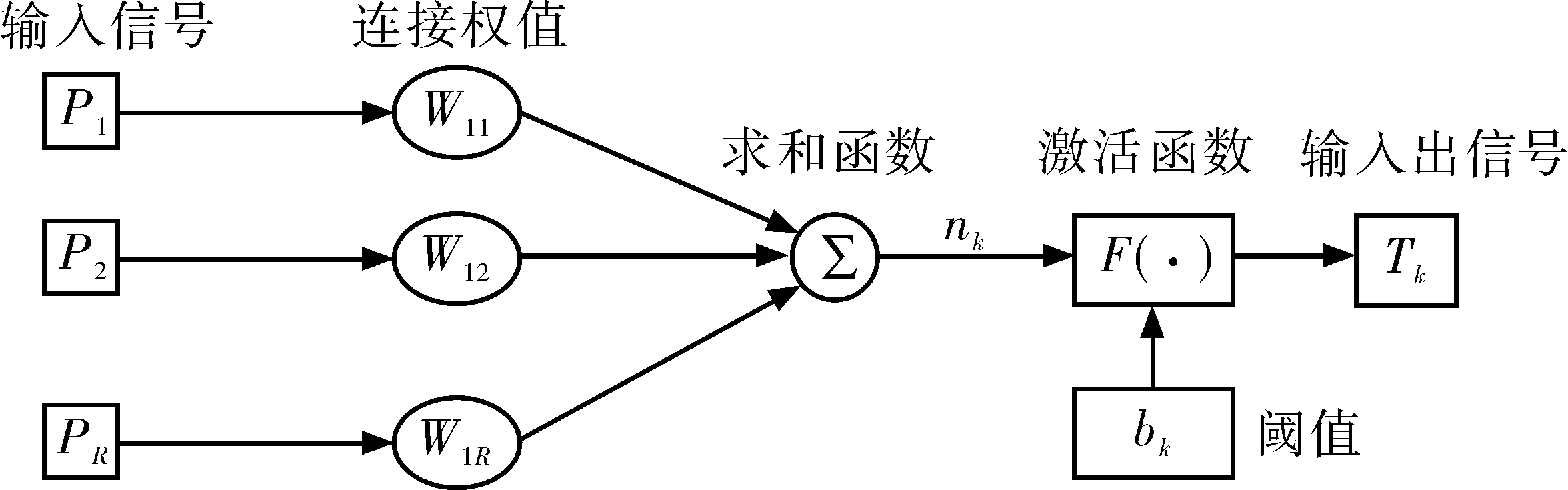
图1 BP神经元模型Fig. 1 BP neuron model

图1是具有R个输入的神经网络模型。每一个输入信号的连接强度都用一权值表示，权值的刺激或者抑制作用通过对权值取正负值表示。给输入信号相应突触加权之和添加一个阈值，根据阈值的正负值去增加或减少激活函数的输入。激活函数主要作用是限制神经元的输出振幅，将输入信号限制在允许范围之内。一般的输出的幅度范围有[0,1]和[-1,+1]两种。

BP神经网络输入输出之间的线性或非线性关系都可以由隐含层的非线性传递函数神经元学习拟合获得，输出层采用线性传递函数是为了拓宽网络输出。图2为一典型BP网络结构，含有一个神经元数目为s的隐含层，隐层神经元传递函数tansig，输出层神经元传递函数purelin[13]。

图2 BP网络结构Fig. 2 BP network structure

2 BP神经网络设计

2.1 神经网络问题简述

将以获取点的坐标值(xi，yi)和相对应的高程值zi作为新建神经网络的数据样本：

P={P1,P2,P3,…,Pn}

(1)

式中：Pi=(xi,yi,zi)，i=1,2,3,…,n。

对数据样本进行学习，建立映射关系：

z=f(x,y)

(2)

式中：x，y为平面坐标；z为高程值。

2.2 神经网络设计

2.2.1 样本数据的处理

从工程河段实测水下地形图中提取坐标点(x,y)及高程值z，其中坐标点作为神经网络的输入层，坐标组成向量为二维，因此输入层有两个神经元；高程值组成向量Z作为神经网络的输出层，即输出层有一个神经元。从实测图中提取的数据显示所测坐标点及高程值之间的差值较大，为了方便后面的数据处理与加快MATLAB中神经网络程序的运行及网络收敛速度，需要对样本数据进行归一化处理，归一化后的数据将分布在区间[0,1]，网络训练结束后可以将数据反归一化到原始数据的范围[14]。使用的归一化函数：

(3)

式中：P为输入输出向量P(x，y，z)；min(P)、max(P)分别为向量P(x，y，z)的最小值和最大值。

2.2.2 隐层神经元数选取

BP神经网络的神经元个数选择是关键。根据BP神经网络任意逼近定理，对于有界区域中的任意连续函数在足够多的神经元数时，都能用3层前向神经网络以任意精度逼近[15-16]。但是神经元数目较多时，神经网络训练学习的时间较长，网络复杂度增加，容错性差以及过拟合现象出现；神经元数目较少时，网络对样本数据的训练能力和预测能力不够，不能识别之前没看到过的数据，导致神经网络训练的结果达不到应用的要求。确定神经元数目的研究结果较多，笔者参考以下3个公式：

(4)

m=log2n

(5)

(6)

式中：m为隐含层神经元数；n为输入层神经元数；l为输出层神经元数；α为1～10之间的常数。

2.2.3 权值和阈值训练过程

BP神经网络的训练就是输入样本训练数据刺激网络的连接权值动态调整[17]，判断网络输出和期望输出相符精度是否符合要求，不满足的误差将反向传输进行动态修正连接权值，根据误差值对权值的偏导数的正负判断实际输出与期望输出的大小，确定权值的调整方向，使得实际与期望的误差值收敛。权值和阈值初始化即是给各连接权值赋(-1,1)区间的任一随机数，其初始化函数调用格式为：net=init(net)。网络中各连接权值和阈值矩阵根据输入层、隐层及输出层节点数确定。BP网络训练完成，权值和阈值读取函数分别为net.iw{1,1}、net.lw{2,1}、net.b{1}、net.b{2}。为了方便训练好后的网络使用，需要save net(保存网络)，在使用时只需要load net(保存网络)就能进行高程点预测。

2.2.4 传递函数及训练函数选取

1)传递函数选取

传递函数是BP网络的重要组成部分。BP网络的传递函数有多种，常用的有S型的对数或正切函数和线性函数。logsig函数也叫S型的对数函数，可取任意值为输入值，输出值为0～1之间的数；tansig函数又叫双曲正切S型传递函数，输入值可取任意数，输出值在[-1，+1]之间；线性传递函数purelin的输入值与输出值都可取任意数[18]。在实际训练中，可根据样本数据的训练误差大小选取隐层和输出层传递函数。

2)训练函数选取

在BP网络训练时，采用不同的训练函数对网络的性能影响不同[19]。BP网络主要的训练函数有Newton算法的trainbfg函数、trainoss函数；共轭梯度算法的traincfg函数、trainscg函数以及trainrp函数、trainlm函数。这些函数在计算速度、收敛速度、内存要求及误差范围等方面有各自的优缺点。因样本数据较多，需要的训练精度较高，综合各种条件选取trainlm训练函数。

3 MATLAB实现神经网络高程拟合

3.1 乌江河口至白马河段航道建设工程图

图3 工程河段航标配布及高程Fig. 3 Standard layout and elevation map of river reach

图4 局部高程点位概略分布Fig. 4 Local elevation general distribution map

3.2 乌江河口至白马河段高程值预测

该河段工程测量点较多，所获取的训练样本数据较充足。取3 000组数据作为样本数据，其中前2 000组数据作为训练数据(training data)，剩下400组作为验证数据(validation data)，600组作为测试数据(testing data)。在实验中，BP网络创建函数为newff，其函数选用及训练参数确定如表1、表2。

表1 BP网络函数选用Table 1 Selection of BP network function

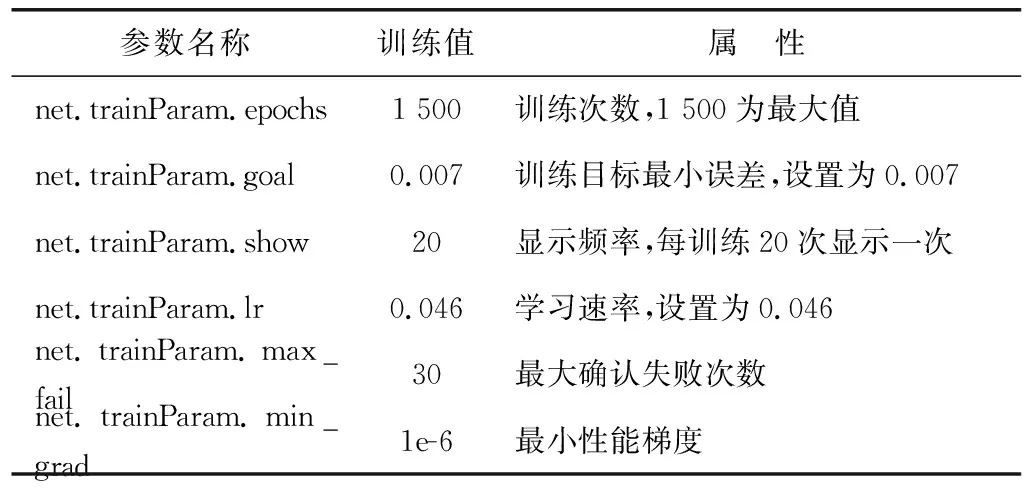
表2 BP网络训练参数Table 2 Training parameters of BP network

表1的函数选取都是针对研究河段获取的样本数据特点进行分析选取。表2中参数都是经过多次训练得出，通过以上参数训练获得的BP网络有较好的预测效果，其预测结果如图5。

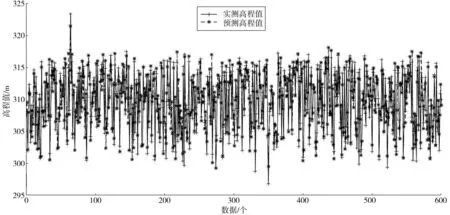
图5 河口至白马河段高程预测Fig. 5 Elevation forecast map between estuary and White Horse River reach

神经网络性能的主要参数是均方差(Mean Squared Error)，表现数据的变化程度，差值越小，拟合精度越高。拟合过程中最优的性能参数(Best Validation Performance)经过801次迭代运算得出为0.007 23，说明该预测模型拟合数据具有较高精确度。训练样本(train sample)、验证样本(validation sample)及测试样本(test sample)的均方差拟合曲线如图6。

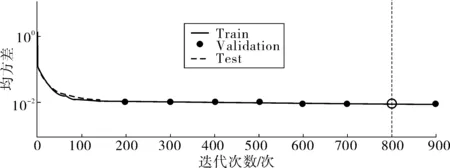
图6 训练样本、验证样本、测试样本均方差曲线Fig. 6 Mean square errer curves of train semple, validation sampleand test sample

样本数据集拟合曲线一般有线性和指数两种形式。笔者将样本数据归一化处理，采用线性拟合描述训练样本(train sample)、验证样本(validation sample)、测试样本(test sample)及整体样本分析。拟合系数R是说明神经网络训练情况，越接近1训练程度越好，更适合工程中高程预测应用。训练样本、验证样本、测试样本及整体样本拟合系数R分别为0.970 03，0.955 83，0.959 68，0.967 91，均大于0.95，其中训练样本R=0.970 03，如图7，说明该网络训练较为成功，可用于数据预测。

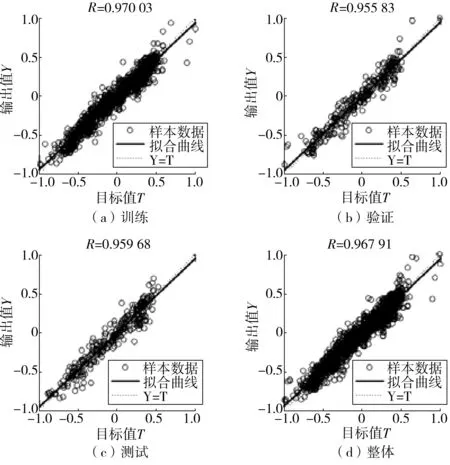
图7 训练样本、验证样本、测试样本线性拟合Fig. 7 Linear fitting of train sample, validation sample and test sample

3.2 预测结果分析

将BP神经网络拟合出的结果与工程实测高程对比分析，得出测试集拟合最大误差为4.75 m。根据统计学中的置信水平(95%)对600组拟合结果进行区间估计，最大误差为2.32 m，与对应高程点的占比为0.745%，拟合效果较好，符合地形测量的工程应用要求。拟合误差及拟合精度的点位分布如图8，高程误差都在0～2.32 m之间，在1 m范围内的误差值占总数据的70.17%，误差精度都在0.745%以内，属于较高精度等级要求。

图8 拟合误差及拟合精度点位分布Fig. 8 Fitting error and fitting precision point distribution map

4 总 结

主要对重庆地区河口至白马河段坐标数据进行分析，并对样本数据建立BP神经网络，通过训练好的BP网络对该河段更多区域高程值进行预测，并对该网络进行推广到该类河段高程预测应用，以此节省传统高程测量方式需要耗费的人力和财力资源。

研究结果主要体现在两个方面：一是针对工程河段水下地形图高程的数据特征，建立BP神经网络。神经网络的创建工作包括：①分析不同网络函数的适用范围，选取合适的函数；②网络层数及神经元个数的确定；③结构参数的选取。二是对神经网络拟合的高程值与实际测量高程值进行对比分析，通过绘制工程图的点位分布图、神经网络样本数据集的拟合误差曲线、拟合回归曲线及拟合误差和拟合误差精度的点位分布图等可知该网络训练预测值与实测值之间的误差为0.745%以内，属于工程应用的误差范围，对该河段其它未通过人为测量的高程值有预测作用。得出的BP网络还可以在更多地方得以推广应用。