改进双树复小波变换和高阶累积量的齿轮箱信号降噪方法
2018-11-15陈旭阳韩振南王志坚
陈旭阳,韩振南,王志坚
(1.太原理工大学 机械与运载工程学院,太原 030024;2.中北大学 机械工程学院,太原 030051)
由于机械设备运转时采集到的振动信号普遍存在噪声干扰,因此降噪和故障特征提取成为机械故障诊断的重点和难点。准确提取故障特征,对有效地降低机械设备振动信号噪声具有非常重要的意义。
双树复小波变换(dual-tree complex wavelet decomposition,DTCWT)是传统离散小波变换的改进方法,是由KINGSBURY正式提出的[1],即用奇、偶滤波器组实现小波的分解与重构,不仅具有传统小波的时频局部化分析能力,而且有离散小波所不具备的抗频率混叠性、近似平移不变性、完全重构性、有限的数据冗余和高效的计算效率等优良性质[2-3]。
基于参数估计和小波系数之间的相关性提出的阈值选取方法,普遍缺点是难以选取合适的阈值,从而影响了实际应用[4-5]。
高阶统计量方法对多种噪声都有很好的抑制作用。它不仅对未知自相关加性噪声不敏感,抑制高斯色噪声,而且对另一类均匀对称分布的非高斯有色噪声也不敏感,因此成为非平稳、非高斯信号和非最小相位系统的主要数学分析工具[6-7]。
由于小波分解层数的多少直接影响信号的去噪效果,因此采用粒子群算法自适应选择小波的分解层数。本文提出了自适应双树复小波和高阶累积量的信号降噪方法,利用小波系数的周期性和小波系数模震荡小的特点以及高斯随机过程的高阶累积量为零的特性实现信号降噪处理。
1 基本理论
1.1 双树复小波变换
双树复小波变换采用二叉树结构的两路滤波器组进行信号的分解和重构(见图1),一树生成实部,一树生成虚部,合理设计实、虚部树低通滤波器,满足半采样延迟条件,具有近似平移不变性。两树滤波器采样频率相同,但是它们之间的延迟恰好是一个采样间隔,这样虚部树中第一层的二抽取恰好采到实部树中二抽取所丢掉的采样值。
3层双树复小波分解和重构过程,如图1所示。分解时,h0、h1为实部树低、高通滤波器,g0、g1为虚部树低、高通滤波器。重构时,h'0、h'1为实部树滤波器组,g'0、g'1为虚部树滤波器组。
小波函数表示为如下形式:
ψ(t)=ψh(t)+iψg(t) .
(1)
式中:ψh(t),ψg(t)为两个实小波;i为复数单位。
图1中,虚线上方实部树变换的小波系数和尺度系数可由式(2)、式(3)计算:

(2)
(3)
同理,下方虚部树变换的小波系数和尺度系数可由式(4)和式(5)计算:

(4)
(5)
因此,可得到双树复小波变换的小波系数和尺度系数:

(6)
(7)
最后,双树复小波变换的小波系数和尺度系数可由式(8)和(9)重构:
(8)
(9)
双树复小波变换后的重构信号可表示为:
(10)
1.2 高阶累积量
近几年的研究结果表明,大多数机械故障信号都是非高斯、非平稳、非线性过程,仅用二阶统计量很难全面描述其特性。高阶累积量对高斯噪声与对称分布噪声中的信号检测、恢复和特征增强等方面与二阶统计量相比有独特之处,特别是非平稳、非线性过程的处理。二阶累积量处理的信号,去噪不彻底。
由于旋转机械周期性的工作性质,导致了在工作过程中测试的信号呈现周期性,因而采集到的信号大多数为对称的。对于对称分布的有用的非噪声信号,其三阶累积量也会为0.但不管是对称分布还是非对称分布的非高斯信号,其四阶累积量都不为0[8].
一般地,k维随机变量(x1,x2,…,xk),其联合概率密度函数表示为f(x1,x2,…,xk),则第一联合特征函数被定义为:

(11)
对应的第二联合特征函数为:
ψ(ω1,ω2,…,ωk)=lnφ(ω1,ω2,…,ωk)=lnE{ej(ω1xx+ω2x2+…ωkxk)} .
(12)
因此,k个随机变量(x1,x2,…,xk)的r=r1+r2+…+rk阶联合矩为对第一联合特征函数求k次导数得:
(13)
同样地,k个随机变量的r阶累积量为对第二联合特征函数求k次导数得:
(14)
一组随机变量的k阶累积量可以表示为:
Ck=cum(x1,x2,…,xk) .
(15)
式中:cum()代表联合累积量。设{x(n)}为零均值的实随机过程,k阶累积量Ckx(τ1,τ2,…τk-1)定义为:
Ckx(τ1,τ2,…,τk-1)=cum{(x(n),x(n+τ1),…,x(n+τk-1))} .
(16)
实际中,可以由M-C(矩-累积量)公式直接得到一个最简单的关于高阶累积量的关系式。
二阶累积量:
C2x(τ)=E{x(n)x(n+τ)}=Rx(τ) .
(17)
三阶累积量:
C3x(τ1,τ2)=E{x(n)x(n+τ1)·x(n+τ2)}=m3x(τ1,τ2) .
(18)
四阶累积量:
C4x(τ1,τ2,τ3)=E{x(n)x(n+τ1)x(n+τ2)·x(n+τ3)}-Rx(τ1)Rx(τ2-τ3)-Rx(τ2)·Rx(τ3-τ1)-…-Rx(τ3)Rx(τ1-τ2) .
(19)
式中,Rx(τ)为{x(n)}的二阶矩,即自相关函数。如果x为高斯随机过程,则x的四阶累积量为0.
1.3 PSO算法
不同于进化类算法的复杂遗传因子的过程,粒子群优化算法采用速度-位移模式进行全局搜索优化。同时继承了人工智能的记忆特性,可以根据当前最好的那个粒子位置及时调整搜索策略,是一种高效的搜索算法[9]。
粒子群算法的思想来源于鸟群觅食的群体共享机制模拟。每个粒子都是解空间中的一个解,根据自己和同伴的经验随时改变自己的速度和位置(即层数)从而到达目标地点。每个粒子的最优解即个体极值为pb而整个群体的最优解即全局极值为gb,每个粒子都是通过pb和gb随时调整自己的位置和速度。改变位置和速度的公式为:
Vi(t+1)=ωVi(t)+c1rand(pbi-xi(t))+c2rand(gb-xi(t)) .
(20)
Xi(t+1)=xi(t)+Vi(t) .
(21)
具体步骤为:
1) 初始化各粒子的速度和位置。
2) 确定一个适应度函数,将降噪后的信噪比和降噪前信噪比差值的绝对值作为适应度函数。比较粒子个体与种群的适应度值,个体中信噪比值最大的粒子为个体最优值,种群中信噪比值最大的粒子为种群最优值。
3) 通过式(20)和式(21)更新粒子的速度和位置。i表示第i个粒子,t表示迭代次数,rand为[0,1]上的随机数,c1,c2为学习因子。种群规模t取10次,视问题的复杂程度而定;ω取0.4~1;和取1.0.
4) 计算粒子和种群的适应度函数值,通过与前一步中的个体和种群最优值进行比较,更新个体和种群最优值。判断新种群是否达到终止条件,达到则执行步骤5),否则继续执行步骤4).
5) 退出迭代,输出全局最优值(即层数)。
2 改进双树复小波变换和高阶累积量的信号去噪
2.1 理论分析
假设信号中含有未知功率密度谱的零均值高斯噪声,信号模型可以表示为:
x(k)=f(k)+n(k) .
(22)
假设xj是尺度j上的小波系数,因为小波是线性变换,而且信号相互独立,所以
xj=fj+nj.
(23)
式中,n是高斯噪声,f是信号成分。利用高斯随机过程的四阶累积量为0,则:
(24)
可以得到:
(25)
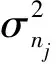
含信号成分的小波系数的四阶累积量大于0,而噪声的4类累积量等于0,因此去掉了小波系数的噪声,保留小波系数的有用信号。估计噪声方差值[7]:
(26)
在尺度j上,噪声的方差是:
(27)
其中,G是高、低通滤波器增益。
对各层小波系数进行处理时采用如下原则:
(28)
2.2 实施步骤
1) 利用粒子群算法,选择双树复小波分解最优分解层数。
2) 对含噪信号按粒子群所寻到的最优分解层数进行双树复小波分解。
3) 将各层双树复小波系数进行反变换,分别重构出各层系数。
4) 对重构后的高频小波系数进行式(27)的门限降噪处理。
5) 将降噪后的信号与传统的阈值处理双树复小波系数降噪得到的信号进行对比,得出结论。具体流程如图2所示。

图2 实施流程图Fig.2 Implementation flow chart
3 仿真及实验结果对比和分析
3.1 仿真信号分析
构造如下齿轮局部故障仿真信号验证本文方法的可行性和有效性,调幅-调频信号的表达式:
x(t)=0.2[1+cos(2π×30t)]+[1+cos(2π×30t)]×cos(2π×120t)+[1+cos(2π×30t)]×cos[2π×150t+cos(2π×5t)] .
(29)
由图3可以看出用粒子群寻优时,当分解层数为3层时所得适应度值最大。

图3 适应度值随分解层数的变化Fig.3 Fitness values varies with the number of decomposed layers
图4为纯净信号的波形图和频谱图。在以上纯净信号中加入随机白噪声,如图5所示为含噪信号波形图和频谱图。30 Hz频率被淹没在噪声中,无法识别出。
采用本文方法进行降噪处理,降噪效果如下图6所示,可以清晰地识别出各特征频率成分,降噪效果比较理想。
图7所示为用硬阈值方法降噪后的信号的波形及频谱图。从图中可以看出30 Hz的特征频率被淹没在噪声中,降噪效果不理想。
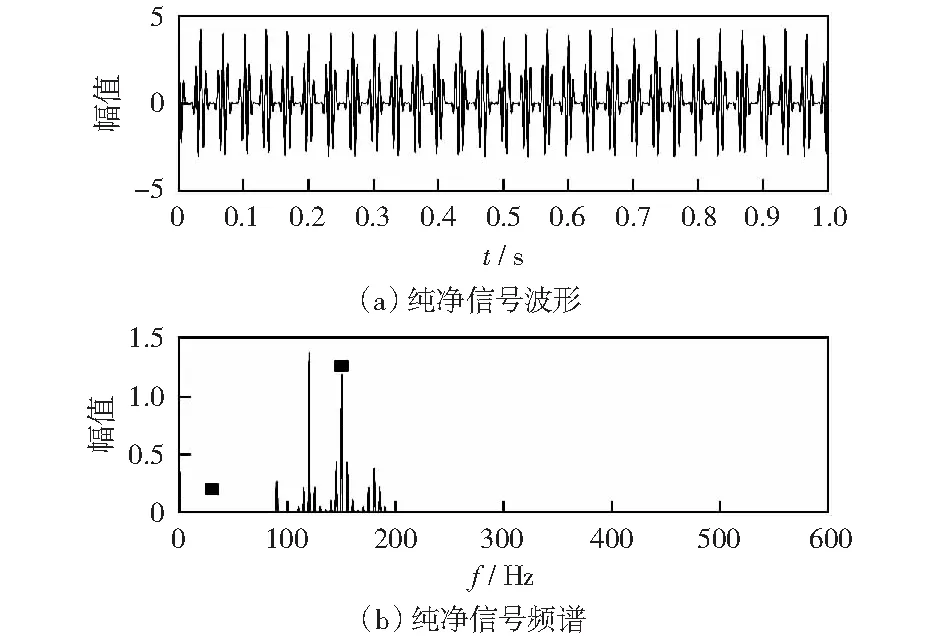
图4 纯净信号波形图及频谱图Fig.4 Pure signal waveform diagram and spectrogram

图5 含噪信号波形图及频谱图Fig.5 Noise signal waveform diagram and spectrogram
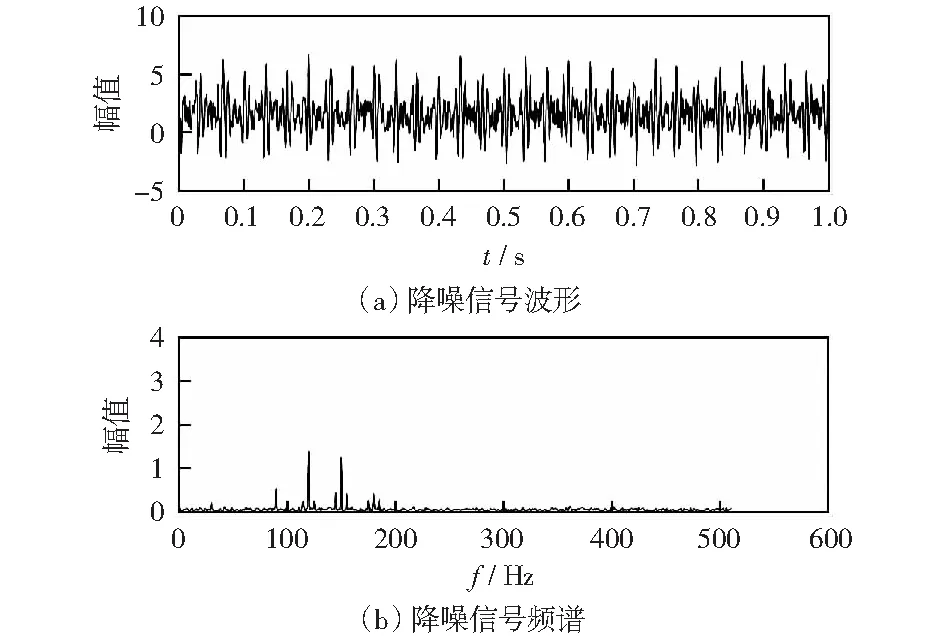
图6 本文降噪信号波形图及频谱图Fig.6 This article noise reduction signal waveform diagram and spectrogram
图8所示为用软阈值方法降噪后的信号的波形及频谱图。从图中可以看出30 Hz的特征频率被淹没在噪声中,降噪效果不理想。
通过对比从波形图中可以明显、清晰地看出经本文方法处理后的信号降噪效果比较理想且从频谱图可以识别出各特征频率成分,和软、硬阈值法相比更能有效地降低信号噪声,提高信噪比。
3.2 实验信号分析

图7 硬阈值降噪信号波形图及频谱图Fig.7 Hard threshold noise reduction signal waveform diagram and spectrogram
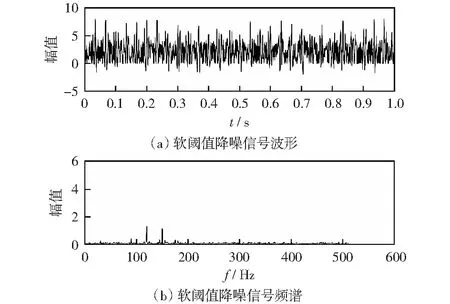
图8 软阈值降噪信号波形图及频谱图Fig.8 Soft threshold noise reduction signal waveform diagram and spectrogram
实验信号是通过齿轮疲劳强度实验台通过传感器采集到的振动信号。如图9所示,加速度传感器安装在齿轮箱端盖上,电动机转速保持在1 200 r/min左右,扭矩为800 N左右。采样点数为1 024,采样频率为1 000 Hz.试验齿轮的传动比为1∶1,采取半齿啮合。

图9 齿轮疲劳强度实验台Fig.9 Gear fatigue strength test bench
在齿轮啮合的实测振动信号中,由于在齿轮啮合过程中故障信号(齿轮点蚀)被淹没在电动机转动和散热大风扇转动等强背景噪声下,因而难以从采集到的信号中直接判断出齿轮箱是否存在故障。采用本文的降噪方法处理含噪信号,使之能够有效降噪,从而能更好地提取故障特征。图10为无故障的实验信号波形图及其频谱和包络谱图,从图中可以看出啮合频率的半频55 Hz和一倍频110 Hz处虽然比较明显,但有干扰频率存在。
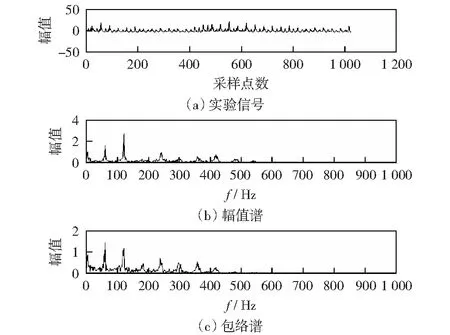
图10 无故障实验信号及其谱图Fig.10 No trouble experimental signal and its spectrum
图11为降噪后的无故障信号的波形图、频谱图和包络谱图,从包络谱图中可以看出半频和一倍频非常清晰、明显且干扰频率成分明显减少。

图11 降噪后的信号及其谱图Fig.11 Signal after noise reduction and its spectrum
图12是经过软阈值处理后的信号波形图和幅值谱、包络谱图。从包络谱和幅值谱图中可以看到在100~500 Hz之间干扰频率较多。

图12 软阈值降噪后的信号及其谱图Fig.12 Signal after soft-threshold noise reduction and its spectrum
通过图10—图12的对比,可以清晰地看到本文方法的降噪效果要优于传统的软阈值降噪方法,从两种方法的包络谱图中可以看出,本文方法比软阈值法更加有效的消除噪声信号,减少了频率干扰。
因为无法知道降噪前信号的信噪比,因此将降噪后信号的信噪比绝对值的大小作为适应度函数。选取降噪后信号信噪比绝对值的最大值所对应的小波分解层数为最优分解层数。由图13可以看出在第二层之后,降噪后信号的信噪比基本趋于平稳,因此本文选择的小波最优分解层数为3层。

图13 信噪比的大小随分解层数的变化Fig.13 Size of the signal to noise ratio varies with the number of decomposed layers
图14所示为加速度传感器安装在齿轮箱端盖上,电动机转速保持在1 200 r/min左右,扭矩为1 000 N左右。采样点数为1 024,采样频率为1 000 Hz,采集到的是有故障的实验信号。因转速控制有偏差因此计算得到的啮合频率存在偏差。
通过传感器和信号采集仪采集到的实验信号波形图以及包络谱图如图14所示。由于故障信号比较微弱,而且淹没在强背景噪声下,从幅值谱图和包络谱图中看出有边频成分和很严重的频率干扰20 Hz以及其他干扰频率成分。从信号的包络谱图中不能准确地反映出故障特征频率。

图14 故障信号波形及其频谱图Fig.14 Fault signal waveform and its spectrum
为了能更好地降低噪声干扰,诊断出故障信号,故使用本文方法进行降噪,降噪后的信号波形图和包络谱图如图15所示。从图中可以很清晰地看出半频50.55 Hz处和啮合频率107.4 Hz与正常齿轮(图12)对比发现,在半频和啮合频率周围,边频成分明显,由此可看出存在故障特征。与图14对比看出,波形清晰,干扰信号幅值有很大程度降低,干扰频率成分被消除,去噪效果明显;且与无故障图11相比边频成分明显,幅值不均一。

图15 故障信号降噪后的波形及其频谱图Fig.15 Waveform of the fault signal after noise reduction and its spectrum
4 结论
1) 将四阶累积量方法引入双树复小波变换降噪中,根据信号和噪声的统计特性进行信噪分离。取得了很好的降噪效果。
2) 因为双树复小波分解不同分解层数会影响降噪效果,分解层数少则降噪效果不理想,而分解层数太大则容易丢失有用信号。即使分解层数大,降噪效果很好,但丢失有用信号后,信噪比反而会降低。利用信噪比作为适应度函数,通过粒子群优化选择信噪比最大的分解层数。
3) 仿真信号降噪结果表明,和双树复小波变换的传统软、硬阈值法相比,该方法在不同信号和噪声水平下均能表现出良好的自适应性和降噪效果。
4) 实验信号处理结果表明,该方法能够有效抑制齿轮箱振动信号中的强背景噪声,信号处理中能更好地减少干扰频率,有效提取故障频率。
