基于PSE-ANFIS的ZPW-2000A轨道电路故障诊断方法

2018-11-15陈姝姝田慕琴宋建成

太原理工大学学报 2018年6期

陈姝姝，田慕琴，宋建成

(太原理工大学矿用智能电器技术国家地方联合工程实验室，煤矿电气设备与智能控制山西省重点实验室，太原 030024)

近年来，中国高铁发展迅速，需要保证铁路设备的安全、稳定运行。ZPW-2000A轨道电路是以铁路线路的两根钢轨作为导体，并用引接线连接信号电源和接收设备所构成的电气回路，其轨道内传输的是移频信号。由于轨道电路运营条件的复杂性，实际中发生故障的概率较大。目前，铁路部门已建成了铁路信号集中监测系统，实时监测轨道电路的电气性能和运行状态，实现了“状态修”[1]。但是铁路信号集中监测系统缺少对室外轨旁设备电特性的监测，难以全面准确地反映移频轨道电路的真实运行状态[2]。

国内外在轨道电路故障诊断方面的研究特点是：结合传感器技术、信号处理技术、人工智能及计算机技术，将故障机理分析、故障特征信号提取以及故障诊断的研究成果应用到综合系统中。TIM et al[3]通过长短期记忆(LSTM)递归神经网络来学习轨道电路的各测量信号的时空依赖关系，从而实现轨道电路的故障诊断；段成波[4]综合运用支持向量回归、灰色模型、神经网络等方法，预测轨道电路的轨出电压，依此预判轨道电路故障。然而目前仍然存在一些问题，实际导致轨道电路故障的原因很复杂，具有明显的模糊性和不确定性；轨道电路发生故障时的大量有效信息未得到有效利用。

针对以上问题，提出了通过移频信号来反映ZPW-2000A轨道电路状态的方法。将功率谱熵和幅值下降比作为故障特征量，输入到建立好的ANFIS故障诊断模型中，对轨道电路的几种典型故障进行识别诊断。以此作为铁路信号集中监测系统室外监测的补充。

1 煤矿移频信号的功率谱熵

1.1 移频信号

ZPW-2000A轨道电路内传输的信号是一种移频信号，其时域表达式为：

(1)

式中：A，fc，Δfp，g(t)，φ0分别为移频信号的振幅、载频、频偏、低频调制信号和初始相位。表1为ZPW-2000A移频信号频率参数表[5]。

表1 ZPW-2000A移频信号频率参数表Table 1 Frequency table of ZPW-2000A FSK Hz

1.2 功率谱熵

(2)

功率谱熵的计算过程如下：先通过FFT变换得到信号的功率谱，再计算其信息熵得到功率谱熵。

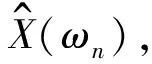
(3)

根据信息熵式(2)可以得到功率谱熵的公式(记作Hω，ω为频域)[7]：

(4)

功率谱熵可表征铁路移频信号的频谱结构。移频信号的能量在频率上分布越均匀，信号就越复杂，不确定度越大，谱熵也就越大[8]。

图1为某一类型轨道电路(载频1 700 Hz，低频10.3 Hz)正常状态时的功率谱图，计算其功率谱熵值为0.99.对其余频率配置时的轨道移频信号均求取其功率谱熵，可绘制出如图2所示的变化曲线。

图1 轨道移频信号的功率谱图Fig.1 Power spectrum of track FSK

图2 不同频率时的功率谱熵Fig.2 PSE curves at different frequencies

如图2所示，功率谱熵与低频调制频率有关，低频调制频率越大，谱线分布越集中，功率谱熵越小；而与载频几乎没有关系。对于轨道电路故障诊断，可以根据表征轨道电路状态的功率谱熵大小判断是否存在故障[8]。

图3为根据现场测回的移频信号数据所得的轨道电路处于不同故障状态时的功率谱图。由图可看出，轨端绝缘不良对移频信号功率谱图造成的波形畸变最为严重。

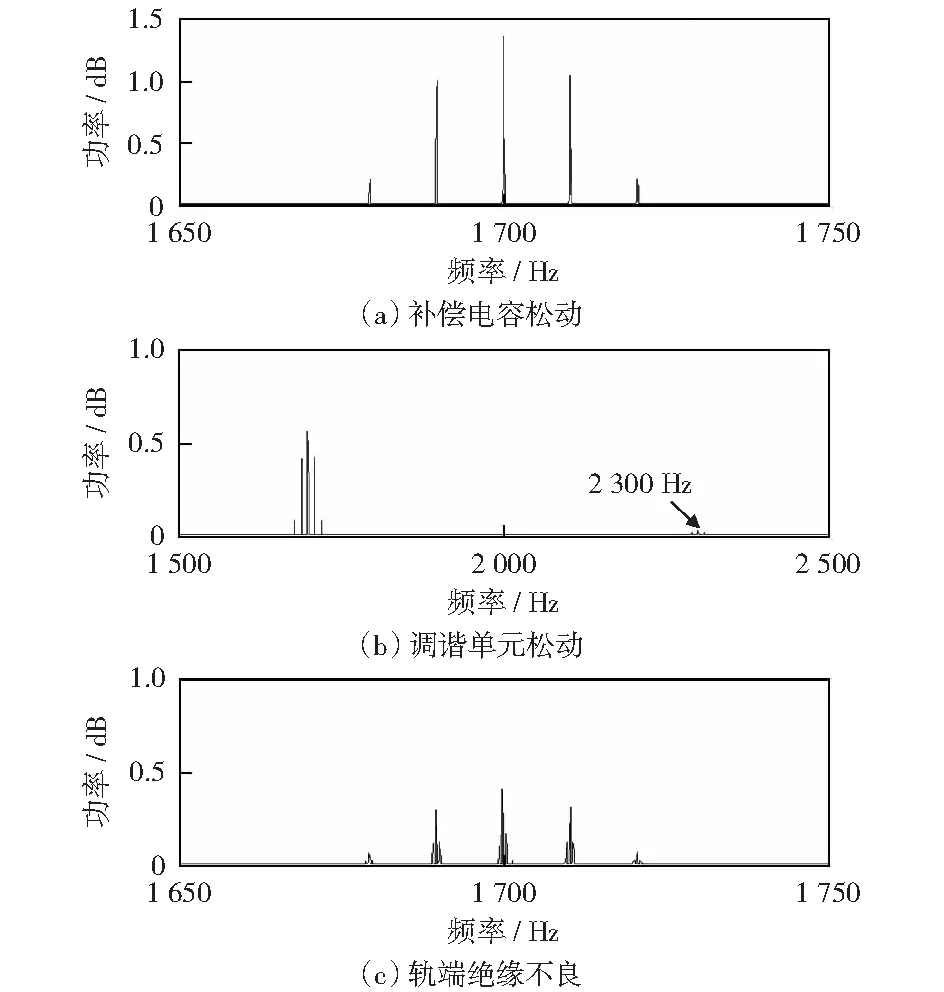
图3 轨道电路不同故障状态时的移频信号功率谱图Fig.3 Power spectrum of FSK under different fault states of track circuit

在轨道电路典型故障条件下，计算出的功率谱熵对于任何一种故障都有一定的分布范围。表2为根据铁路现场监测数据计算所得的轨道电路处于不同状态时的功率谱熵分布区间。

表2 轨道电路不同状态时的功率谱熵分布区间Table 2 Frequency table of ZPW-2000A FSK

然而，仅仅使用功率谱熵来诊断轨道电路的故障并不理想。如果未知故障类型的功率谱熵为1.26，则很难判断故障属于哪个状态[8]。因此，本文增加自适应神经模糊推理系统(ANFIS)，综合时域的幅值下降比、功率谱熵两种特征值，对轨道电路故障进行诊断。

2 ANFIS诊断模型

2.1 ANFIS概述

自适应神经模糊推理系统，简称ANFIS，它将神经网络的学习算法与模糊推理的简洁形式相结合，通过从训练数据集中学习产生数值解。因此，该模型不仅具有学习机制，而且具有模糊系统语言推理的优点[9]。

ANFIS结构有5层。假设模糊推理系统有两个输入，分别是x和y，输出是f，两者都是可用的数据对。网络中同一层中的每个节点均具有相似的功能；其中，O1,i表示第一层输出的第i个节点，其它依此类推。

第一层：模糊化层，对输入参数进行选择、模糊化。该层用节点函数表示的方形节点表示每个节点i，如下[10]：

O1,i=uAi(x),i=1,2 ;

(5)

O1,i=uBi-2(y),i=3,4 .

(6)

式中：Ai和Bi-2是语言变量，与节点功能相关，如“高”和“低”、“大”和“小”等等；或者说O1,i是模糊集A(A=A1,A2,B1,B2)的隶属度函数[11]，通常可以选用钟型函数：

(7)

式中：{ai,bi,ci}是隶属函数参数集。另外，梯形隶属函数(trapmf)、三角隶属函数(trimf)等均为常见的模糊化函数。该部分的参数集称为前件参数集[12]。

第二层：与运算层，计算模糊规则的激励强度。把两个输入信号的隶属度相乘，得到输出为：

O2,i=wi=uAi(x)uBi(y),i=1,2 .

(8)

第三层：归一化层。其公式为第i个节点的第i条规则wi与所有规则w之和计算得到的比值：

(9)

第四层：结论层。第i层的每个节点均为自适应节点，其输出为[10]：

(10)

第五层：去模糊化层。此层的单个节点是固定节点，将全部输入信号的总输出计算为[12]：

(11)

2.2 基于PSE-ANFIS的故障诊断模型

基于PSE-ANFIS的轨道电路故障诊断方法是采集轨道电路不同健康状态时的移频信号数据；提取故障数据特征，以此作为ANFIS故障分类器的训练样本、测试样本；最后，建立ANFIS 故障诊断模型，识别出轨道电路的故障模式，并输出最终的诊断结果[8]。其故障诊断模型如图4所示。

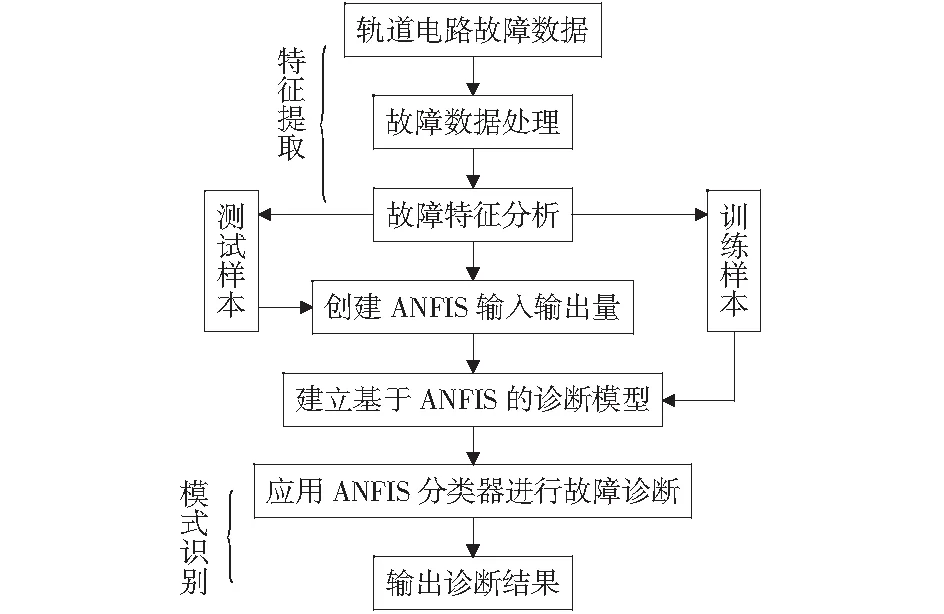
图4 基于PSE-ANFIS的诊断模型Fig.4 Diagnosis model based on PSE-ANFIS

3 轨道电路故障诊断系统

3.1 系统软件设计

以LabVIEW虚拟仪器为平台，通过Matlab与LabVIEW联合编程，采用模块化的设计方法，设计了在线监测、特征提取、故障诊断、安全预警、数据存储5个模块[5]。

3.1.1 特征提取模块

轨道电路故障时较正常状态时的移频信号幅值、功率谱熵均会出现一定的变化。因此本模块中主要对这两种特征量进行特征提取。

图5为特征提取模块的程序框图。

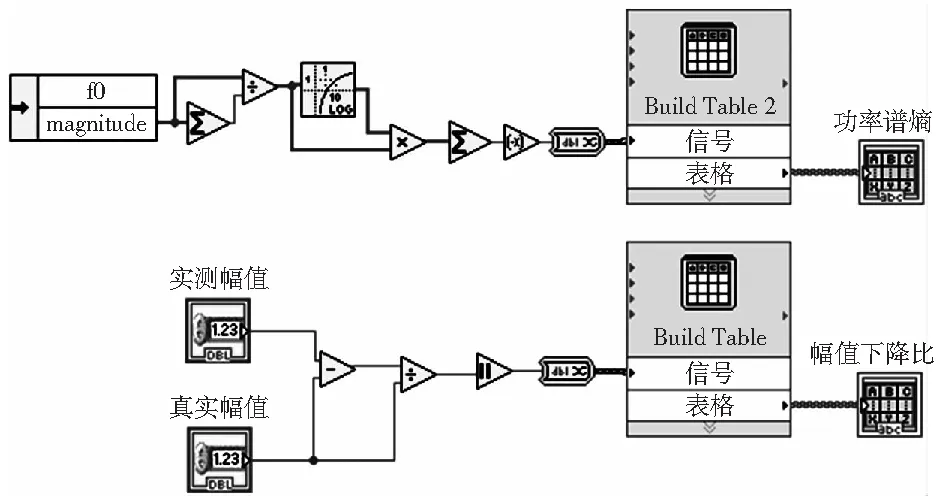
图5 特征提取模块程序框图Fig.5 Block diagram of feature extraction module

3.1.2 故障诊断模块

本文中的ANFIS模型为二输入单输出的结构。从铁路电务段收集轨道电路不同故障时的数据，每种故障状态100组数据，对数据进行处理，构成三维向量集[H1H2H3]，其中H1是“时域幅值较正常时的下降比”构成的向量，为输入向量；H2是“移频信号功率谱熵”构成的向量，也为输入向量；H3是“轨道电路状态编码”构成的向量，为输出向量：0表示正常状态，1表示补偿电容故障，2表示调谐单元故障，3表示轨道短路故障。再将向量集随机分成训练样本和校验样本，分别对ANFIS进行训练与测试，以建立ANFIS故障诊断模型[13]。

应用Matlab提供的anfis函数创建ANFIS网络，以gbellmf钟形函数作为初始隶属度函数，设置3条隶属度函数，进行30次训练。在LabVIEW中，ANFIS故障分类器的设计是采用Matlab script脚本实现的，将运行无误的Matlab程序导入到Matlab script脚本框中即可。