Group Lasso方法的脑功能超网络构建及分类研究
2018-11-15党伟超白尚旺潘理虎刘春霞
程 超,党伟超,白尚旺,潘理虎,2,刘春霞
(1.太原科技大学 计算机科学与技术学院,太原 030024;2.中国科学院 地理科学与技术学院,北京 100101)
静息态功能磁共振成像检测大脑自发低频神经活动,揭示相关神经活动的网络。基于功能性磁共振成像获得的大脑数据,已经提出相当多的脑功能连接建模方法,包括基于相关的方法[1]、基于偏相关的方法[2]和图形建模方法[3]。然而,基于相关的方法仅仅能够捕获成对的信息,因此不能全面反映多个脑区之间的交互。此外,基于相关的网络由于任意选取阈值有许多虚假的连接[4]。偏相关估计通常是通过使用逆协方差矩阵的最大似然估计(MLE)实现,而可靠的估计需要的数据样本规模要比建模的大脑区域数量大得多[5]。图形化的模型被用来研究大脑连接时缺少先验知识。
高阶信息对于疾病诊断可能是重要的,因为最近的神经科学研究认定在神经元同位素示踪、局部场电位和皮层活动中有重要的高阶交互[6]。为了将高阶信息应用于脑功能网络研究,提出了超网络构建方法[7]。超网络表示一种网络,它的每一条边代表多个脑区之间的交互作用。在已有文献中,脑功能超网络是使用稀疏线性回归方法构建;其中,求解稀疏线性回归采用的是LASSO(least absolute shrinkage and selection operator)方法。即使LASSO方法已成功应用于许多研究,它也存在局限:在超边构建时,选定一个脑区后,如果其它脑区之间存在较强的相关性,那么选择与选定有关的脑区时往往只随意选择存在组效应的一组脑区中的其中一个[8],可能还有一些相关的脑区无法选择出来,缺少解释分组效应信息的能力。本文考虑到脑区之间的组效应,提出将Group Lasso方法引入到超网络构建中,对超网络构建方法进行改善,然后根据构建的超网络提取3种关于大脑区域特定的特征(3种不同定义的聚类系数)。此外,利用非参数置换检验从3组聚类系数中选择最具差异的特征。最后,使用多核支持向量机在正常组和自闭症患者间进行分类模型构建。
1 材料和方法
基于超网络的脑网络分类方法包括几个主要步骤:数据预处理、超网络构建、特征提取和选择以及分类。
1.1 被试
本实验共收集53名被试,其中有25名自闭症患者,28名年龄性别匹配的健康志愿者作为对照组。自闭症患者数据来自公开的自闭症患者脑影像数据交换数据库(http://fcon_1000.proj ects.nitrc.org/indi/abide/).正常被试的数据采集工作是由山西医科大学第一医院进行的,所有的扫描工作由熟悉磁共振操作的放射科医生来完成。在扫描的过程中,要求被试闭眼、放松、不去想特定的事物但要保持清醒不能睡着。扫描参数设置如下:33 axial slices,repetition time (tR)=2 000 ms,echo time (tE)=30 ms,thickness/skip=4/0 mm,field of view (FOV)=192 mm×192 mm,matrix=64 mm×64 mm,flip angle=90°,248 volumes.
所有被试均被确诊为自闭症患者,通过自闭症诊断观察量表[9](autism diagnostic observation schedule,ADOS)及自闭症诊断访谈量表[10](autism diagnostic interview,ADI)来诊断。同时采用严格的排除标准:罹患严重的躯体疾病或神经系统疾病;妊娠或哺乳期妇女;体格检查发现有异常生化指标或脑电图、心电图异常者。所有被试的基本信息如表1所示。统计分析来评估组间差异,表中a表示双样本t检验,b表示皮尔逊卡方检验。

表1 被试基本情况统计Table 1 Demographics and clinical characteristics of the subjects
1.2 数据预处理
功能数据预处理是利用统计参数映射软件包(statistical parametric mapping software package,SPM8)进行。为了保证磁化均衡,每个被试前10个获得的功能磁共振图像被丢弃。剩余的图像进行时间片校正和头动校正,根据平移参数超过3 mm的标准,2例自闭组及2例对照组数据被排除。然后,图像进行12维度的优化仿射变换,将其标准化得到MNI(montreal neurological institute)空间标准回波平面成像EPI(echo-planar imaging)模板,重新采样成3 mm立方体素。由此产生的图像进行空间平滑并且消除线性趋势,最后进行低频滤波(0.01~0.10 Hz)以降低低频漂移及高频的生物噪音。
1.3 超图
图论是描述计算机科学中许多问题和结构的有力工具,已被广泛应用于脑网络分析[11]。大脑连接可以被简化为一个图的节点以及它们相互连接的边。节点和边的关系定义了网络的拓扑结构,可以通过描述网络结构的局部和全局属性来进行分析。然而,图只能描述一些二元关系,并不足以模拟一些复杂的问题或数据。事实上,除了两两之间的关系,在很多应用中,可能存在高阶的关系,不能用传统的图表示。为了克服这个局限,超图被提出用来描述节点之间的高阶关系。超图是图的扩展,它的超边是关于顶点的任意子集。这个概念模型比图论更符合一般的关系类型,并且已被应用于化学、工程和图像处理等许多领域。
一个超图H=(V,E),节点集合V,超边集合E,可以使用|V|×|E|维邻接矩阵表示H:
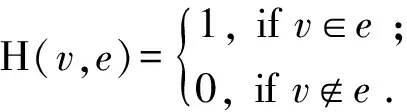
(1)
式中:v∈V是一个节点;e∉E是H的一条超边。
基于H,每个顶点v∈V的节点度是:

(2)
超边e的边度是:

(3)
1.4 超网络构建
每个被试的大脑空间通过自动解剖标记[12]模板进一步分割成90个感兴趣区域(region of interest,ROI).每个区域作为一个网络节点,同时该区域内所有体素的时间序列的平均值作为该节点的时间序列。每个脑区的平均时间序列进行了回归分析,以排除平均脑脊髓液和白质信号以及头动校正对信号的影响。以ROI作为网络中的节点,根据R-fMRI时间序列使用稀疏线性回归方法构建超网络,X=[x1,…,xm,…,xM]T∈RM×d表示一个训练被试,有M个ROIs,xm表示第m个感兴趣区域的平均时间序列,d是时间序列的长度。每个感兴趣区域的时间序列被视为一个响应向量,可以利用其他M-1个感兴趣区域的时间序列的线性组合估计:
xm=Amαm+τm.
(4)
式中:Am=[x1,…,xm-1,0,xm+1,…,xM]表示包含除了第m个ROI之外的其它ROIs的时间序列的数据矩阵;αm表示权重向量,衡量其它ROIs对第m个ROI的影响程度,非零元素表示相应ROIs与第m个ROI相互作用;τm表示噪声项。
1.4.1 传统基于Lasso方法的超网络构建
脑功能超网络是使用Lasso方法求解稀疏线性回归模型进行构建,这是l0范数问题,其优化目标函数为:
(5)
l0范数问题是一个NP问题,可以转化为l1范数问题求解。
(6)
式中:λ是控制模型稀疏的正则化参数。不同的λ值对应于不同的稀疏性的解决方案,较大的λ值表明更为稀疏的模型,即在αm中有较多的零。
在实验中,研究不同脑区之间的相互作用,对每一个被试构建超网络,以ROI作为节点,超边包括第m个ROI和其他在αm权重向量中非零元素对应的ROIs.为了反映大脑区域之间信息多层次的相互作用,对每一个ROI,通过在一个特定范围内变化λ值产生一组超边。在这里,多层次是指不同的λ值确定不同脑区之间的相互作用关系。也就是说,λ值较大的目标函数产生一个更为稀疏的解,因此超边包含更少的节点。具体地,在实验中,为了简单起见,改变λ值从0.1到0.9,增量为0.1.
1.4.2 基于Group Lasso方法的超网络构建
即使Lasso方法已成功应用于许多情况,它仍然存在一些局限。在超边构建时,选定一个脑区后,如果其它脑区之间存在较强的相关性,那么选择与选定有关的脑区时往往只随意选择存在组效应的一组脑区中的其中一个,而不关心是哪一个;还有一些相关的脑区无法选择出来,缺少解释分组效应信息的能力。
使用聚类方法将相关性强的脑区分为一组,再使用Group Lasso方法进行超边的构建可以帮助解决脑区之间的组效应问题。Lasso是用来选择单个变量[13],Group Lasso可以用来选择组变量,是在预先定义的变量组的基础上进行变量选择[14]。在进行超网络构建时首先要根据ROIs的平均时间序列进行聚类获得90个脑区的分组关系。在这里,采用了k中心点聚类法[15],首先计算脑区之间的两两相似度值,值越大表明两个样本越相似,并在此基础上进行聚类。对90个脑区进行聚类时,将其划分为k组,每个组表示一类对象,对象与组之间的关系必须满足:1) 每个组至少包含一个对象;2) 每个对象必须属于一个组。为了尽可能地保证聚类的稳定性,在选择k个初始化聚类中心时沿用k-means++[16]的思想,随机选择一个点作为第一个初始聚类中心,随后的每一个初始聚类中心是从剩余的数据点中以正比于数据点与存在的最近聚类中心点的距离的概率随机选择。重复聚类10次选取聚类效果最好的一组作为最终的聚类结果。在实验中,k的设置会影响到网络结构以及分类性能。经过研究发现,当k等于48时,会得到最高的分类准确率(详细分析在讨论中会提到)。然后使用Group Lasso选择脑区进行超边的构建,以下是优化目标函数:
(7)
式中:β是l2,1范数正则化参数,不同的β值对应不同的稀疏性,β值越大表明模型越稀疏,选择的组越少;αm通过聚类被分成了k个非重叠的组,αmGi表示第i个组。同样,为每个被试构建超网络,以ROI为节点,根据αm中非零元素对应的ROI构建超边。对每一个ROI,在一定范围内变化β值产生一组超边,改变β值从0.1到0.9,增量为0.1.
1.5 特征提取和选择
特征提取和特征选择是机器学习中的关键预处理步骤。在实践中,不能知道当前的特征是否与问题有关,不相关的特征增加了预测模型的复杂性,降维方法的应用有助于模型的建立和模型预测性能的改善。在这里,特征提取主要包含3个指标的计算,即三个不同定义的聚类系数[17],这3种聚类系数从不同角度衡量了超网络的局部属性。
给定一个超网络H=(V,E),u,t,v表示节点,e表示超边,vS={ei∈E∶v∈ei}表示包含节点v的一系列超边,vN表示包含节点v的超边含有的其它节点的集合。然后,3种不同类型的聚类系数在节点v上可以被定义,分别如下:
(8)
(9)
(10)
如果∃ei∈E,例如u,t∈ei,但是v∉ei,则I(u,t,v1)=1,否则等于0.如果∃ei∈E,例如u,t,v∈ei,则I'(u,t,v)=1,否则等于0.
对于每一种聚类系数定义,分别从超网络中提取作为特征,从而每个被试产生三组特征。特征选择的目的是从原始特征集合选择最具代表性的最优特征子集。为了选择与自闭症病理有关的关键的特征,采用统计分析方法非参数置换检验来评估自闭症患者和正常对照之间的差异性,将具有显著组间差异(p<0.05)的局部属性作为分类特征进行分类模型构建。
1.6 分类
选择RBF(radial basis function)核函数以及LOO(leave-one-out)交叉验证来进行分类以及评估所提出方法的性能。具体而言,一个被试用于测试,其余的用于训练以建立模型。对于每个被试,整个过程重复进行并且选取分类准确率的算术平均值作为最终的分类结果。多核分类方法的参数是基于训练被试的网格搜索(范围从-8到8,步长为1),通过k折交叉验证方法得出训练集验证准确率并进行比较确定。此外,对于每一种类型的聚类系数,共有90个特征从所构建的超网络中提取。对于每个提取的特征,从训练被试中计算平均值和标准偏差进行标准化。
2 实验和结果
2.1 差异性的脑区
基于Group Lasso方法,对脑区的特征进行非参数置换检验所有被试评估自闭症患者和正常志愿者之间的差异。统计分析结果表明,与对照组相比,在自闭组中出现显著异常的脑区主要在部分边缘系统区域(双侧内侧旁扣带脑回,右侧海马,右侧海马旁回,右侧后扣带回),部分额叶区域(左侧三角部额下回,左侧眶部额下回,双侧中央旁小叶),以及部分顶叶区域(右侧角回,左侧楔前叶)等(表3)。选定的特征p值小于0.05(已校验),表明患者和正常人之间的差异较大。表2列出了这些异常的脑区。图1展示了在模板空间的这些大脑区域。

表2 基于Group Lasso方法得到的异常脑区及其显著性Table 2 Different bode attributes based on group lasso
2.2 分类准确率
本文提出的基于Group Lasso的超网络的脑网络分类方法与原有的基于Lasso的超网络的脑网络分类方法以及传统的连接网络分类方法进行了比较。传统连接网络方法采用皮尔逊相关,在稀疏度为5%~40%下构建所有被试的功能脑网络,进行度、中间中心度、节点效率3个局部指标的计算,为表征指标在所选阈值空间内的整体特性,计算每个指标的AUC(area under curve)值,选择非参数置换检验后具有显著组间差异的局部属性的AUC值作为分类特征。同时,也与其它利用脑网络特征对自闭症进行分类的研究进行了比较。分类结果如表3所示。

图1 基于Group Lasso方法得到的异常脑区Fig.1 Discriminative brain regions based on Group Lasso

表3 关于自闭症分类方法的分类性能比较Table 3 Comparison of classification potential evaluation of classification methods
3 讨论
在基于超网络的脑网络分类中,网络构建是非常关键的。在现有研究中已经提出了许多功能网络模型,但大多数是基于简单图,只反映成对的大脑区域之间的相互作用关系。本文基于超图理论构建超网络模型,用于描述多个脑区之间的高阶相互作用。这种高阶相互关系可能包含有用的信息用于识别患者和正常人,并且在此基础上提出了新的超网络构建方法。研究结果表明,基于超网络的脑网络分类方法可以提高分类性能,并且与原有超网络构建方法相比,基于Group Lasso的超网络构建方法可以实现更好的分类结果。同时,与其它文献中的分类结果相比也可以得到一定的改善。
基于Group Lasso的超网络构建方法,经过统计分析可以得到一些具有组间差异的脑区。这些区域主要集中在边缘系统、额叶以及顶叶,其中,海马、后扣带回、角回等区域均为默认网络关键区域。在自闭症的病理研究中,默认网络被广泛认为是自闭症的主要病理环路[22]。
本文提出的方法会受到一些参数的影响,其中,参数k是Group Lasso方法中进行聚类的组数,选取不同的k会得到不同的网络结构以及分类结果。为了比较k对于分类性能的影响,设置k的变化范围为[6,90],步长大小为6.由于第一个初始种子点的随机选择会造成结果的差异,分别在每一个k值下进行50次实验,选取正确率的算术平均值作为最后的分类结果。图2展示了实验结果,结果显示当k=48时,最高正确率达到87.84%.

图2 不同k值对应的分类准确率Fig.2 Classification accuracy of different k values
如图2所示,当k值较小或较大时,即网络构建约束过于紧张或过于宽松时,分类正确率都比较低。这一结果表明,适中的连接构建约束可以得到更为有效的分类结果,而过于严格或宽松的构建策略,均无法达到满意的效果。
4 结束语
本文将稀疏线性回归模型用于构建超网络,计算相关指标并选择具有显著组间差异的指标作为分类特征,利用脑区之间的高阶关系来进行自闭症患者与正常人的分类。实验证明,基于超图的脑网络分类方法不仅可以改善大脑的疾病分类,也便于与疾病有关的结构的检测。此外,基于Group Lasso的超网络构建方法可以较好地解决分组效应,选取相关程度比较大的脑区,改善分类性能。
在目前的研究中,基于Group Lasso的方法由于第一个聚类初始种子点的随机选取以及聚类数k的不同会造成网络结构以及分类结果的不唯一。接下来,如何建立更加稳定的超边则是后续工作的重点。
