基于遥测电流的太阳翼在轨振动参数辨识方法

吴跃民，刘志全，任守志

(中国空间技术研究院总体部，北京 100094)

0 引 言

随着航天技术的发展，大尺寸太阳翼已成为当今航天器的主流配置[1]，但由于结构挠性的存在，太阳翼在轨振动会降低航天器本体姿态和轨道控制精度，引起航天器性能下降甚至失效[2-5]，而进行振动抑制的前提是准确辨识其固有频率、阻尼比等振动特性参数(下文简称振动参数)。太阳翼地面展开试验过程难以完全消除重力、空气阻尼等影响，地面条件下开展的太阳翼振动参数测试与对应的在轨测试相比误差较大[6-7]，而计算分析手段同样难以获得较为真实、可信的结果[8-9]，因此，太阳翼振动参数在轨辨识方法的研究已成为国内外学者的研究热点之一。

常见的振动参数在轨辨识方法主要有航天器姿态角速度波动辨识法、影像测量辨识法和振动传感器测量辨识法。

1994年1月，NASA用姿态角速度波动辨识法对哈勃望远镜实施了专门的在轨振动测试[10]，利用姿态角速度波动辨识法识别到太阳翼部分振型与固有频率信息，但其所用高精度速率陀螺、快速控制系统并非为一般航天器所能配备。

1995年11月，美国JPL(Jet Propulsion Laborato-ry)基于影像测量辨识法策划并实施了首个太阳翼在轨振动特性测量试验[11]。用架设在航天飞机上的摄像机拍摄“和平号”空间站太阳翼在某些激励事件下的振动影像，对其进行数字化处理后再利用图像识别方法获得特征点的振动信息，最终识别出太阳翼在轨振动固有频率、振型、阻尼比等。虽然该试验取得了成功，但整个测试系统过于复杂。

若将摄像机安装在被测航天器上进行测试，将难以识别到振动量级较小的翼面振动信息，也难以适应振动量级较大、测试基准发生变化的情况。2013年哈尔滨工业大学许畅等提出的基于双目视觉的大型挠性结构模态参数辨识方法[12]以及2016年北京航空航天大学吴小猷等提出的基于视觉测量的太阳翼模态参数在轨辨识方法[13]均未明确摄像机的架设位置，均存在类似的问题。

2004～2013年，清华大学周舟[14]、哈尔滨工业大学李逍然[15]、北京航空航天大学赵寿根[16]、中国空间技术研究院于登云[17]等相继开展了振动传感器测量辨识方法研究，但振动传感器、信号采集等设备安装代价较大，且影响太阳翼在轨振动特性。目前尚未见到基于振动传感器测量辨识法的在轨实际应用的文献。

针对上述辨识方法存在的问题，本文提出一种无需额外增设测量设备，仅依靠遥测电流波动信息来辨识太阳翼在轨展开状态振动参数(固有频率、阻尼比)的方法，并结合某太阳翼实际飞行数据进行应用验证。

1 在轨振动参数的辨识方法

1.1 辨识原理

当航天器变轨或进行姿态机动时，太阳翼上将会产生一定量级的振动，各太阳电池片的受照状态将随之发生变化，进而引起整个太阳翼或某个区域发电电流产生波动。以图1所示太阳翼及光照条件为例，假定该太阳翼整翼或某个区域内共有m个状态完全相同的太阳电池片，在某一时刻第i(i=1，2，…，m)个电池片法线与太阳入射光线之间的夹角(入射角)为θi，则m个电池片在该时刻的发电总电流I可以表示为

(1)

其中，Imax表示单个太阳电池片在太阳光垂直照射时可获得的最大发电电流；f(θi)表示与入射角θi相关的折减系数。依据文献[18]的测试结果，当θi在0°～60°时，f(θi)≈1；当θi增大到70°时，f(θi)≈0.89；当θi增加到85°时，f(θi)≈0.42。

图1 太阳翼在轨工作时的光照条件Fig.1 In orbit solar wing light conditions

太阳翼在轨平稳运行时，θi保持不变，I的时间历程函数I(t)趋于稳定。当太阳翼在轨振动时，θi随之发生变化，I(t)将出现与之相对应的波动。如果太阳翼在轨振动是由单个或多个阶次振动的叠加，则I(t)中的波动部分也将能对其进行如实反映，进而可以利用该波动对太阳翼在轨振动参数进行辨识。

1.2 辨识方法及流程

为便于说明，以图1所示太阳翼为例，将其展开状态模态分析结果导入Adams软件，在远离星体的最外侧角点处施加阶跃型激励，使其产生多个阶次的自由振动，可得如图2所示的发电电流模拟信号。对该信号进行傅里叶变换，所得幅频响应曲线如图3所示。

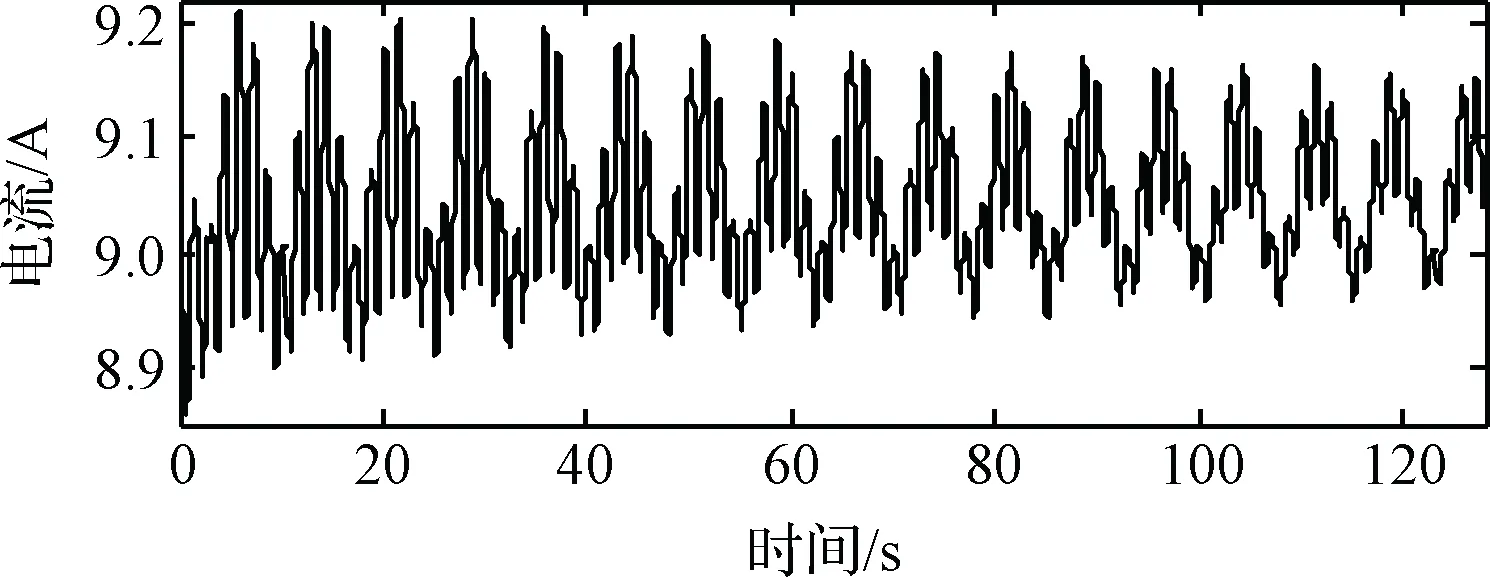
图2 发电电流模拟信号Fig.2 Simulated current signal

图3 幅频响应曲线Fig.3 Amplitude-frequency response curve

从图3可见，在0.1405 Hz、0.7108 Hz和0.8436 Hz 附近幅频响应曲线上有明显峰值，说明原始电流信号中包含有这3个频率的振动信息。进一步对比分析可知，这3个频点分别与该太阳翼第1阶、第3阶、第4阶固有频率相对应。可见，结合模态分析结果与太阳翼在轨振动期间获取的I(t)中的波动信号傅里叶变换结果即可实现对太阳翼在轨振动固有频率ωj(j=1，2，…)以及阶次j的辨识。

获取ωj后，利用滤波算法对I(t)中的波动信号进行滤波，得到仅与ωj相关的分量信号Ij(t)，该信号的衰减特性即可表征太阳翼第j阶在轨振动的衰减特性。如果I(t)中仅包含单个阶次的振动信息，则I(t)的衰减特性即可表征太阳翼对应阶次在轨振动的衰减特性。

假定第j阶振动信号如图4所示，其对数减幅率dj(波峰衰减系数的自然对数)可表示为

(2)

其中，Pk和Pk+1分别表示第k个和第k+1个波峰值，k=1，2，3，…，n。

图4 第j阶振动信号Fig.4 Vibration signal of order j

阻尼比ξj可表示为

(3)

利用航天器自带的太阳翼发电电流采集系统与遥测通道获取与I(t)中的波动信号相对应的遥测电流信号R(t)后，则可以按以下流程进行太阳翼在轨振动固有频率ω以及对应阻尼比ξ的辨识：

1)对R(t)进行傅里叶变换，得到与之对应的幅频响应曲线；

2)结合模态分析所得固有频率大小以及振型信息，判断幅频响应曲线上局部峰值对应固有频率ωj以及阶次j；

3)以ωj为中心，设计合理的滤波器对R(t)进行滤波处理，得到仅包含第j阶振动的衰减振动信号Rj(t)；

4)利用Rj(t)振幅衰减特性计算与ωj对应的阻尼比ξj。

2 辨识方法的应用范围及辨识误差分析

2.1 辨识的前提条件

利用遥测电流信号进行太阳翼在轨振动固有频率辨识有3个基本条件：

1)对应阶次的振动被激起；

2)该阶振动能够引起发电电流的波动；

3)电流波动能被准确获取。

第1)项与航天器在轨所受扰动相关，第3)项取决于航天器自带的太阳翼发电电流采集与传输系统性能，而第2)项则与太阳翼振型及初始的光照条件相关。

为获得太阳翼振型与I(t)中的波动信号之间的关系，以图1所示太阳翼为例，利用有限元方法获取其在轨飞行状态的前4阶振型如图5所示。其中，第1阶为垂直于翼面方向的振动，第2阶为平行于翼面的振动，第3阶为绕整翼长轴方向的扭振，第4阶为垂直于翼面方向的高阶振动。

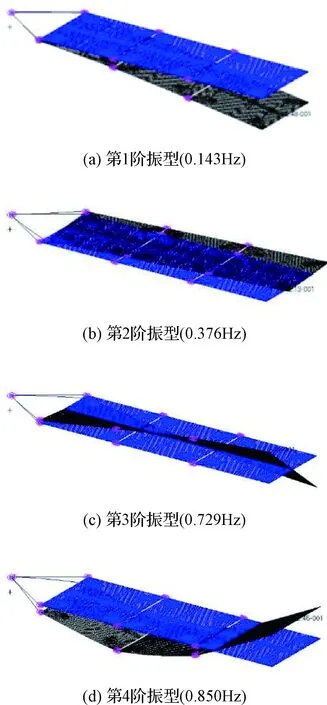
图5 太阳翼模态分析结果Fig.5 Modal analysis results of deployed solar wing

在图1所示光照条件下，当整个太阳翼产生第1阶、第3阶、第4阶振动时，各电池板内每一个太阳电池片所对应的实际光线入射角θi均会发生变化，进而会引起I(t)产生波动。但是，对于第2阶振型来说，无论其振幅如何,各太阳电池片对应的光线入射角θi始终不变。即使该阶振动被激起，I(t)信号中也不会出现波动信息。

在图5所示的第1阶、第3阶振型下，太阳翼所有电池片对应的实际光线入射角θi变化趋势是一致的，但对于图5所示第4阶振型来说，各电池片对应θi的变化趋势不尽相同，局部区域(如内板)电池片发电电流的累加结果与整翼累加结果相比，波动量将更为显著。

除了电池片所在区域与太阳翼振型因素外，初始光照条件也会对I(t)波动量的大小产生影响。假定振动过程中太阳翼翼面经过平衡位置时各电池片对应光线入射角为θi0，振动过程中相对于θi0的最大变化量为αi，则由式(1)可知：

(4)

其中，δ表示I(t)在太阳翼振动过程中的最大波动量。

为便于分析，假定θi0=θ0、αi=α，则式(4)可简化为：

(5)

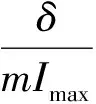
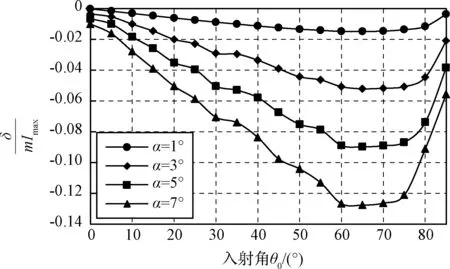
图与α、 θ0的关系Fig.6 The relationships of and α, θ0

由图6可见：

1)当θ0一定时，δ随着α取值的增大而增大，说明太阳翼在轨振动量级越大，I(t)中的波动量越大。

2)当θ0=0°～45°之间时，无论α取值如何，δ均处于较低水平。说明太阳光线接近垂直照射太阳翼时，即使整翼振动幅值较大，I(t)的波动水平也比较有限。这也就是在展开后立即转入对日定向模式(θi=0°)的常规太阳翼难以观测到遥测电流波动的根本原因。

3)当θ0在80°以上时，无论α取值如何，δ也将处于较低水平。其主要原因是太阳光线接近平行照射太阳翼时，折减系数急剧减小，导致I(t)以及其波动量急剧降低。

上述结论虽然是在太阳翼所有电池片均同步振动的条件下获得的，但利用有限元工具进行的仿真计算结果也可以证明：相同振动量级下，与其它取值区间相比，初始入射角θ0在45°～80°之间时，I(t)中的波动量较大。

2.2 辨识误差分析

本文所述辨识方法采用的基础数据是航天器太阳翼在轨发电电流遥测量，是典型的离散信号，如果其采样频率过低，则无法再现I(t)中的波动信息，也就无法表达太阳翼在轨的振动情况。根据香农采样定理的要求，在进行太阳翼固有频率辨识时，R(t)信号的采样频率至少应达到对应固有频率的2倍以上。

另一方面，在辨识固有频率时，用到了离散傅里叶变换，其频率分辨率Δω为

(6)

其中，fs表示采样频率，N为采样点数。

由式(6)知，在fs不变的前提下，N越大Δω数值越小。而N的上限取决于I(t)中的波动量能够被航天器自带的电流采集系统准确识别的信号总长度，简称有效信号长度。假如某I(t)的有效信号长度为128 s，对相应的R(t)信号进行傅里叶变换时，Δω不会超过0.0 078 125 Hz。如果被辨识的振动频率为0.2 Hz，则由于傅里叶算法本身带来的最大误差为3.9%。

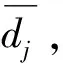
(7)

为尽可能降低波峰值采样误差对计算结果带来的影响，可采用最小二乘法对所采集到的n个波峰值衰减规律进行指数函数拟合(如图7所示)，然后利用拟合曲线任意提取Pk与Pk+1，再利用式(2)计算dj，用式(3)计算ξj。

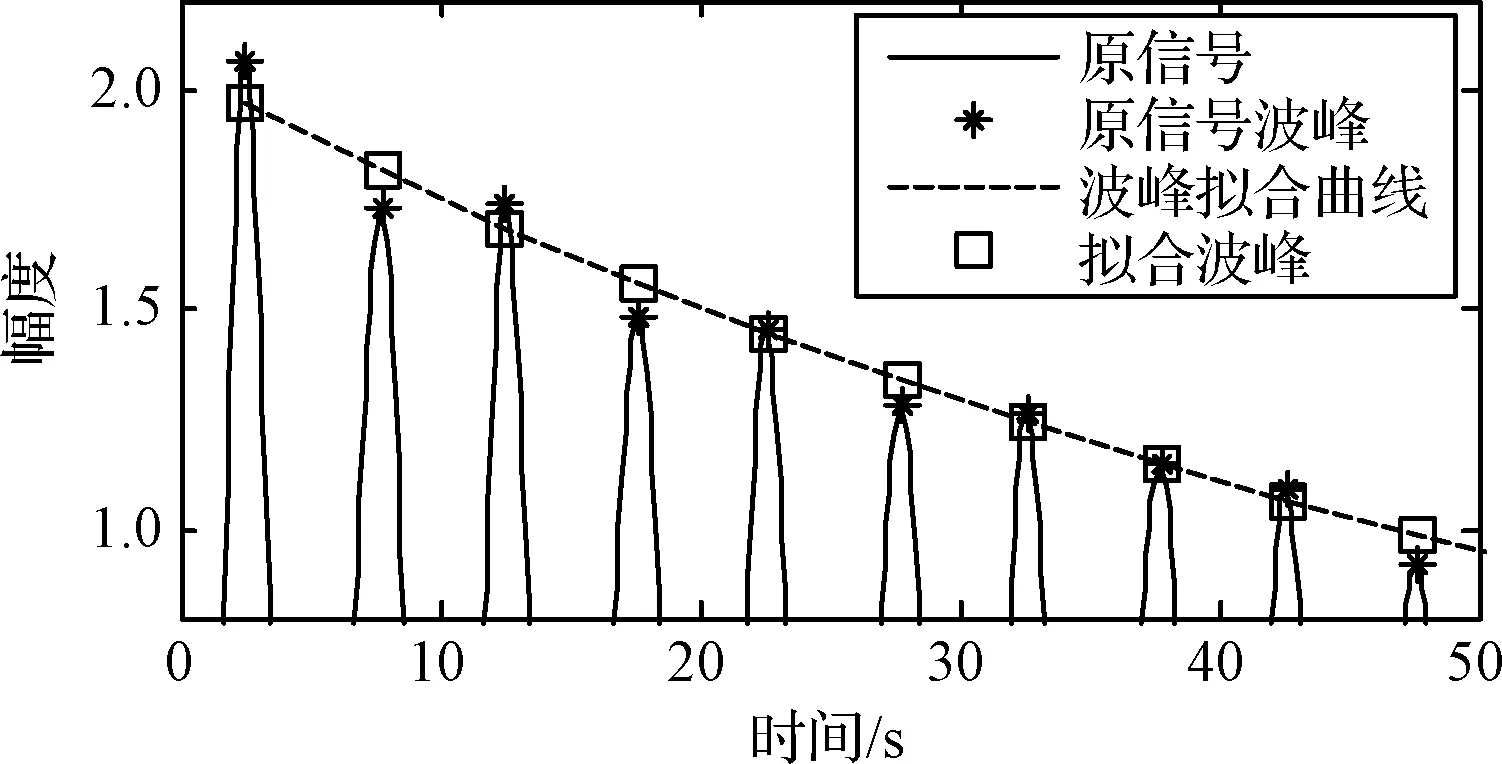
图7 波峰值衰减规律拟合曲线Fig.7 Peak attenuation fitting curve

除了上述数据处理方法外，在进行阻尼比计算时，R(t)信号的采样频率、采样精度以及在后续处理中用到的滤波器性能等均有可能对计算结果产生影响。考虑到滤波器的设计及参数选择与R(t)信号的具体形态关系密切，难以统一确定，因此，此处仅针对采样频率、采样精度两个因素进行误差水平分析。

取阻尼比ξ=0.01，固有频率ω=0.15，构造式(8)所示单自由度衰减振动信号y(t)。分别取y(t)最大幅值的0%、0.25%、0.50%、1.00%为采样误差，并分别以0.5Hz、1Hz、2Hz、5Hz频率进行采样，构造R(t)信号，利用100次计算得到的最大阻尼比计算误差见表1。

(8)

表1 不同采样频率及采样误差下最大阻尼比计算误差Table 1 Maximum damping ratio calculation error at different sampling frequencies and sampling errors

从表1可以看出，1 Hz采样频率、最大幅值1%的采样误差下，利用本文所述方法计算阻尼比时误差不超过3.01%，可满足工程应用需求。

3 仿真校验

为进行辨识算法验证与误差量级评估，构造式(9)所示由3个单自由度信号叠加而成的复合信号x(t)作为研究对象进行分析。其中，Aλ、ωλ、ξλ、φλ分别表示第λ个分量信号的幅值、固有频率、阻尼比与初始相位角，ψ表示与采样误差相对应的随机系数，ψ∈[0,1]。

(9)

表2 算法验证参数及结果Table 2 Algorithm verification parameters and results

任取A1=3，A2=3.5，A3=4，φ1=10，φ2=5，φ3=5，ωλ与ξλ取表2所示理论值，并以10 Hz频率进行采样，最终合成信号及3个单自由度信号分量见图8。

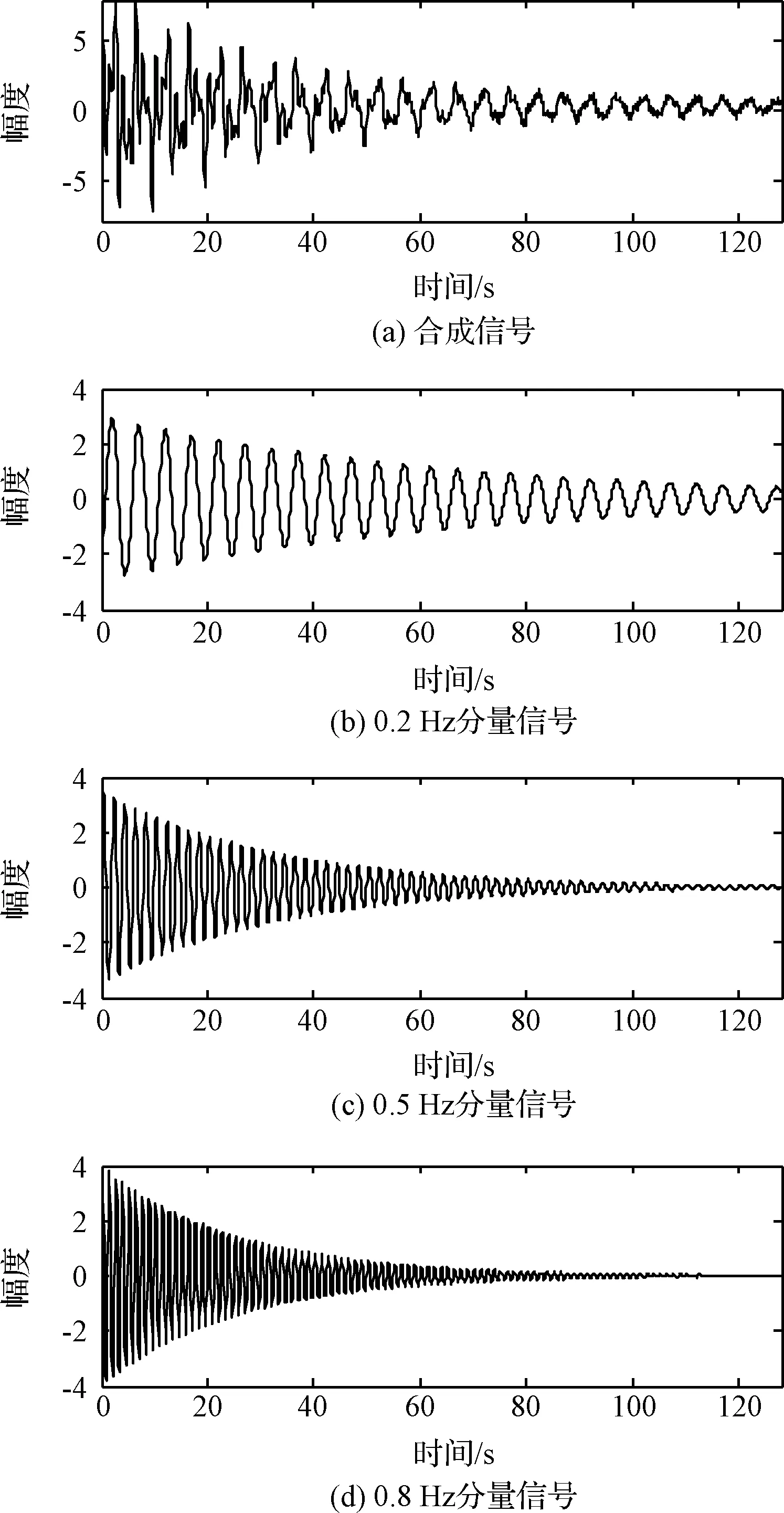
图8 合成信号及其分量信号Fig.8 Composite signals and their component signals

对图8所示合成信号进行傅里叶变换，结果如图9所示。

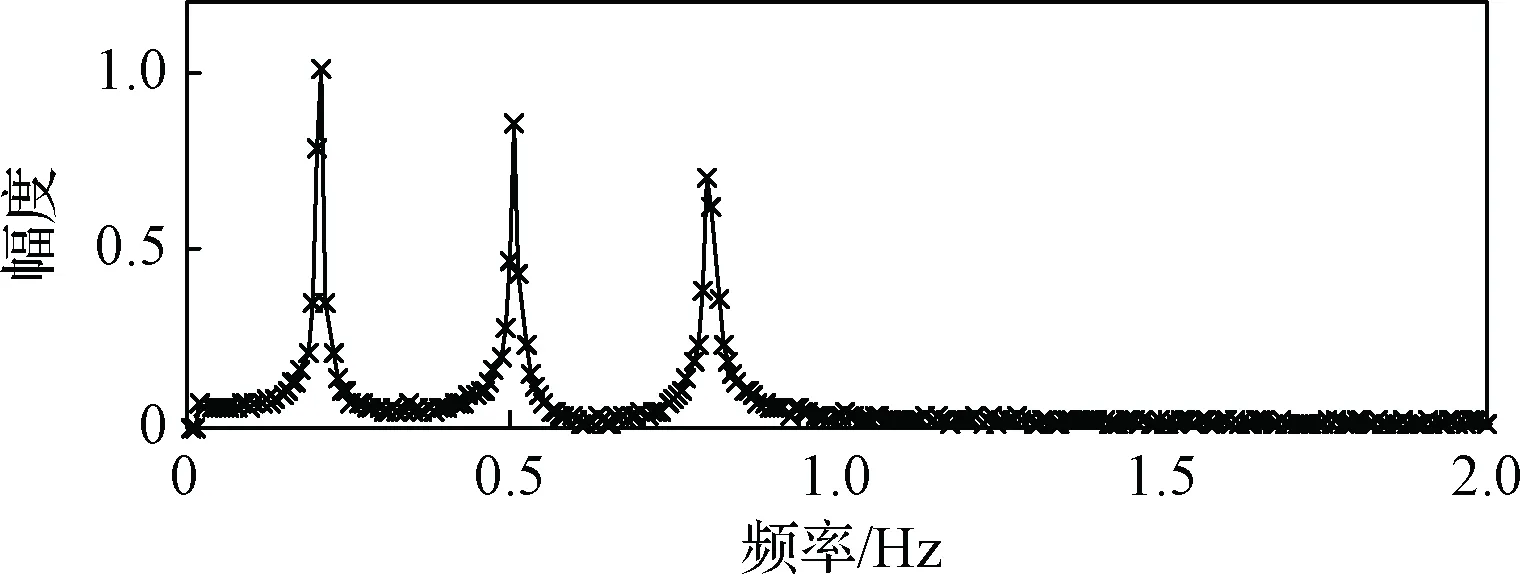
图9 合成信号对应幅频响应曲线Fig.9 Amplitude-frequency response curve of composite signal

图9中较为明显的3个峰值频点即与合成信号的3个固有频率相对应，其数值分别与理论值0.2 Hz、0.5 Hz、0.8 Hz固有频率相对应，最大偏差为5.5%(详见表2)。分别以这3个频点为中心，设计巴特沃斯带通滤波器，滤去其它两个峰值频点附近的信号，可得到3组分量信号，如图10所示。

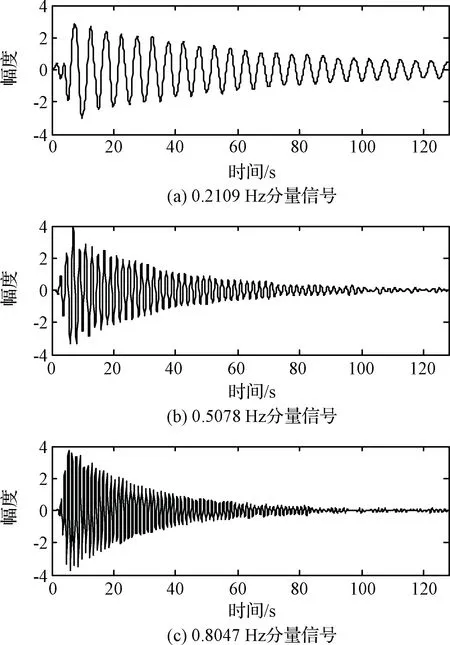
图10 带通滤波所得分量信号Fig.10 Band-pass filtered component signals

对比图8与图10可知，滤波后所得信号前端与原分量信号之间存在一定的差异，但其后端的衰减特性与原分量信号基本一致。按照本文2.2节所述基于最小二乘法的计算方法对图10所示信号进行阻尼比计算，结果如表2所示，最大偏差为3.0%。

可见，即使存在一定的随机误差(或采样误差)，本文所述方法仍具有较高的辨识精度，完全满足工程应用要求。

4 在轨应用示例

通过遥测手段获取的某卫星太阳翼在轨振动期间R(t)信号如图11所示。从中可见，太阳翼发电电流存在明显波动，且随着时间的推移振幅逐渐衰减，最终趋于稳定。

图11 某太阳翼R(t)信号Fig.11 R(t) signal of a certain solar wing

对图11所示电流随时间变化曲线进行傅里叶变换，结果见图12。

图12 遥测电流信号对应幅频响应曲线Fig.12 Amplitude-frequency response curve of telemetry current signal

如不计低于0.02 Hz的低频分量(主要由卫星本体振动引入)，则图12中有且只有1个峰值频点，可辨识为太阳翼在轨振动的1阶固有频率(0.1484 Hz)。该频率与图5所示1阶垂直于翼面方向的振动固有频率分析值(0.143 Hz)基本吻合。

设计滤波器对图11所示信号进行处理，消除0.1484 Hz附近频段以外的其它分量信号，结果如图13所示。按照本文2.2节所述基于最小二乘法的计算方法进行计算，阻尼比为0.0168。

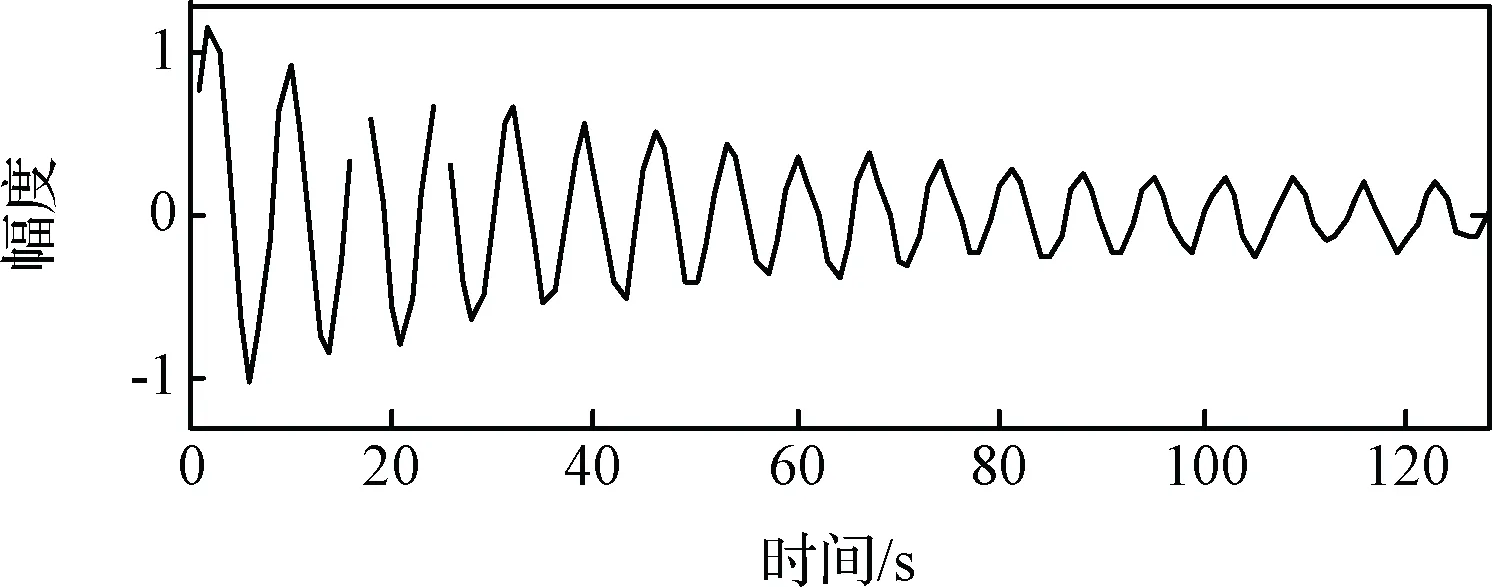
图13 0.1484 Hz分量信号Fig.13 0.148 Hz component signal

5 结 论

遥测电流波动信息可反映太阳翼在轨振动的某些固有特性。本文据此提出的太阳翼在轨振动参数辨识方法无需增设额外测量设备，仅依靠航天器自带的太阳翼发电电流采集系统与遥测通道获取的信息即可对太阳翼在轨振动参数进行辨识，该方法简单、直观，且得到了工程验证。