上面级发射中高轨道卫星外热流分析

杜卓林，江 海，陈少华，金 迪

(1.北京空间飞行器总体设计部，北京 100094；2.空间热控技术北京市重点实验室，北京 100094)

0 引 言

上面级是在基础级火箭上面增加的相对独立的一级或多级，可将一个或多个航天器直接送入预定工作轨道或预定空间位置[1-4]。与传统运载火箭几十分钟的飞行时间不同，采用上面级发射的中、高轨道卫星飞行时间可达3.3～6.5小时[2]，需要较长时间经受太阳辐照、地球红外辐射、地球反照、真空、冷黑等空间热环境。在这一阶段，卫星姿态、设备工作模式、太阳翼的收拢状态以及整星热控加热功率的约束等都同工作轨道有较大差别，热控设计需要在满足工作轨道在轨任务的前提下，同时兼顾上面级发射轨道的热控需求。而对上面级发射轨道卫星极端热流工况和外热流的准确分析是进行热控设计的前提。

上面级发射轨道可近似视为一非封闭倾斜椭圆轨道。根据理论分析[5]，对于倾斜轨道，β角(阳光与轨道面之间的夹角)会随着太阳黄经和升交点赤经变化很大，造成卫星各个面的受照情况复杂。此外，在轨道高度较低时，外热流分析不仅需要考虑太阳辐射，还需要考虑卫星与上面级组合体慢旋姿态下的地球红外辐射和地球反照。再次，上面级非封闭大椭圆轨道的特点，使其外热流和地影时间的计算要比封闭圆形轨道复杂很多。以上这些因素使采用上面级发射的卫星外热流变化非常复杂，极端外热流工况难以判断。

国内对卫星工作轨道的外热流研究已开展了大量的工作。文献[6-8]对圆形太阳同步轨道卫星的外热流进行了深入研究。文献[9]推导了国际空间站圆形轨道太阳辐射热流计算公式，分析了太阳辐射热流随轨道参数的变化。文献[10]对倾斜轨道临界β角的变化规律进行了分析，并利用软件计算了卫星太阳翼吸收的外热流。文献[11]通过对轨道空间外热流的理论分析，推导出了倾斜轨道六面体卫星空间外热流的理论模型。文献[12]对封闭的大椭圆轨道太阳照射问题进行研究，给出了某三轴稳定卫星大椭圆太阳同步轨道的外热流分析结果。相比而言，对于上面级发射轨道卫星外热流的研究目前开展较少。文献[13]对某运载火箭上面级热环境进行了分析，确定了热分析和热试验的两个极端工况：最大外热流和无任何热流工况，显然该外热流条件选取过于苛刻，与实际的极端热流工况偏差较大。文献[14]给出了上面级轨道太阳矢量和受晒因子随发射窗口的变化关系，以及上面级各端面极端外热流工况所对应的太阳矢量和上面级纵轴的夹角，但文中未对滑行段慢旋、点火段姿态等影响因素进行具体分析。

从上述文献可知，目前对采用上面级发射的卫星轨道外热流研究还有待深入开展。鉴于此，本文给出了上面级发射轨道卫星外热流计算方法。以北斗三号中轨导航卫星为例分析了阳光和轨道面夹角、阴影时间、滑行段旋转角速度等因素对外热流的影响，确定了卫星的极端外热流工况并给出了外热流分析结果。分析结果为进一步开展整星和星外部件的热分析及热试验工作提供了重要依据，同时也对如何选择发射窗口以规避极端工况、改善卫星飞行热环境具有一定的指导意义。考虑到上面级发射轨道的相似性，本文的研究工作对采用上面级发射的中高轨通信导航卫星、深空探测卫星的外热流分析具有参考意义。

1 上面级轨道外热流分析方法

采用上面级发射的中、高轨道卫星通常采用承力筒结构或桁架式结构，整星分为服务舱、载荷舱和推进舱，其中载荷舱、服务舱分别由相对独立的±Y、±X等舱板组成。根据卫星工作轨道的外热流情况，卫星散热面选取在卫星的±Y面，以及采用偏航控卫星的+X(或-X)面。由于各舱板相对独立，互相之间的辐射和导热影响较小，因此后续分析中主要针对单板展开。

1.1 上面级轨道及卫星姿态描述

上面级轨道由两个阶段组成，如图1所示。卫星与上面级组合体在近地点与运载基础级分离后，沿着椭圆轨道飞行，该阶段为上面级滑行段。卫星与上面级组合体飞行至远地点附近时，通过上面级发动机点火将卫星送至工作轨道，该阶段为上面级点火段。上面级轨道点火段理论上是由无限个亚轨道或轨道弧段组合而成，为了便于分析，本文将上面级点火段简化成椭圆轨道的一部分，整个上面级轨道可以视为一个非封闭的椭圆轨道。上面级阶段相关轨道参数见图1，其中β为阳光和轨道面的夹角，Ω为升交点赤经，Λ为会日点(从近地点算起)，ω为椭圆轨道近地点幅角(从升交点算起)。

上面级滑行段飞行时，通过上面级姿态控制，阳光矢量和上面级纵轴(卫星的+Z轴)保持一个固定的角度，为避免滑行段卫星和上面级某一侧散热面出现长期受照的情况，通常上面级会采用绕其纵轴慢速旋转的控制策略。上面级点火段可近似看成一个三轴稳定的姿态，卫星-Y轴指向地心，卫星+X轴指向轨道面法线方向。

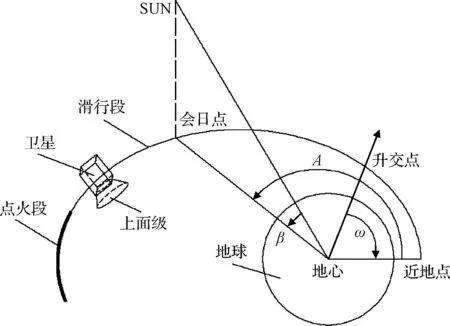
图1 上面级轨道示意图及相关轨道参数Fig.1 Launch orbit for upper stage and related parameters

1.2 上面级轨道外热流计算方法

1.2.1滑行段

1)太阳辐射热流

滑行段卫星绕其Z轴旋转，阳光和+Z轴的夹角保持不变，卫星+X、+Y、-X、-Y面轮流受照，时间依次相差1/4旋转周期，因此选取四个面中的一个进行研究即可，本文选取卫星的+X面。太阳辐射热流可表示为：

q1-Z=ScosψS

(1)

q1-+X=SsinψSsinφS

(2)

式中:S为太阳常数。ψS和φS定义见图2。

图2 滑行段星体坐标系下太阳矢量示意图Fig.2 Vector to the Sun in body coordinate system during coast phase

2)地球红外辐射热流和地球反照热流

地球红外辐射热流可表示为[15]：

(3)

地球反照热流可以采用简化方法计算[15]：

(4)

式中：Re为地球半径；h为轨道高度；φ为θ0、δe的函数；γs为日地连线与微元表面地心连线的夹角。θ0和δe的定义见图3， 可以采用文献[15]中的公式进行计算或通过查图获得。文献[15]的结果表明，地球红外辐射热流随着θ0的减小而减小，随着δe的减小而增大。

图3 θ0和δe的定义Fig.3 Definition of θ0 and δe

1.2.2点火段

对于中高轨道卫星，通常上面级点火段轨道高度超过18 000 km，因此地球红外辐射热流和地球反照热流均可忽略，仅需考虑太阳辐射热流。点火段卫星姿态示意图见图4。

根据点火段的卫星姿态，各个面的太阳辐射热流可表示为：

qX=Ssinβ

(5)

qZ=Scosβsin(Λ-f)

(6)

qY=Scosβcos(f-Λ)

(7)

式中:f为卫星位置真近点角，热流计算结果如果是负值则表示所在舱板的对板受照，且所在舱板太阳辐射为0。

图4 点火段卫星姿态示意图Fig.4 Satellite attitude during firing phase

由开普勒定理，可得到点火段卫星各个面的平均热流计算式：

(8)

式中:n为平均角速度，t1,t2分别为点火段开始和结束时间，E1,E2分别为点火段开始和结束时的偏近点角，g(i)表示点火段卫星第i面在轨受照函数，具体见式(5)～(7)。

将式(5)～(7)分别代入式(8)，并根据真近点角和偏近点角的关系，积分求得各个面点火段平均太阳辐射热流：

(9)

(10)

(11)

式中：

式中:e为轨道偏心率；f1、f2分别为点火段开始和结束时真近点角。

2 上面级轨道外热流影响因素分析

选取北斗三号中轨导航卫星作为计算实例，轨道倾角55°，飞行时间约12 100 s，其中滑行段11 000 s，点火段1 100 s。

2.1 阳光与轨道面夹角

根据1.2.2节的分析结果，β角对点火段各个面的平均太阳辐射热流有较大影响。考虑到导航卫星全天候发射可能，需要分析上面级在不同的太阳黄经和升交点赤经情况下的太阳方位。β角大小可由下式确定[15]：

sinβ= cosisinIsinΦ+sinisinΩcosΦ-

sinicosIcosΩsinΦ

(12)

式中:i为轨道倾角，Φ为太阳黄经，I为黄道面与赤道面夹角。

根据式(12)可以给出不同太阳黄经和升交点赤经条件下的β角，如图5和图6所示。从中可以看出，阳光与轨道面的最大夹角±78.5°，出现在夏至或冬至、升交点赤经180°时；阳光与轨道面的最小夹角0°，对任意的太阳黄经和升交点赤经均会出现。

图5 β角随太阳黄经的变化Fig.5 Variation of β with solar longitude

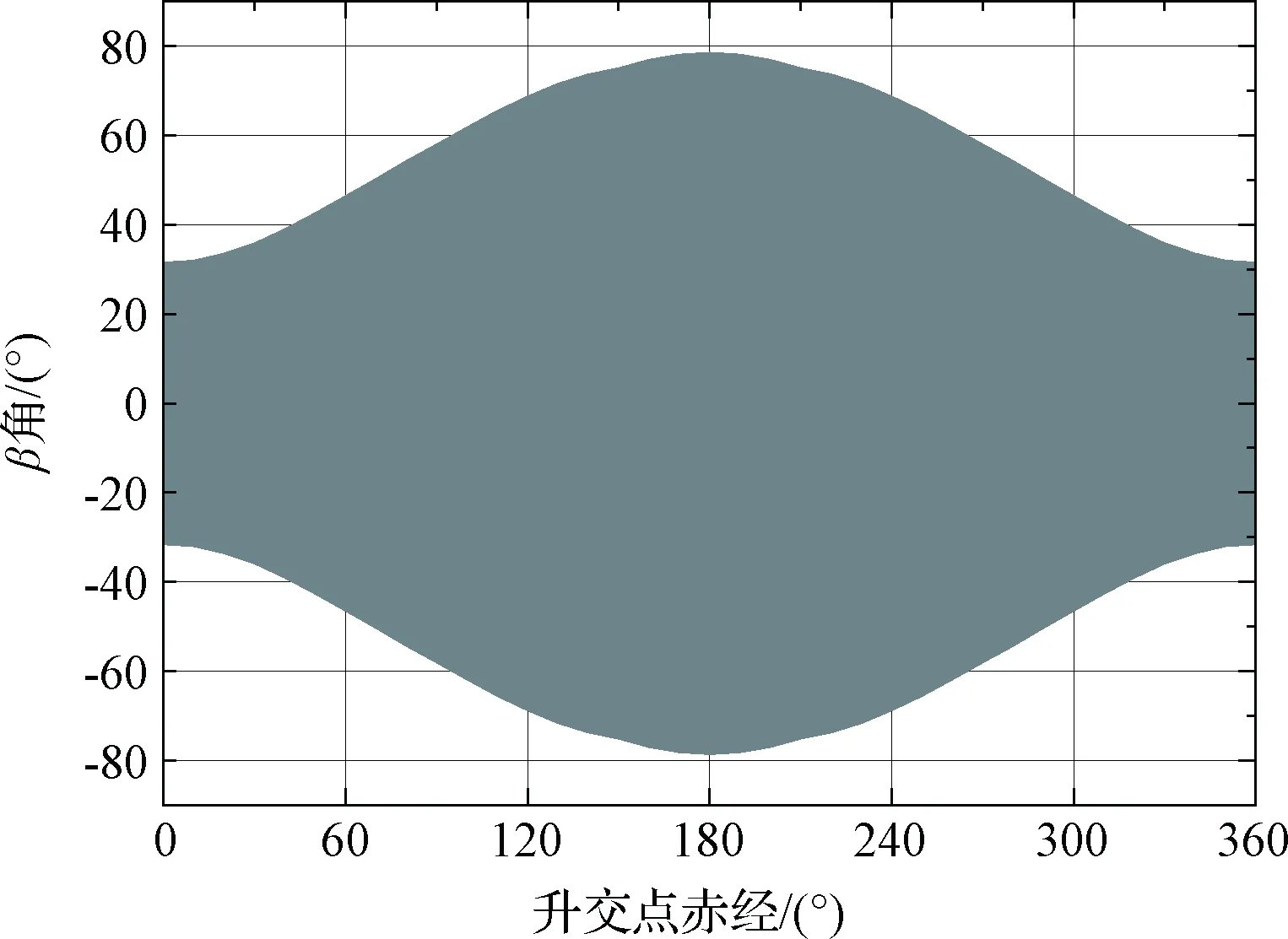
图6 β角随升交点赤经的变化Fig.6 Variation of β with right ascension of ascending node

2.2 阴影时间

椭圆轨道进入阴影的位置关系及临界阳光与轨道面夹角β0可分别表示为[16]：

(1+ecosf)2+λcos2βcos2(f-Λ)-λ=0

(13)

(14)

β0随会日点的变化见图7。从中可见，当会日点位于近地点时(Λ=0°)最小，约为13.0°，当会日点位于远地点时(Λ=180°)最大，约为75.8°。当会日点由近地点向远地点变化时，β0会越来越大。

图7 临界角β0随会日点的变化Fig.7 Variation of β0 with subsolar point

在给定β角和会日点Λ的前提下，进出阴影区的真近点角f1、f2可通过式(13)求解得到。

卫星在阴影区飞行时间可按下式计算[16]：

(15)

式中:M1、M2分别为进、出阴影平近点角，μ=398 600 Km3/s2，为地心引力常数。根据卫星进、出阴影的真近点角，可计算出相应的偏近点角和平近点角，进而计算出地影时间。

显然，最长阴影出现在阳光与轨道共面时，即：β=0°。对于封闭的椭圆轨道来说，其最长阴影出现在β=0°、Λ=0°时，如图8所示。对于非封闭的上面级椭圆轨道，最长阴影出现在β=0°且点火结束卫星正好出地影的情况，如图9所示。根据点火结束时的真近点角f2，利用式(13)可以计算出此时会日点Λ=-10.2°，对应的最长阴影时间约为5 558 s。图10给出了不同会日点条件下上面级轨道可能出现的最长阴影时间。

图8 封闭椭圆轨道最长阴影示意图Fig.8 Maximum eclipse of closed elliptical orbit

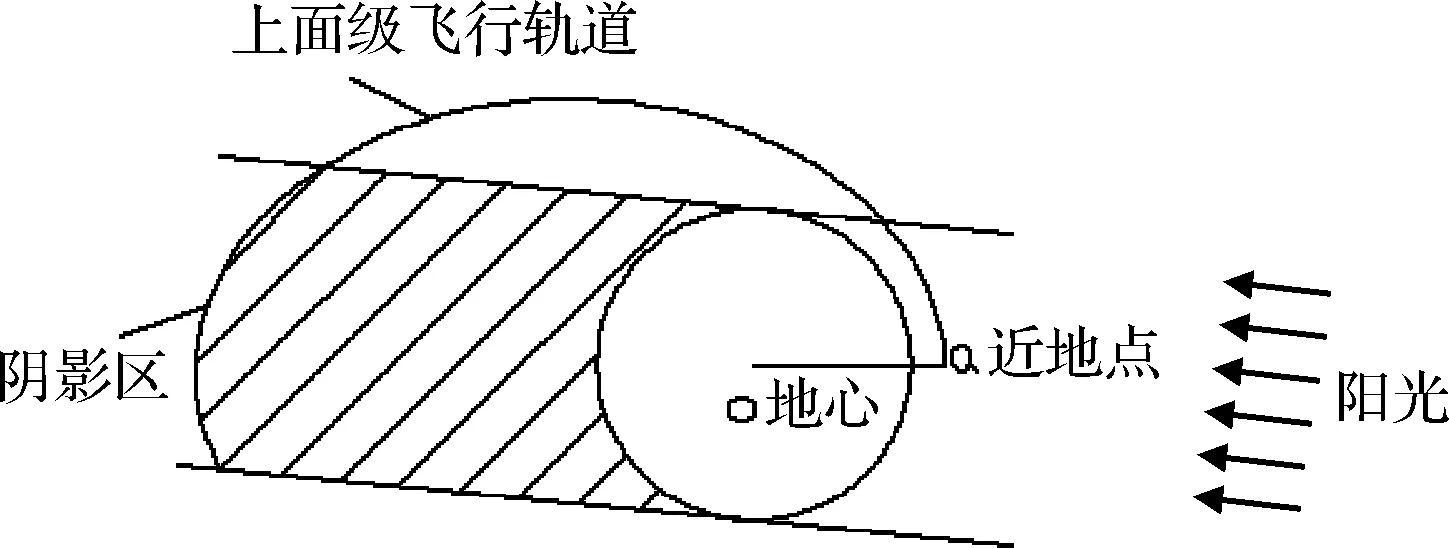
图9 上面级非封闭椭圆轨道最长阴影示意图Fig.9 Maximum eclipse of unclosed elliptical orbit

图10 不同会日点对应的最长阴影时间Fig.10 Maximum eclipse duration for different subsolar points

2.3 滑行段旋转角速度

如果滑行段旋转角速度过低，则会出现某一侧散热面长期受照的情况，在地球红外辐射和地球反照的共同作用下，有可能出现散热面温度不断升高的情况，因此，对旋转角速度的约束条件是：在该角速度下，散热面受照导致的设备温度升高不超过其工作温度上限。如前所述，中、高轨卫星散热面位于卫星的±Y、 +X(或-X)，由于每块舱板的热容、设备热耗均不相同，设备温度指标也各不相同，因此需要分别进行分析，本文给出了其中一块舱板(+X)的分析方法和结果，其它各个舱板可以采用相同的方法进行研究，最终综合各舱板的分析结果给出旋转角速度的约束条件。

为便于分析，近似认为+X散热面和其上设备温度一致并忽略舱内设备间的辐射换热，则有：

(16)

式中:αs、εh分别为散热面涂层的太阳吸收率和红外发射率；pi为单位面积散热面上的设备热耗；mc为单位面积舱板和设备热容。对某一确定的卫星而言，这几个量均可视为定值。通常卫星起飞时，部分部件的温度较高，初始阶段由于轨道高度较低，地球红外辐射和太阳反照相对较大，因此在最初的一段时间内散热面上吸收的外热流应该是在轨飞行最大的一段，由此选定如下计算条件：

1)旋转轴方位：选取旋转轴垂直于地心、日下点和初始时刻卫星位置组成的平面，滑行段后续飞行过程中旋转轴空间位置保持不变。此时ψs=90°，阳光与+Z轴垂直，由式(2)可知，滑行段散热面上太阳辐射热流最大。

2)初始时刻，选取+X面法线方向指向地心，此时δe=0°且轨道高度最低，+X面地球红外辐射热流最大。

3)选取Λ=90°，根据1)和2)确定的条件，初始时刻阳光将与+X面平行，随着飞行过程中绕+Z旋转，+X面与阳光的夹角变大，这样可以保证最初的半个旋转周期内+X面受照。

4)Λ=90°时，通过空间位置计算得到δe和β角的关系式如下：

δe=arccos(cos(ω′t)cosf-sin(ω′t)sinfcosβ)

(17)

式中:ω′为旋转角速度。上式对β求导可得到如下结论：当0≤ω′t<π时，|β|取最大值时δe有极小值。由1.2.1节中的结论可知，在最初的半个旋转周期内，当卫星飞行到某一轨道位置时(真近点角f)，选取β=±78.5°时，+X面的地球红外辐射热流相对选取其他β角时更大。

5)地球反照热流在散热面吸收热流中所占比例较小，不对其约束条件进行讨论。

按照上述1)～5)所确定的条件，以及本文算例选取的某一舱板OSR散热面和单位面积散热面上的设备热耗等参数，选取不同的旋转角速度，使用IDEAS-TMG热分析软件进行计算，散热面吸收外热流计算结果见图11。假定散热面初始温度35 ℃，计算得到不同的旋转角速度下散热面所能达到的最高温度，如图12所示。如果设备高温上限为45 ℃，则其旋转角速度不能低于0.0485°/s。采用相同的方法对其它各舱板进行分析，得到的旋转角速度约束条件均未超过0.0485°/s。因此，对于中轨导航卫星，滑行段的约束条件为：旋转角速度不能低于0.0485°/s。

图11 不同旋转角速度下散热面吸收总热流Fig.11 Total amount of absorbed heat flux for different rotational angular velocities

图12 不同旋转角速度下散热面及设备达到的最高温度Fig.12 Maximum temperature achieved for different rotational angular velocities

3 上面级轨道极端外热流工况分析

3.1 最小外热流工况分析

最小外热流工况应为最长阴影工况，如图9所示；同时在近地点至进影前的滑行段，ψs=0°或180°时，阳光直照卫星面+Z或-Z面，散热面不受照。

3.2 最大外热流工况分析

对于滑行段，由式(2)可知，散热面上周期平均太阳辐射热流仅取决于阳光与卫星+Z轴的夹角和太阳常数，当ψs=90°时，阳光与+Z轴垂直，散热面周期平均太阳辐射热流最大。

对于点火段，不同的轨道参数下各个面的受照情况相差较大。由式(9)可知，点火段卫星X面太阳辐射平均热流主要取决于β角，β角越大，X面的太阳辐射平均热流越大。对于本文选取的实例，当β=78.5°时，为卫星+X面的最大外热流工况；当β=-78.5°时，为卫星-X面的最大外热流工况。

(18)

由此式求得+Y面太阳辐平均辐射热流取极大值时对应的会日点Λ′。根据本文算例点火段开始和结束时对应的真近点角，由式(10)求得A、B的值，从而得到Λ′=180.14°。由于-Y面和+Y面相对，因此理论上-Y面点火段太阳平均辐射热流值极值应出现在时β=0°、Λ′=0.14°，但此时点火段会出现阴影，因此需要找到该会日点对应的临界β角以避开阴影，由式(14)计算得到：β0=13.0°。

3.3 极端外热流工况及计算结果

依据上述分析，选取上面级轨道极端热流工况如表1所示。

外热流计算结果见表2。从中可以看出，最小外热流工况各个面到达的太阳热流和地球红外热流分别在5.8～6.6W/m2和9.9～11.4 W/m2之间，量级很小，可以采取调整滑行段阳光和旋转轴的夹角以及限制发射窗口以避开长地影时间的方法来增大散热面外热流。最大外热流工况各个面到达的最大太阳热流和对应的地球红外热流分别在635.6～674.4 W/m2和12.7～20.9 W/m2之间，可以采取调整滑行段阳光和旋转轴的夹角以及提高旋转角速度的方法来减小散热面外热流。

表1 极端外热流工况Table 1 Extreme external heat flux cases

表2 极端工况外热流计算结果Table 2 Results of external heat flux for extreme cases

4 外热流分析结果正确性验证

外热流分析结果可以通过计算温度和在轨飞行温度的比对进行验证。由式(16)可知，卫星温度取决于外热流、散热面的太阳吸收率和红外发射率、舱板及设备热容以及设备热耗，对于确定卫星的某一舱板，后两项为固定值，第二项根据多颗中、高轨卫星在轨飞行的数据积累，也可以得到较为准确的数据，因此卫星计算温度主要取决于外热流分析结果是否正确。如果卫星温度计算结果和在轨温度数据较为吻合，则可证明外热流分析结果的正确性。具体方法如下：根据卫星发射的轨道参数，采用本文所述的方法计算得到β角和会日点，再按照1.2节所述方法计算得到滑行段和点火段的外热流，代入计算模型计算得到舱板温度，将该温度和在轨飞行数据进行比较。

选取北斗三号中轨卫星两次发射的轨道参数，计算得到的β角和会日点，如表3所示。图13、图14分别为滑行段和点火段计算温度和在轨温度数据的比对结果，从中可以看出，同一时刻计算温度和在轨温度相差不超过5 ℃，表明本文外热流分析结果和分析方法正确。

表3 北斗三号中轨卫星发射工况Table 3 Launch cases of BDS-3

图13 工况2滑行段计算温度和在轨温度比较Fig.13 Comparing of calculation temperature with data in orbit during coast phase at case 2

图14 工况1和工况2点火段计算温度和在轨温度比较Fig.14 Comparing of calculation temperature with data in orbit during firing phase at case1 and case 2

5 结束语

本文针对上面级发射轨道的特点，给出了上面级轨道滑行段和点火段瞬态热流和平均热流的计算公式。结合北斗三号中轨导航卫星，分析了上面级发射阶段影响卫星外热流的主要因素，给出了β角随太阳黄经和升交点赤经的变化关系，以及最长阴影时间、滑行段旋转角速度约束条件的分析方法。在此基础上确定了各个面的极端外热流工况并进行了分析计算。结果表明：

1)滑行段外热流大小主要取决于慢旋角速度以及阳光与旋转轴的夹角；

2)点火段太阳辐射热流平均值取决于β角和会日点；

3)地影对外热流影响较大，可以通过选择适当的发射窗口，避开长地影；

4)滑行段上面级慢旋角速度过小会带来设备温度超上限的风险，需要对最小旋转角速度进行约束。