固体运载火箭抗强电磁脉冲优化设计方法
2018-11-08龙中权付继伟
龙中权,赵 民,付继伟,陈 曦,齐 欢
(1. 北京宇航系统工程研究所,北京 100076;2. 中国运载火箭技术研究院,北京 100076)
0 引 言
雷电电磁脉冲(Electromagnetic pulse,EMP)及静电等强电磁脉冲对火箭箭上电子电气设备的危害一直备受关注,火箭箭上电气系统的抗强电磁脉冲指标是衡量火箭总体性能的重要依据。强电磁脉冲是一种瞬时电磁辐射,耦合进入箭上电气系统后,会对系统的硬件、软件及电路接口等造成严重地影响,可能导致整个系统工作异常,无法完成预定任务[1-2]。
目前,国内外对于固体火箭系统强电磁脉冲工程防护方法主要有屏蔽、滤波、限幅和接地等[3-5]。在以往相关文献中,对各种电子电气系统的强电磁脉冲防护研究较为透彻,但是很少关注系统进行防护设计后给火箭带来的质量增量[6]。由于箭上对质量控制要求较高,如果对箭上所有系统按照严格指标进行抗强电磁脉冲加固设计,虽然可以达到防护指标要求,但是会给箭上带来巨大的质量增量,这对火箭箭体结构、发动机等提出了更高的要求。实际工程中,发动机的性能参数往往已经被最大利用,没有过多设计余量,因此,为了综合考虑火箭的抗强电磁脉冲加固设计与火箭总体设计的关系,需要寻求箭上系统抗强电磁脉冲指标与质量增量之间的平衡。
本文选取箭上典型电气系统为研究对象,针对强电磁脉冲对箭上敏感设备的干扰,建立了典型电气系统基于最小质量增量的抗强电磁脉冲加固优化模型,采用模拟退火优化算法计算得到箭上典型系统抗强电磁脉冲干扰指标与质量增量的关系,为箭上电气系统抗强电磁脉冲加固设计指标分配方法提供了参考依据。
1 箭上系统抗强电磁脉冲优化模型
火箭起飞以后,箭上的电子电气系统失去了壳体的有效防护,直接面临大气中强电磁脉冲的威胁。强电磁脉冲对箭上敏感设备的影响主要包括传导干扰和辐射干扰[7]。
1.1 典型系统传导干扰防护设计模型
火箭在飞行过程中,强电磁脉冲以传导方式进入敏感设备的途径主要包括脱插插座以及线缆。强电磁脉冲经过脱插的插孔,会在与脱插连接的线缆芯线上产生感应电流;同时,线缆的屏蔽层在强电磁脉冲的作用下,会产生脉冲感应皮电流。图1为电磁脉冲耦合进入敏感设备的示意图。
1.1.1脱插
1)脱插感应电流分析:
火箭在飞行过程中,当级间分离后,脱插的插座直接暴露在强电磁脉冲的威胁下,极易受到强电磁脉冲的干扰。按照最严苛的考核条件(强电磁脉冲电场方向与插座孔的轴向方向平行),与之相连的线缆芯线上形成的感应电流峰值达到最大:
I1=Itc
(1)
2)脱插加固后质量增量模型:
工程应用中,脱插的加固主要针对脱插闭合状态下的加固设计,而本文主要考虑脱插分离之后的电磁干扰。所以这里不考虑脱插进行抗强电磁脉冲加固设计,从而由脱插加固设计引起的质量增量为:
mtc=0
(2)
1.1.2线缆
1)线缆屏蔽层感应电流分析:
强电磁脉冲在火箭尾段线缆屏蔽层上的感应电流峰值大小与多种因素有关,包括强电磁脉冲的入射方向、极化方向以及线缆的长度等。按照最严苛的考核条件,可以得到箭体尾段设备端口处的线缆屏蔽层感应电流峰值为Ixl,即:
I2′=Ixl
(3)
2)线缆加固质量增量模型:
线缆抗强电磁脉冲加固的最常用方法是在外面包裹一定厚度的屏蔽材料,屏蔽层直接与地相连。线缆屏蔽措施包含多种方式,这里重点研究单层编织(sb)、双层编织(db)以及铜箔编织(cb)三种屏蔽方式带来的质量增量。由于加固手段如上所述是有限的几种,因此,目标函数是阶梯函数。
在0~30 MHz频率范围,线缆的加固手段B与转移阻抗的关系[8]:ZT(sb)=0.1 Ω/m,ZT(db)=0.003 Ω/m,ZT(cb)=0.001 Ω/m。从而可以得到线缆的质量与加固方式的对应函数关系:
(4)
且:
I2i=(IxlZTiLcable)/Zd,i=0,1,2,3
(5)
式中:mcable(B)/Lcable表示单位长度电缆加固重量代价,B为加固手段,d为电缆直径,Lcable代表线缆的长度,ki是表征加固方式带来的质量增量的常数,可以根据不同类型线缆做相应的调整,Zd为敏感设备端口的输入阻抗。
1.1.3端口抑制电路
为了防止大电流进入箭上敏感设备,一种有效的措施是在设备端口处使用电压/电流抑制器。瞬态电压抑制二极管(Transient voltage suppressors, TVS)是一种专门用于抑制浪涌的齐纳二极管。TVS二极管具有响应快、瞬态功率大、箝位电压容易控制、体积小等优点,目前已在实际工程中得到了广泛的应用。
1)TVS管输出电流分析[9]
单向TVS二极管的电流-电压特性曲线其正向特性与普通二极管相同,反向特性为典型的PN结雪崩器件。根据TVS二极管的反向击穿特性,可以得到流经敏感设备端口的电流:
(6)
式中:Vc为最大箝位电压,Zd为端口输入阻抗。
2)抑制电路质量增量模型
在箭上敏感设备的端口增加瞬态抑制电路,给箭上带来的质量增量包括两个方面:抑制电路本身的重量以及由于使用抑制电路导致设备壳体体积增大带来的壳体质量增量。
抑制电路的重量:
myz1=mtvs
(7)
壳体质量增量:
(8)
从而,由端口抑制电路带来的质量为:
myz=myz1+mkt
(9)
综合上述分析可以得到设备抑制端口电路的质量增量模型为:
(1)若端口不使用TVS管:
(10)
(2)若端口使用TVS管:
(11)
1.1.4传导干扰优化设计目标函数及约束条件
综合上述分析,强电磁脉冲以传导方式干扰敏感设备时,为了平衡敏感设备端口电流大小与质量增量之间的关系,建立质量增量最小的优化模型如下:
目标函数选取为强电磁脉冲传导干扰给箭上带来的质量增量,目标函数极小值的形式可以表示为:
min{mchd}=min{mtc+mcable+myz,tvs}
(12)
其约束条件为:
I1+I2+I3 (13) 其中,IYQ为进入敏感设备端口的电流指标要求,根据实际敏感设备端口能够承受的最大感应电流确定。 强电磁脉冲辐射耦合进入敏感设备有多种途径,主要包括壳体、屏蔽门、透光玻璃以及壳体上缝隙、通风孔等,如图2所示。一般来说,用衰减量来衡量箭上系统抗强电磁脉冲辐射效应的指标。 1.2.1壳体质量与衰减量的理论设计模型 目前,箭上设备的壳体材料主要包括金属材料以及碳纤维复合材料,碳纤维复合材料相对金属材料质量较小,并且具有极好的振动阻尼性、抗疲劳等性能,所以这里选取碳纤维复合材料作为设备壳体材料的研究对象。碳纤维壳体质量增量与衰减量(A)的关系为[10]: (14) 式中:ρkt,dkt分别表示碳纤维的密度和厚度,这里dkt取1 mm,Skt表示壳体碳纤维部分的面积,T是与材料本身屏蔽性能有关的屏蔽效果特征参数,表明碳纤维壳体的厚度每提高一倍,壳体的衰减量可以增加TdB。 1.2.2缝隙质量增量与衰减量的理论设计模型 强电磁脉冲容易通过设备壳体的缝隙耦合进入敏感设备。对于适中的屏蔽要求(A≤60 dB),使用较廉价的导电泡棉,对于较高要求(A≤80 dB),则需要使用导电胶条或者指篝弹片等。导电泡棉和导电胶条相对于舱体本身来说,重量很小,可以忽略。因此,缝隙的抗核加固设计与重量的关系为: (15) 式中:At表示所采用的措施所能达到的最高衰减量,对于导电泡棉At取60 dB,而对于导电橡胶或者指篝弹片At取80 dB,其它情况类似。 1.2.3通风孔 对于有通风散热要求的壳体,需要设计合适的波导窗,相关文献表明[11],波导窗的厚度与衰减量成线性关系,所以质量增量与衰减量的关系为: mtb(Atb)=AtbmtbStb (16) 式中:mtb为实现每dB衰减量的波导窗单位面积重量,Stb为波导窗的面积。 1.2.4辐射干扰优化设计目标函数与约束条件 综合上述分析,强电磁脉冲以辐射方式干扰敏感设备时,为了平衡箭上敏感设备的衰减量指标与质量增量指标之间的关系,建立以质量增量最小的优化模型,目标函数选取为强电磁脉冲辐射干扰给箭上带来的质量增量,目标函数极小值的形式可以表示为: min{mfs}=min{mkt+mmf+mtb} (17) 约束条件为设备壳体的综合衰减量,使综合衰减量达到设计指标要求: A≥AYQ (18) 式中:A=-10lg(10-Akt/10+10-Amf/10+10-Atb/10),AYQ为设备壳体需要达到的总衰减量指标,根据壳体内设备能够承受的辐射干扰阈值来确定。 通过分析火箭在飞行过程中的强电磁脉冲环境,建立了传导干扰以及辐射干扰模型,根据耦合进入敏感设备端口的传导电流峰值指标以及辐射效应的衰减量指标,结合文中建立的模型及优化方法,可以计算得到箭上满足抗强电磁脉冲指标的最小质量增量: Δm= min{mkt+mmf+mtb}+min{mtc+ mcable+myz,tvs} (19) 且满足约束条件: (20) 本文建立了典型系统强电磁脉冲防护与质量这两个学科之间桥梁,从而为将强电磁脉冲加固设计与火箭总体参数设计结合研究提供了有力支撑,如图3所示。 2.1.1模型数据 本文考虑箭上典型系统的强电磁脉冲环境的波形为双指数波,其上升沿为2.5 ns,半宽高为23 ns。 1)对于脱插: 当脱插在上述双指数脉冲波辐照下,相关试验结果表明,在与其相连的电缆芯线上产生的感应电流最大峰值约为0.1138 A,由式(1)可以得到:I1=Itc=0.1138 A。 2)对于线缆: 根据线缆厂家提供的数据,代入式(4)可以得到:k0=38.8,k1=43.8,k2=52.5,k3=59.4。 考虑规格为98芯0.35 mm2的线缆,线缆的直径为16 mm,按照质量平均分配,可以得到火箭各级的电缆等效长度。经计算,I级电缆网总等效长度为80 m,仪器舱电缆网总等效长度为60 m。根据有关实验结果,按照最严苛的考核条件,箭上尾段线缆屏蔽层上感应电流的最大峰值约为30.77 A;而仪器舱里的线缆,其最大的感应电流峰值约为57.46 A。 综合上述分析,可以得到I级线缆和仪器舱线缆质量增量与芯线电流的关系: I级线缆: (21) 仪器舱线缆: (22) 对于端口抑制器件,根据线缆芯线电流分布, I级可选用SY5637型号TVS管。假设敏感设备端口为50 Ω匹配负载,则在TVS管未击穿之前,允许流入敏感设备端口的电流最大值为: (23) 敏感设备接入TVS管之后,为了避免TVS管被烧毁,由于其箝位电压为22 V,所以,允许流过敏感设备端口的最大电流为0.44 A。 根据调研结果,代入参数到式(8)、式(9),可得: myz1=1.5×10-3kg (24) (25) 这里考虑尺寸为20 cm×20 cm×20 cm的碳纤维复合材料的壳体,假设每增加一个TVS管,其体积的变化引起的设备壳体体积同比例增加。从而,每使用一个TVS管,带来的质量增量为myz=mzs+mfj=0.00518 kg。所以其质量变化与电流的关系为:若端口不使用TVS管,则myztvs(I)=0,I3=0;若端口使用TVS管,则对于I级尾段线缆,myz=0.51 kg,VR/Zd=0.3 A,Vc/Zd=0.44 A;对于仪器舱,由于包含精密元器件较多,为保证6 dB余量,故选用功率为3000 W的3KP13型号TVS管,从而myz=2.007 kg,VR/Zd=0.26 A,Vc/Zd=0.45 A。 将上述参数代入箭上典型系统的强电磁脉冲传导干扰防护优化设计模型,如式(12)及式(13)所示,利用优化算法求解敏感设备抗强电磁脉冲指标与其带来的质量增量的关系。 2.1.2优化结果 模拟退火优化算法是一种随机算法,具有跳出局部最优点及运行时间短等多种优点,本文采用模拟退火算法对上述模型求解最优解,针对敏感设备端口能够承受不同幅度的峰值电流进行优化,初始温度为100 ℃,温度下降采用指数衰减的方式,温度下降到0.1 ℃时终止。优化结果如表1、表2所示。 表1 I级尾段典型系统强电磁脉冲防护优化结果Table 1 Optimized results of typical system’s EMP protection on the first stage of launch vehicle 以仪器舱为例,目标函数优化的收敛情况如图4、图5所示,选取IYQ=0.2A以及IYQ=5A进行说明。 从图4、图5可以看出,当电流指标为0.2 A时,迭代3次之后即找到最优解,端口电流为0.19 A,最小质量为21.32 kg;当电流指标为5 A时,端口电流为0.45 A,迭代8次之后找到最优解,最小质量为2.01 kg。 2.2.1模型数据 对于设备壳体,考虑尺寸为20 cm×20 cm×20 cm的碳纤维符合材料壳体,且ρkt=1.81×103kg/m3;对于波导窗,根据式(16)代入相关系数,得到波导窗强电磁脉冲防护设计的重量增量与衰减量的关系为: mtb(Atb)=0.02Atb (26) 将上述参数代入箭上典型系统的强电磁脉冲辐射干扰防护优化设计模型,如式(17)及式(18)所示,利用优化算法求解敏感设备抗强电磁脉冲指标与其带来的质量增量的关系。 2.2.2优化结果 采用模拟退火优化算法对上述模型求取最优解,针对敏感设备能够承受的强电磁脉冲辐射阈值对壳体、波导窗以及缝隙进行优化。初始温度为100 ℃,降温过程采用指数衰减的方式,降温系数取0.99,当温度下降到0.1 ℃时终止,迭代次数取1000次,优化的结果如表3、表4所示(精度为0.1 dB)。 目标函数优化收敛情况如图6、图7所示,选取使用导电胶条AYQ=20 dB以及AYQ=70 dB为例进行说明。 从图6、图7可以看出,当衰减量指标为20 dB时,迭代46次之后即可找到最优解,最小质量为0.772 kg,当衰减量指标为70 dB时,迭代479次之后即可找到最优解,最小质量为43.130 kg,此时壳体的衰减量为71.1 dB,波导窗的衰减量为80.0 dB,缝隙处需要达到的衰减量为79.7 dB。 表3 辐射干扰优化结果(使用导电胶条)Table 3 Optimized results of radiation interference of typical system’s EMP protection using conductive rubber 表4 辐射干扰优化结果(使用导电泡棉)Table 4 Optimized results of radiation interference of typical system’s EMP protection using gasket 1)对于敏感设备强电磁脉冲的传导干扰: (1)对于I级尾段线缆,若设备对强电磁脉冲的感应电流要求较低(IYQ≤32 A),则线缆可以不采取加固措施,此时对火箭来说没有任何质量增量;若设备对强电磁脉冲的感应电流较为敏感(IYQ≤0.2 A),则线缆需要使用铜箔进行屏蔽,质量增量为23.99 kg。 (2)若为中等要求(IYQ≤0.5 A),则线缆可以不做任何屏蔽,在端口使用TVS管即可;对于I级,TVS管能够承受高达68 A的瞬时脉冲电流,对于分导级线缆,TVS管能够承受高达126 A,而流经设备端口的电流不超过0.5 A,可以达到设计要求。 (3)对于仪器舱的精密设备,若对端口电流要求较高(IYQ≤0.2 A),线缆则需要使用铜箔进行屏蔽,不需要在端口加抑制器件,其质量增量为21.32 kg。 2)对于敏感设备强电磁脉冲的辐射干扰: (1)缝隙处由于加固带来的质量代价较小,应该使用导电泡棉或者导电胶条进行防护。 (2)从表4的优化结果可以看出,为了使质量增量最小,应首先采取加固质量代价小的措施进行加固,如导电泡棉。 (3)随着敏感设备对强电磁脉冲衰减量指标的逐渐提高,由加固带来的质量代价也越来越大,所以,在实际工程中,应当权衡衰减量与质量增量的关系。 强电磁脉冲对固体火箭箭上电气电子设备的威胁不容忽视,箭上电气系统的抗强电磁脉冲防护一直是研究的热点。箭上电气电子设备进行强电磁脉冲防护设计过程中,在考虑敏感设备抗强电磁脉冲加固指标的同时,要关注由强电磁脉冲防护设计给箭上带来的质量增量,火箭质量的增加对火箭结构、发动机性能等提出了更高的挑战。本文分析了火箭在飞行过程中的强电磁脉冲环境,研究了箭上典型关键系统的强电磁脉冲耦合途径,重点研究了箭上敏感设备抗强电磁脉冲加固设计与其给箭上带来的质量增量关系,建立了箭上敏感设备抗强电磁脉冲优化设计模型,采用了模拟退火算法进行优化计算,得到了箭上敏感设备抗强电磁脉冲加固优化设计方案,为箭上电气系统的多种抗强电磁脉冲加固方案与质量增量提供了一种平衡选取方法,为火箭的强电磁脉冲防护融入火箭总体小回路设计研究提供了有益的参考依据。1.2 辐射干扰防护优化设计模型
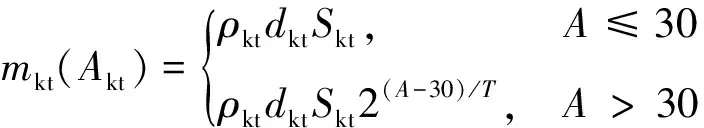

1.3 火箭箭上典型系统抗强电磁脉冲加固优化设计模型
2 实例分析
2.1 传导干扰优化设计

2.2 辐射干扰优化设计


2.3 结果分析
3 结束语
