双黑洞合并面积增量及放能率

李宝霖， 颜 骏

（1.青岛工学院基础教育学院，山东青岛266300； 2.四川师范大学物理与电子工程学院，四川成都610066）

黑洞是广义相对论引力理论预言的一种大质量恒星坍塌后的天体.对于是否含角动量及电荷又可分为不同类型的黑洞.1916年Schwarzschild首次得到广义相对论的球对称真空解（Schwarzschild黑洞），不久Reissner与Nordstrom得到了静态带电黑洞解（Reissner-Nordstrom黑洞）.20世纪60年代，文献［1-2］获得了广义相对论中的转动黑洞解（Kerr黑洞）及带电转动黑洞解（Kerr-Newman黑洞）.由于黑洞的“无毛定理”，我们只能观测到质量、角动量和电荷3种信息［3-8］，这对直接通过观测验证黑洞的存在带来困难.目前人们正积极寻找和证实黑洞这一神秘天体存在的证据.

1971年，在“宇宙监督假设”与强能量条件下，Hawking证明了黑洞的面积定理，即黑洞面积永不减小［9］.1973 年，Bekenstein［10］提出黑洞熵正比于外视界面积.对黑洞面积的研究可以增进对黑洞熵的认识.文献［11-12］对黑洞的表面积及熵进行了研究，结果满足面积定理.文献［13-14］研究了极端黑洞的熵，指出极端条件下黑洞的熵为零，但并没有消失，而是转移到了其他的高维空间.

2016年，文献［15-16］2次公布观测到双黑洞合并产生的引力波事件.黑洞这一神秘天体也逐渐为大家所熟悉，然而对双黑洞合并的研究并未引起重视.刘辽等［17］研究了2个 Schwarzschild黑洞合并的面积增量及放能率.然而对其他同种类型黑洞及不同种类型黑洞之间合并的研究尚未提上日程.

对双黑洞合并面积增量及放能率的研究，不仅可以进一步为天文观测提供理论依据，还可能为鉴别不同类型黑洞及引力理论提供一种新的研究思路.本文将研究 Schwarzschild、Reissner-Nordstrom、Kerr及Kerr-Newman 4种黑洞之间同种及不同种黑洞合并，通过计算并比较各类黑洞合并面积增量及放能率的大小，分析角动量以及电荷对其的影响，并讨论其物理意义.

1 双黑洞合并的面积增量

对于一个质量为M，角动量为J，带电量为Q的黑洞，其视界（或外视界）面积为

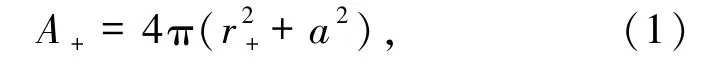
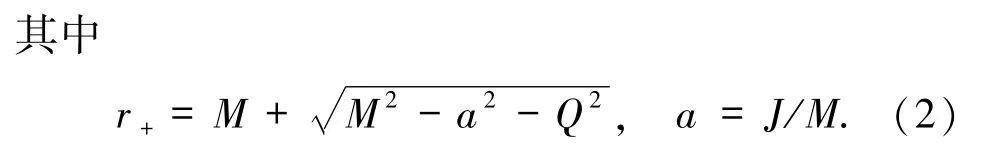
假设合并前2个黑洞的面积分别为A1、A2，合并后的大黑洞面积为A，则面积增量为

即黑洞表面积在顺时方向永不减少，这与热力学孤立系统中熵增原理一致.根据面积定理可知，2个黑洞要合并为一个黑洞，合并后的黑洞面积A不能比原来2个黑洞的面积和A1+A2小.此前刘辽等［17］讨论了2个 Schwarzschild黑洞合并（S-S型），其质量分别为M1、M2，得出合并后的面积增量为

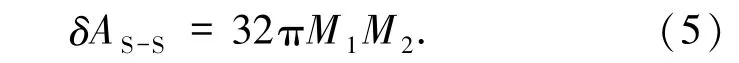
首先分析角动量对合并后面积增量的影响.若是一个Schwarzschild黑洞与一个Kerr黑洞合并（S-K 型），质量分别为 M1、M2，Kerr黑洞角动量为J2.可知原子黑洞的面积分别为

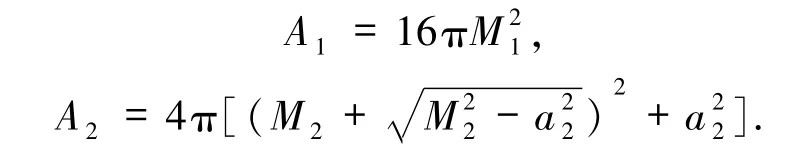
当无能量损失时面积增量最大，即M＝M1+M2，J＝J2，代入（1）式得合并后外视界面积为

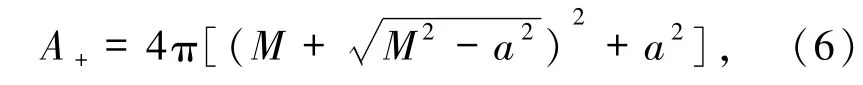
其中 a＝J2／M.

一般情况黑洞质量M≫a，因此可把a当作微扰项.对上式线性微扰展开可得

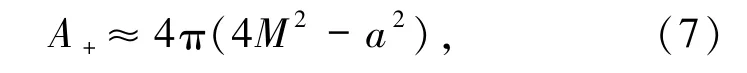
由（3）式可求得面积增量

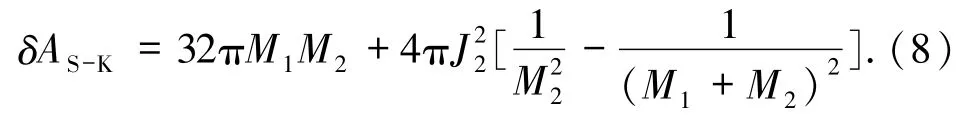
（8）式等号右边第二项大于零，因此S-K型黑洞合并的面积增量大于S-S型黑洞合并的面积增量 δAS-S.

若是2个Kerr黑洞合并（K-K型），质量分别为 M1、M2，角动量分别为 J1、J2.此时 2 个子黑洞的面积分别为

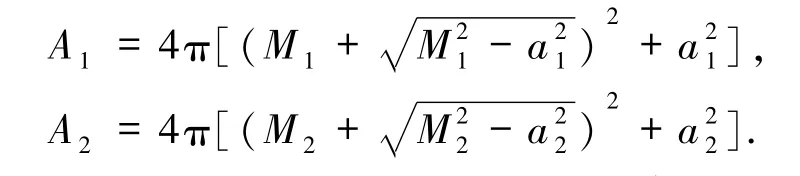
同样，在无能量损失时面积增量最大，代入（1）式得合并后外视界面积为

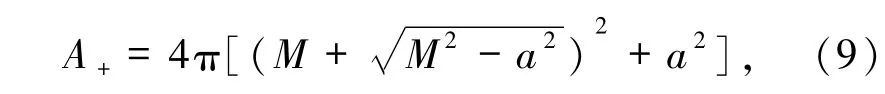
此时，M ＝ M1+M2，J＝ J1+J2.

采用线性微扰展开，同样可得K-K型黑洞合并的最大面积增量为

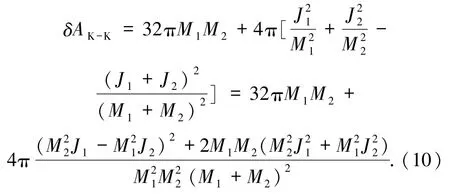
大于S-S型黑洞合并的面积增量δAS-S与K-K型同样.由此可见，由于角动量的存在，虽然会使原子黑洞的外视界面积减小（见（1）式），然而却会增大合并后的面积增量.

对于S-K型黑洞合并与K-K型黑洞合并面积增量的比较，可令

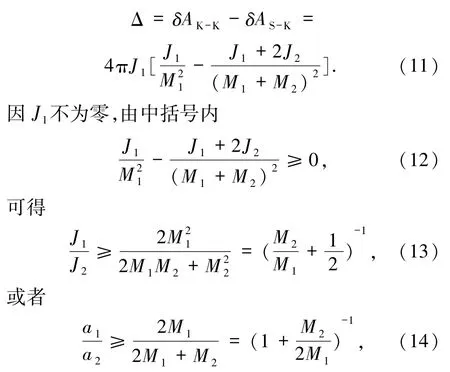
此时δAK-K≥δAS-K，即K-K型黑洞合并面积增量大于或等于S-K型黑洞合并面积增量；反之若

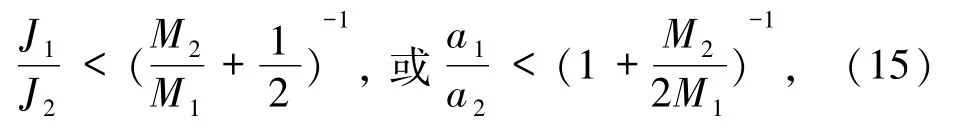
则K-K型黑洞合并面积增量小于S-K型黑洞合并面积增量.可见对于这两种黑洞面积增量的比较不仅涉及到角动量，还与本身质量比有关.

下面考虑电荷对面积增量的影响.首先对于2个Reissner-Nordstrom黑洞合并（RN-RN型），质量分别为 M1、M2，带电荷分别为 Q1、Q2.此时 2 个子黑洞的面积分别为：

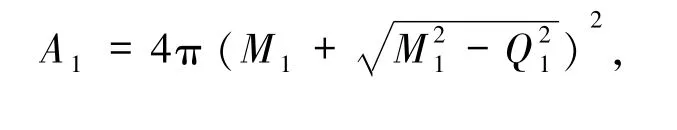
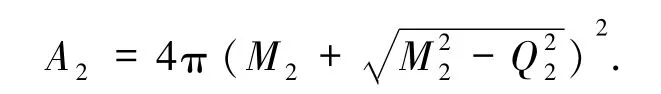
同样在无能量损失时面积增量最大，代入（1）式得合并后外视界面积为

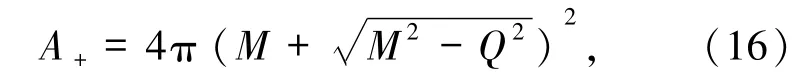
此时，M ＝M1+M2，Q ＝Q1+Q2.

一般情况M≫Q，采用线性微扰展开，同样可得RN-RN型黑洞合并的最大面积增量

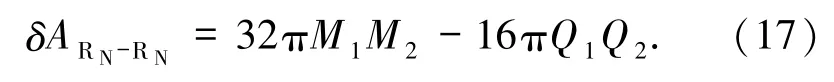
比S-S型黑洞合并的面积增量δAS-S小（若Q1、Q2为同种电荷），比S-S型黑洞合并的面积增量δAS-S大（若 Q1、Q2为异种电荷）.电荷本身会减小黑洞的表面积，但两子黑洞若是带异种电荷，则合并后面积增量会增大，这可能是异种电荷相互抵消的缘故，因此对面积的影响也相应减弱.可见同种电荷的存在会使合并后面积增量变小，如果是带两种异种电荷，反而会使合并后的面积增量变大.然而我们注意到，采用线性微扰展开后，电荷对面积增量的影响表现为2个电量的乘积项，也就意味着如果只有一方带电，那么这一项为零，即单方带电对合并后的面积增量没有影响.由此可推论，SRN型黑洞合并的面积增量应与S-S型一致，KKN型（KN为 Kerr-Newman）黑洞合并应与 K-K型相同，实际经过具体计算也可得出这样的结论.

对于Reissner-Nordstrom黑洞与Kerr-Newman黑洞合并（RN-KN型），质量分别为 M1、M2，带电荷分别为Q1、Q2，Kerr-Newman黑洞角动量为J2.此时2个子黑洞的面积分别为：

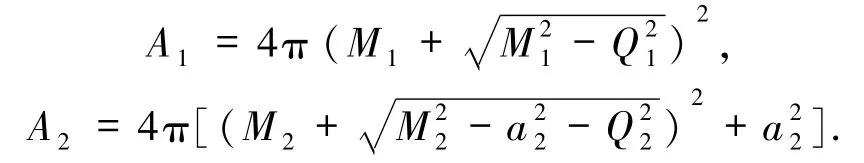
同样在无能量损失时面积增量最大，代入（1）式得合并后外视界面积

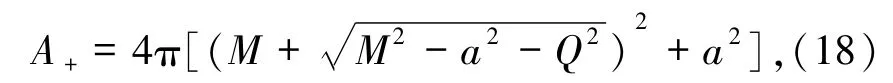
此时，M ＝M1+M2，Q ＝Q1+Q2，J＝ J2.

线性微扰展开后，同样可得RN-KN型黑洞合并的最大面积增量为

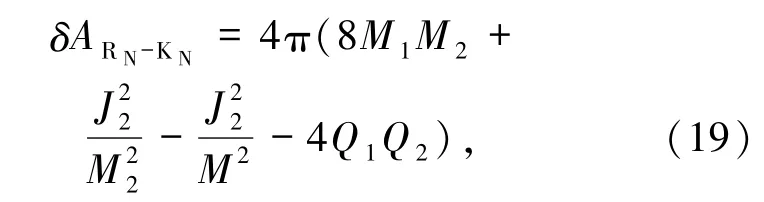
比 δAS-K小（若 Q1、Q2为同种电荷），比 δAS-K大（若Q1、Q2为异种电荷）.与S-S型黑洞合并的面积增量 δAS-S比较，若

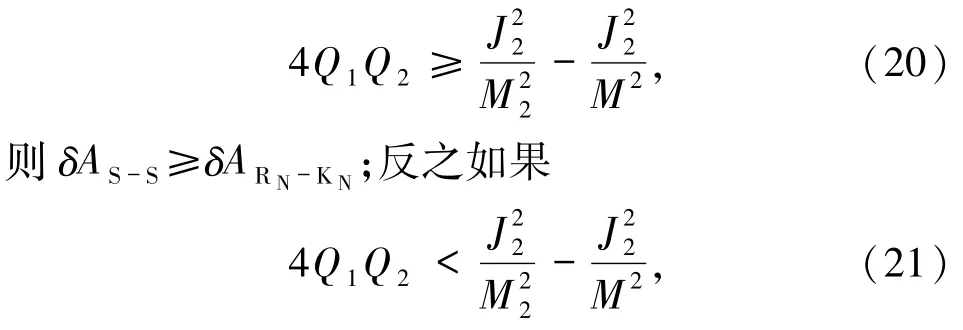
则 δAS-S＜ δARN-KN.

对于2个Kerr-Newman黑洞合并（KN-KN型），质量分别为 M1、M2，带电荷分别为 Q1、Q2，角动量分别为J1、J2.此时2个子黑洞的面积分别为：

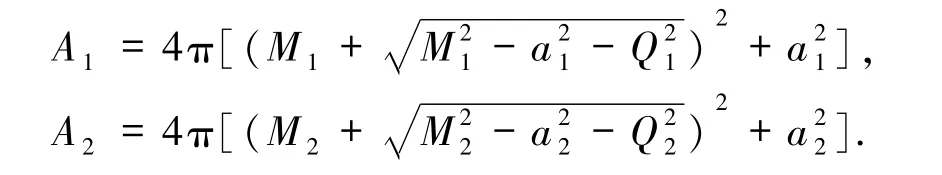
同样在无能量损失时面积增量最大，代入（1）式得合并后外视界面积为

比 δAK-K小（若 Q1、Q2为同种电荷），比 δAK-K大（若 Q1、Q2为异种电荷）.然而与 δAS-S比较，同样，若

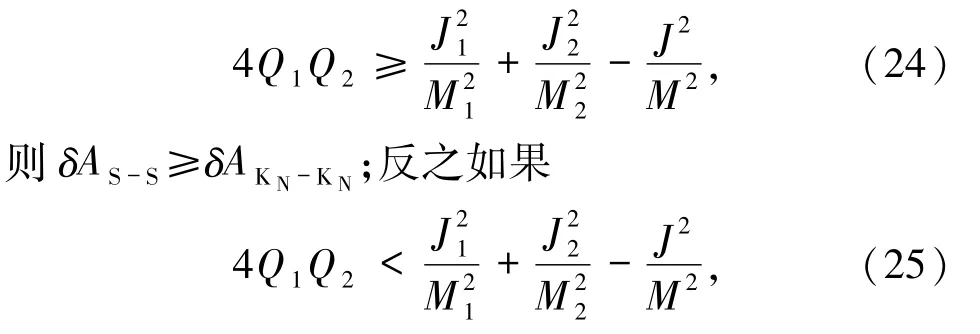
则 δAS-S＜ δAKN-KN.

综上所述，对于双黑洞合并后的面积增量的大小可大致排列如下：

另一方面，由面积定理也可得RN-KN型及KN-KN型黑洞合并原子黑洞带电的临界条件分别为：

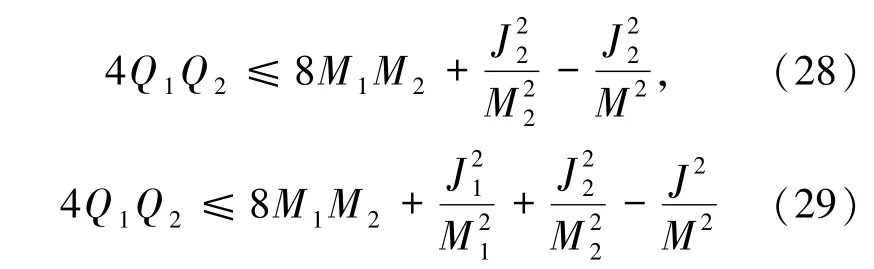
为带同种电荷情况，带异种电荷则不存在此临界条件.

2 双黑洞合并的放能率

假设合并前2个黑洞的质量分别为M1、M2，合并后的大黑洞质量为M，同时假设合并后电荷及角动量无损失，则合并后的放能率

其中 δM ＝M1+M2-M.文献［17］讨论了 2个Schwarzschild黑洞合并（S-S型），其质量分别为M1、M2，由面积定理，可得最大放能率

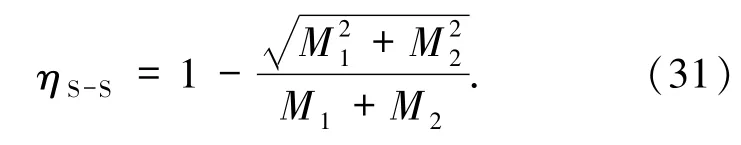
当2个子黑洞的质量相等时取极大值，由此得放能率 η≤1-

首先依然分析角动量对最大放能率的影响.若是一个Schwarzschild黑洞与一个Kerr黑洞合并（S-K 型），质量分别为 M1、M2，Kerr黑洞角动量为J2，面积分别为A1、A2.合并成一个大黑洞后质量为M＝M1+M2，面积为A，放出能量为δM，由面积定理可得δM取极大值的条件为

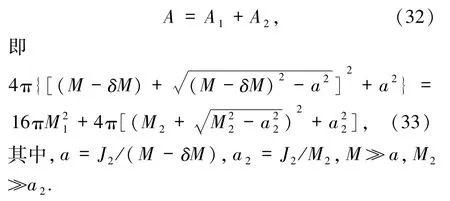
对上式线性微扰展开可求得S-K型黑洞合并理论可达到的最大能量损失为

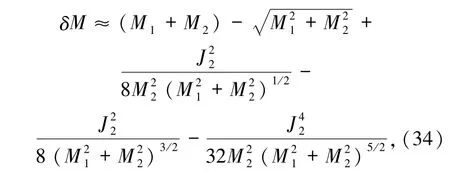
其中已略去高阶微扰项.实际上等式右边最后一项也可看作高阶小量，因此仅保留前面4项，即

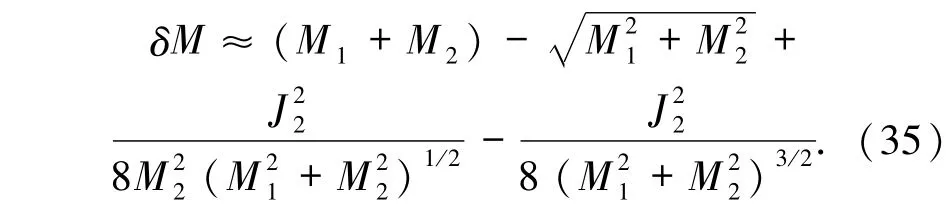
由（30）式可求得S-K型黑洞合并的最大放能率为

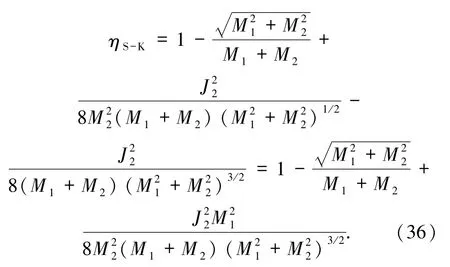
与（31）式比较，上式右边最后一项大于零，因此S-K型黑洞合并的最大放能率要大于S-S型黑洞合并的最大放能率.

若是2个Kerr黑洞合并（K-K型），质量和角动量分别为M1、M2和 J1、J2.同理采用面积定理及线性微扰展开并略去高阶小量可得K-K型黑洞合并的最大放能率为

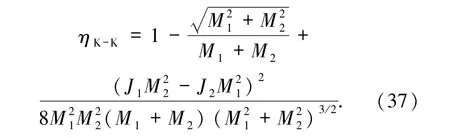
同样大于S-S型黑洞合并的最大放能率.

可见，由于角动量的存在，黑洞合并的最大放能率也会增大.可以定性地理解为黑洞具有角动量，使得能量因离心作用而更容易损失，因此放能率也相应增大.

下面考虑电荷对放能率的影响.若是2个Reissner-Nordstrom黑洞合并（RN-RN型），质量分别为 M1、M2，带电荷分别为 Q1、Q2.同理采用面积定理及线性微扰展开并略去高阶小量可得RN-RN型黑洞合并的最大放能率为

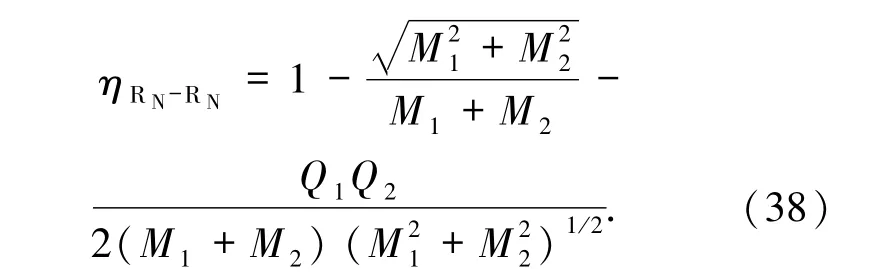
小于S-S型黑洞合并的最大放能率ηS-S（若Q1、Q2为同种电荷），大于S-S型黑洞合并的最大放能率 ηS-S（若 Q1、Q2为异种电荷）.可见如果原子黑洞均带同种电荷则会减小合并后的放能率，但两子黑洞若是带异种电荷则合并后会相互抵消，因此对放能率的影响也相应减弱.同样我们注意到，采用线性微扰展开后，电荷对放能率的影响依然表现为两个电量的乘积项（与面积增量的情况一致），也就意味着如果只有一方带电，那么这一项为零，即单方带电亦对放能率没有影响.由此也可推论，SRN型黑洞合并的最大放能率应与S-S型一致，K-KN型黑洞合并的最大放能率应与K-K型相同.实际经过具体计算也可得出这样的结论.

对于Reissner-Nordstrom黑洞与Kerr-Newman黑洞合并（RN-KN型），质量分别为 M1、M2，带电荷分别为Q1、Q2，Kerr-Newman黑洞角动量为J2.同理可计算得RN-KN型黑洞合并的最大放能率为

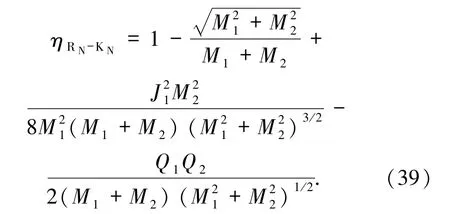
比 ηS-K小（若 Q1、Q2为同种电荷），比 ηS-K大（若Q1、Q2为异种电荷）.与S-S型黑洞合并的面积增量 δAS-S比较，若

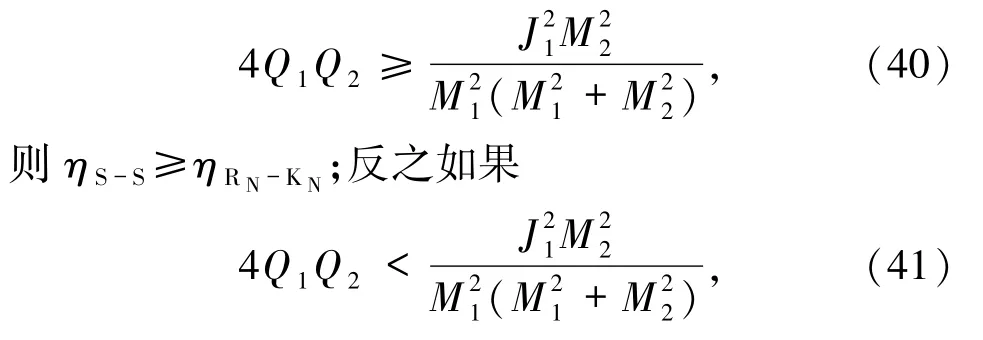
则ηS-S＜ηRN-KN.

对于2个Kerr-Newman黑洞合并（KN-KN型），质量分别为 M1、M2，带电荷分别为 Q1、Q2，角动量分别为J1、J2.同理可计算得RN-KN型黑洞合并的最大放能率为

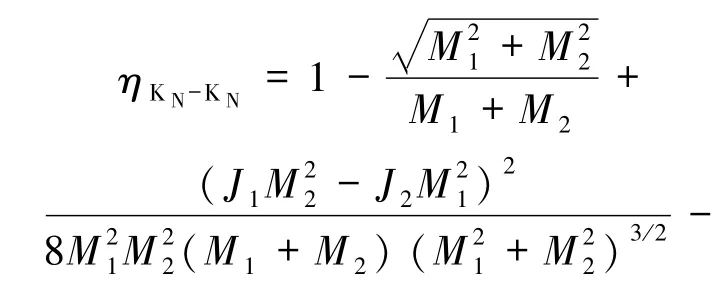
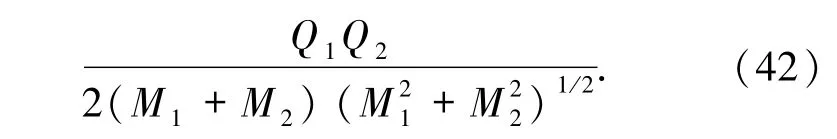
比 ηK-K小（若 Q1、Q2为同种电荷），比 ηK-K大（若Q1、Q2为异种电荷）.与S-S型黑洞合并的最大放能率 ηS-S比较，若

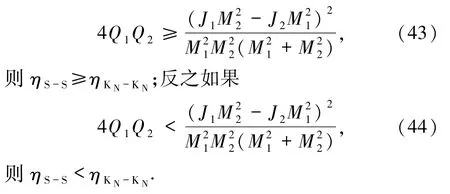
综上所述，对于双黑洞合并后的最大放能率大小比较，顺序依然与面积增量的情况相同，即：

1）若 Q1、Q2为同种电荷，有

另一方面，最大放能率亦不能超过1，得到RN-KN型及KN-KN型黑洞合并原子黑洞带电的临界条件分别为：

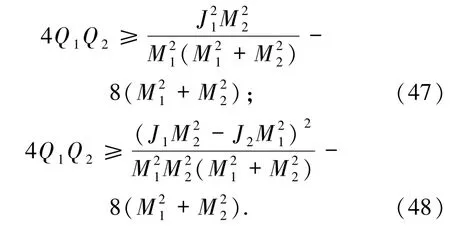
带同种或异种电荷均应满足这一条件.

3 结论与讨论

本文在广义相对论中研究了几种类型黑洞相互合并后的面积增量及放能率，结果表明角动量虽然会使黑洞自身的表面积减小，然而却会增大黑洞合并后的面积增量.Bekenstein［10］指出黑洞面积即等价于黑洞熵，因此，如果原子黑洞存在角动量，则合并后的黑洞熵的增量将增大，黑洞将变得更加无序.如果原子黑洞带电，带异种电荷合并后的面积增量也将增大，从而黑洞熵增量亦增大，黑洞也将变得更加无序；然而若是带同种电荷反而会使合并后的面积增量减小，也即意味着合并后黑洞的熵增量减小，可见带同种电荷会降低合并后黑洞的无序性；但如果只有一方带电，则对面积增量没有影响.对于放能率方面，角动量与电荷对其的影响与面积增量的情况实际上相同—由于角动量的存在会使最大放能率增大，这可能是因离心作用使得能量更容易脱离黑洞的束缚而被释放的缘故.若存在电荷，假如带的是异种电荷，则合并过程的最大放能率也会增大；但是如果带的是同种电荷，则最大放能率反而会减小；若只有一方带电，则对放能率也没有影响.

另外，既然黑洞外视界面积可看作黑洞熵，则在合并过程面积增量即应大于零.因同种电荷会减小面积增量，由此可知对RN-KN型及KN-KN型黑洞合并原子黑洞带电应该有个极限条件，分别为文中（28）和（29）两式.如果超过此临界条件，面积增量将为负值，即意味着合并过程熵为负.根据黑洞热力学第二定律，这一过程是不可能进行的；然而反过来，由此大黑洞分裂为两带同种电荷的子黑洞理论上是可行的.下面来讨论这一极限条件能否达到.考虑R-N黑洞的情况应有Q1Q2≥2M1M2，写成国际单位制为Q1Q2≥2GM1M2，即

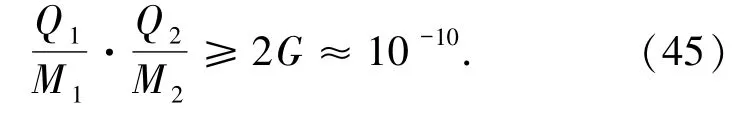
即只要2个子黑洞的荷质比数值大于10-5即可.我们知道慢速电子的荷质比约为1011量级，质子的荷质比约为107量级.一般原子核的中子数与质子数相近，荷质比也约为107量级.因此哪怕是原子序数较大的原子仅失掉最外层一个电子，其荷质比也不会低于105.退一步讲，即使1010个这样的原子只有一个失掉一个电子，总荷质比就可达到10-5，显然这是很容易达到的.然而黑洞荷质比达到这一量级对于R-N黑洞将会出现一问题——此时已超过极端黑洞条件，内外视界将重合并消失.但是只要取适当的值（其中一个黑洞荷质比取小点，另一个取大点），则大黑洞及其中一个荷质比小的黑洞均不会超过极端条件，然而不可避免另一个黑洞已经达到“super-extremal”条件［18］.之前由面积定理得出的一个重要推论就是一个黑洞不能分裂为2个，这是正确的.然而当一个黑洞趋于极端条件时，时空几何分裂为一个极端黑洞外加一个（根据Carroll等的工作）不连续的紧致的AdS空间，其熵没有消失，而是转移到了额外的自由维度（弦理论或M理论预言的其余紧致的6维或7维空间）［19-22］.可见一个大的黑洞时空几何“分裂”后，至少应有一个为弦理论所预言的紧致空间.当黑洞接近极端条件时，虽然熵在我们所处的四维时空减小并趋于零，但并没有消失，因此热力学第二定律依然成立.

希望通过本文的研究能对天文上观测鉴别不同类型的黑洞以及验证不同类型的引力理论提供一定的理论依据和新的研究途径.