关联成像及其应用研究进展

蔡阳健

（1.山东师范大学物理与电子科学学院，山东济南250358； 2.苏州大学物理科学与技术学院，江苏苏州215006）

1 关联成像简介

1.1 引言 通过对光场强度涨落进行关联运算所获得的成像，被称之为“关联成像”（有些学者称其为“关联光学”、“符合成像”或“量子成像”）［1］.关联函数作为像的载体，其自变量的空间位置有2种取值方式：第一种，2个自变量均取在包含物体的光路中，如文献［2］；第二种，一个自变量在包含物体的光路中取值，而另一自变量则在不包含物体的光路中取值，如文献［3-14］等.前者类似于20世纪50年代中期，美国科学家Hanbury Brown和Twiss利用光场强度涨落的关联函数来测量星体角尺寸的研究成果［15］，称HBT型关联成像.后者由于物体的像（包括几何像以及能呈现傅里叶变换的衍射像）可呈现在并不包含物体的光路上，而被称作“非局域关联成像”，或俗称“鬼成像”；其渊源可追朔到一个是20世纪初爱因斯坦-波多尔斯基-罗森佯谬（EPR佯谬）引发的“纠缠光子对”非局域性的研究.近年的研究表明，经典热光场也同样能实现这一成像而无需纠缠光源（如文献［6，10-11，13，16］等的报道）.2004年以来，国际上有关热光场关联成像的研究内容大多为鬼成像，而且它们多基于这种成像方式的特点和相对于普通成像的优点.这些特点和优点包括成像的“鬼”性质、在非相干光照明下可获得原本只能在相干光照明下才能获得的衍射图样（含傅里叶变换成像）［2-3，11-12］、可获得无透镜的几何成像和傅里叶变换成像（如文献［13，17］等）、仅需菲涅尔衍射距离即可实现无透镜的傅里叶变换［3，12］、以信息传输中的不利因素“噪音”为传输载体，化“不利因素”为“必要条件”、单像素成像［18-21］、获取衍射场的相位信息［22-24］、具有超越经典衍射极限的成像分辨率［2-3，14］，以及抵御大气折射率变化的扰动，成为大气光学研究的一个新方向等.

可见此成像方式的优势远不止是异于常识的“鬼特性”，而是其广阔的基础研究和应用基础研究的前景，譬如纳米和生物科技领域的显微成像［25］、高能物理领域的原子核探测［26］、量子光刻—突破经典衍射极限［14］，以及在大气光学领域的应用及其相关科学问题等.国际上该领域活跃着的知名学者如 Boyd、史砚华、Lugiato、Jonathan Dowling、赵复生等已于2005年在“综合性大学研究计划”（简称MURI）的支持下，形成以Boyd为负责人的国际研究团队，从事相关内容的研究.

在本文1.2～1.8小节中，将分别介绍鬼成像在光学相干和偏振领域、单像素成像、物体的复值获取、超越经典成像分辨率、X射线衍射成像、激光雷达领域的应用，以及其带给这些领域的突破和进展.在第2章中将对关联成像在大气湍流领域的研究做详细介绍.

1.2 历史起源和争论 1994年，俄罗斯科学家Klyshko等［27］在一篇讨论双光子光学的研究论文中预言，当包含纠缠光子的两束光之一经历如图1［27］所示的光路中的阻挡屏4时，其与另一束未经历阻挡屏光场的符合计数函数将以第二束光的空间坐标为自变量，呈现阻挡屏的边缘衍射条纹.这是鬼成像的最早报道之一.随后巴西 Ribeiro等［4］通过参量下转换的动量纠缠光源，以“符合计数”的方式观测到第一例“双光子干涉条纹”.1995年，Shi小组［5］也通过参量下转换获得的动量纠缠光源，观察到“鬼干涉”和衍射.在以上2个实验中，参量下转换产生的动量纠缠的“信号光”和“参考光”被偏振分束棱镜分成2个不同的“光臂”，而物体（杨氏双缝）放置在其中的一个光臂上.实验表明，含有物体的光臂并没有出现一阶干涉条纹；但当把“参考光”臂上的各点光场与参考臂上的某一固定点光场进行“符合计数”运算时，符合计数函数将呈现干涉条纹.由于该干涉条纹是以不包含物体的光臂空间坐标为函数的，所以所得的干涉条纹称为“鬼干涉”条纹.实现上述“鬼干涉”后不久，Shi小组［28］采用同一性质的光源，实现了位置空间的“鬼成像”，实验结果展示了一幅以“参考光”光束的光子为坐标的一组字母组合的清晰几何像；2004年，Boston小组［29］首先实现纠缠光源的纯位相物体的鬼干涉，得到了纯位相物体的菲涅尔衍射条纹；同年，Shi小组［30］利用这种成像方式来判定纠缠光子对的纠缠度.

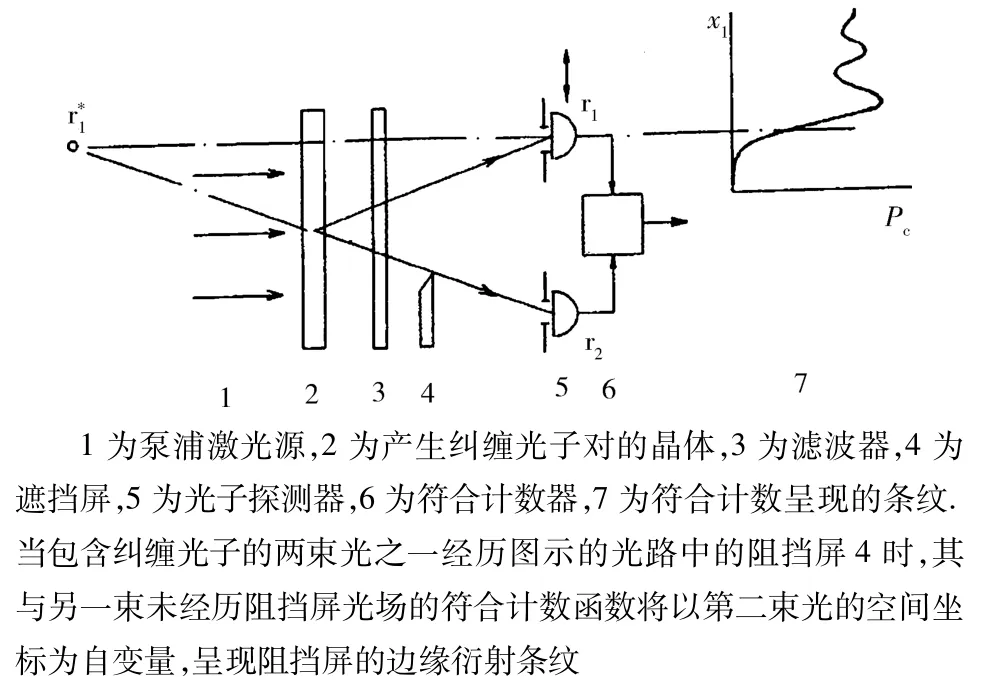
图1 关于鬼成像的预言Fig.1 The prediction for ghost imaging

文献［28］中指出“可能有某种经典热光源能够部分的仿效这种（非局域成像）行为”，但一直未能从实验上得以证实.因此，在相当一段时间内，“纠缠光源”是否是成像的必要条件一直存在着争论.Boston小组认为，纠缠光源是鬼成像的必要条件，尤其是在“鬼干涉”的情形下，纠缠光子对更是必要条件：“鬼成像的架构的确需要纠缠光源，经典热光源即使存在着关联，但如果没有纠缠，也不能实现鬼成像［31-32］”.做出此论断后不久，Rochester大学的Boyd小组即采用做小角度摆动的转镜模拟“热光源”，得到了鬼成像［16］.Cai等［6］通过解析计算得出，他们所产生的并不是“热光源”的鬼成像，而仅仅是物体的投影.此后Cai等［7］还在理论上计算了“热光源”鬼成像，分析了光源相干度对此时成像的分辨率和成像质量的影响，并指出了纠缠光源与“热光源”鬼成像之间的具体差异，该理论工作随后被Shi小组［8］通过实验进行了验证.这样一系列的报道引发了此后关于鬼成像在哪些方面需要光源的纠缠特性，哪些方面不需要光源的纠缠特性的讨论.意大利的Lugiato小组［33］在论文中指出：“经典热光源可以实现鬼干涉成像和几何成像；但如果要像 Shi小组［5，28］那样，仅通过调整参考臂的光路就能分别实现衍射成像和几何成像，只有纠缠光源才能实现”.很快，此论断再次被Rochester大学的Boyd小组用实验推翻［34］：当采用赝热光场照明时，仅仅通过调节参考臂上透镜的排布，即可分别实现几何成像与衍射成像，而光源和含有物体的光臂并未做任何改动.

图2 非局域成像的光路结构Fig.2 The optical setup for non-local imaging

文献［33］结论的得出，是基于这样一个理论：只有纠缠光源，才能在近场和远场（位置空间和动量空间）同时具有关联，而热光场在远场（动量空间）并无关联［35］.Boyd 小组论文［34］发表后不久，Lugiato 小组即发表论文［36］，肯定文献［34］的工作，并从量子光学的观点出发为Boyd小组的实验给出了理论根据，得到结论：当采用热光源时，图2［36］的 x1和 x2处热光场强度起伏的二阶关联函数可表示为

可见无论使用经典热光源，还是使用纠缠光源，参考光和信号光光路的点扩散函数，都将包含在（1）和（2）式中，据此不难推断，一旦参考光光路的点扩散函数h2（x，x2）为已知，那么关联函数将能够以休闲光光路中平面x2处的位置参数为坐标，再现物体信息—因为物体信息包含在 h1（x，x1）中.几乎与此同时，Han小组［11］从统计光学的角度出发，也得到了形如（1）式的结论，并指出，当适当选择2个探测平面x1和x2在光路中的位置时，关联函数将重现物函数的准确傅里叶变换，并展望了这种成像方式在硬X射线等缺乏相干源的场合的应用.此后，一般认为，“纠缠光源”、“纠缠光子对”不是鬼成像的必要条件.不仅如此，Boston研究小组［37］还于2005年从Wolf方程

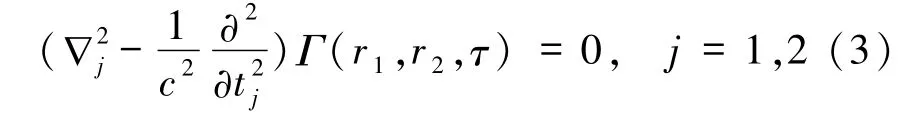
的角度，给出了基于“纠缠光源”和“经典光源”鬼成像以及量子光刻的统一解释.

需要说明的是，关联成像（符合计数、强度关联）的本质究竟是经典的统计效应还是“量子效应”，仍有争议.一方面，以 Shi小组［38］为代表的观点认为，量子成像的本质是量子的，即只有量子理论才能解释这一现象；另一方面，以Lugiatto、Bassano小组［39-41］为代表的观点认为，经典统计光学仍能解释Shi小组用以反驳经典观念的实验现象，因此不能把这一现象看作单纯的量子效应.

1.3 相干性和偏振性对鬼成像的影响 光场的相干性对成像，尤其是衍射成像起着至关重要的作用.单就经典的衍射条纹的获取而言，光场的相干性是积极因素，即光场的相干性越好，获取衍射条纹的对比度和分辨率越高.相干性对于衍射场的影响已有很成熟的研究，文献［42］是Wolf于2013年就相同的正弦光栅，分不同的相干性给出的不同的衍射条纹，可以很容易看出光场的空间相干性对衍射条纹的影响，见图 3［42］.

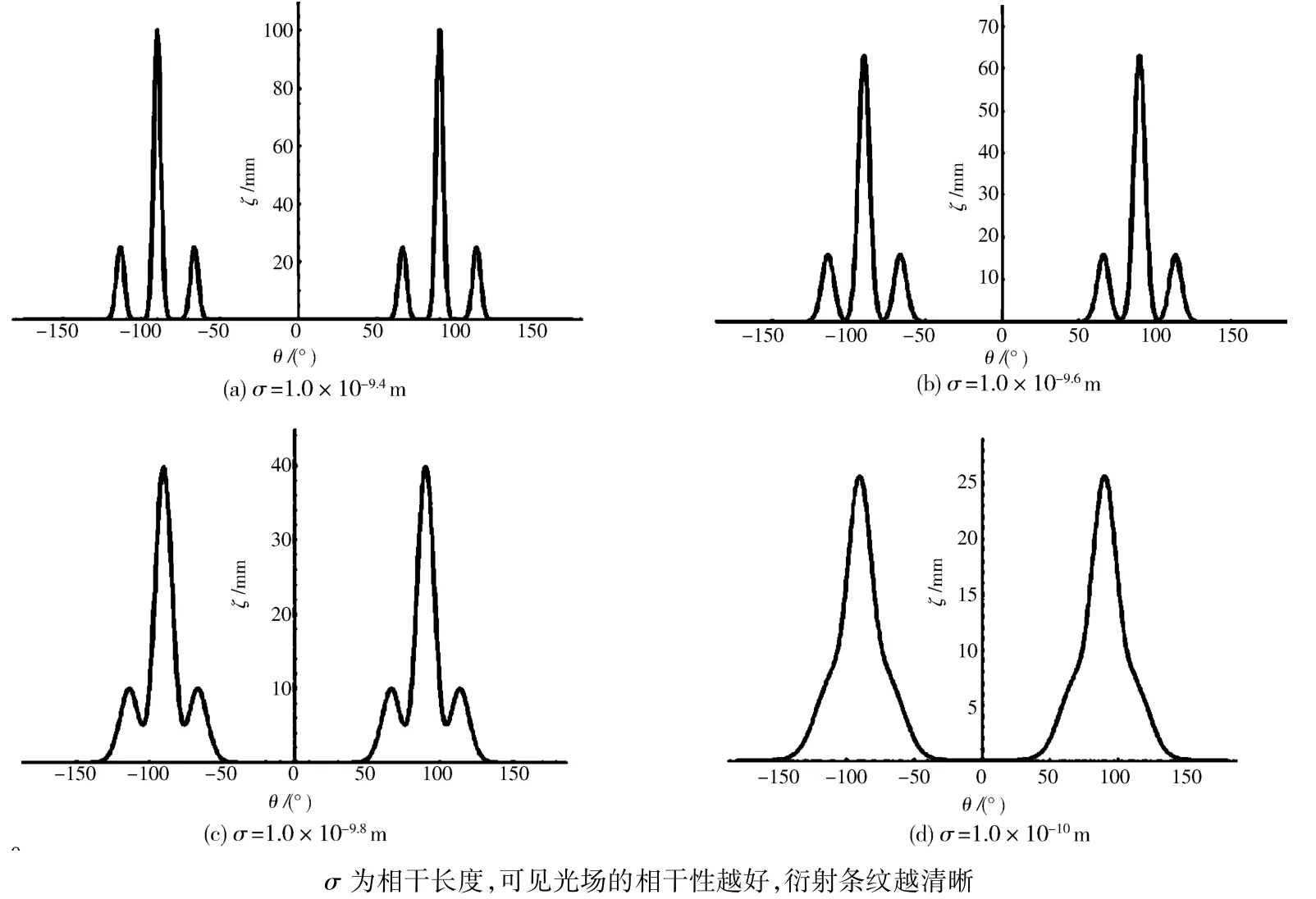
图3 同一正弦光栅在不同空间相干性的单色光场照射下的衍射条纹Fig.3 Diffraction pattern of a Sinusoidal grating under the illumination of monochromatic light with different values of spatial coherence length

光场相干性对于鬼成像的影响与经典成像不同，也是鬼成像研究的核心问题之一.Cai等［6］在2004年的研究明确指出了光场相干性对于经典成像和鬼成像所表现出的显著差异：光场的相干性越高，条纹的对比度和分辨率越低，见图4［6］.这表明鬼衍射和经典衍射对于相同的相干条件的光源，有着近乎相反的成像表现.此外相干性与鬼成像质量的关系也有报道［7］，图 5［7］（a）～ （c）所示为相同条件下，相干长度依次为 0.001、0.005、0.01 mm 的杨氏双缝的鬼成像图形.可以看出较低的相干性能够获取更高质量的鬼成像.

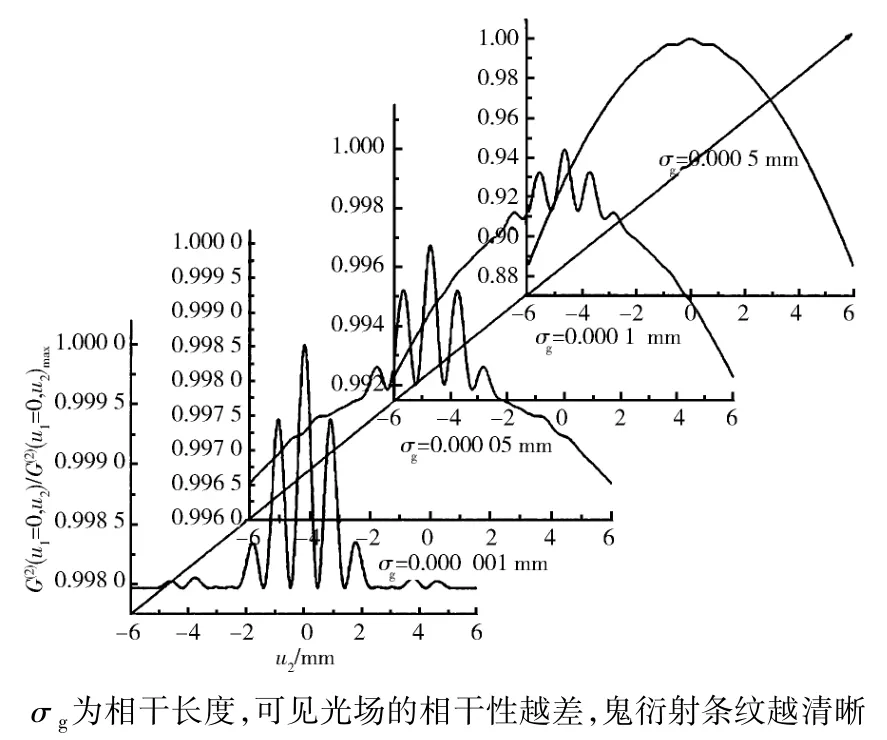
图4 同一杨氏双缝在不同空间相干性的单色光场照射下的鬼衍射条纹Fig.4 Ghost diffraction pattern of Young’s double-slit under the illumination of monochromatic light with different values of spatial coherence length

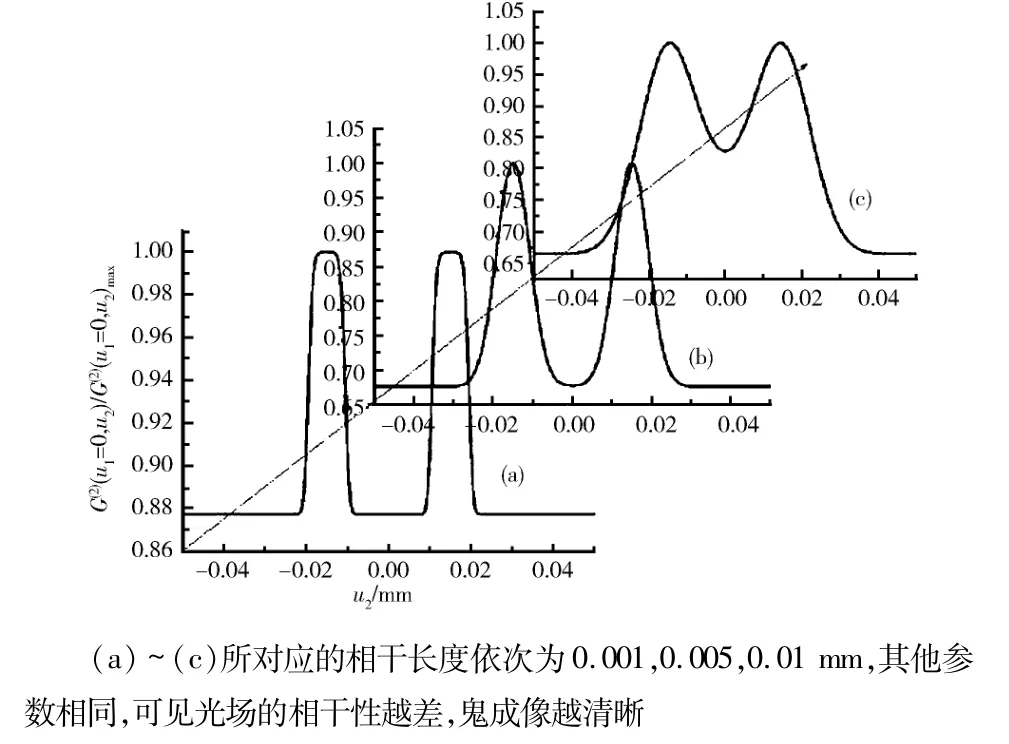
图5 同一杨氏双缝被不同空间相干性的单色光场照射下的鬼成像Fig.5 Ghost image of Young’s double-slit under the illumination of monochromatic light with different values of spatial coherence length

2011年，Friberg等［43］研究了照明光场偏振度P与鬼成像能见度的关系，他们得到的是一个普适的结论，既不针对特定的成像物体，也不针对具体的鬼成像架构，表达非常的简洁，即

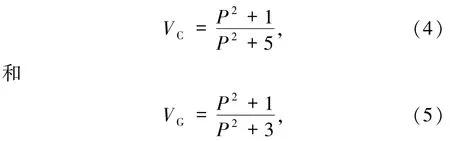
其中，VC和 VG分别为 Cao 等［45］和 Gatti等［46-48］在各自工作中定义的鬼成像能见度，它们分别为：

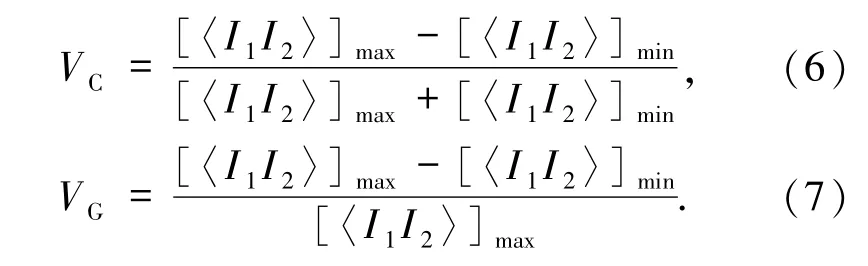
根据（4）和（5）式，照明光束的偏振程度决定成像能见度的情况，从完全非相干到完全相干，可一目了然地呈现于图 6［45］.

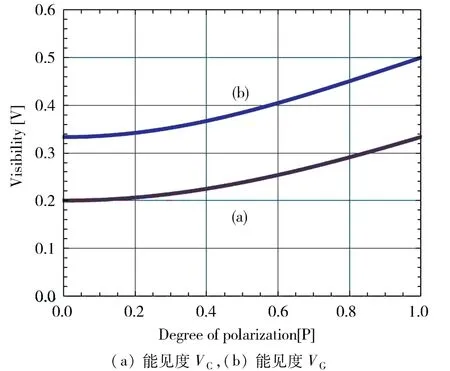
图6 鬼成像的能见度与照明光场偏振度的关系Fig.6 Dependence of the visibility of the ghost image on the degree of polarization of the incident beam

此外，Cai等［4］关于电磁光束鬼成像的论文在实验上详细地讨论了上述文献［43］的关于鬼成像能见度的表达式，并用实验验证了以上定义的恰当性.

有一类光束的相干性不具有空间不变性，也就是说其相干度不能单纯以空间坐标差为自变量.典型代表是相位扭曲高斯谢尔模光束，其谱相干度

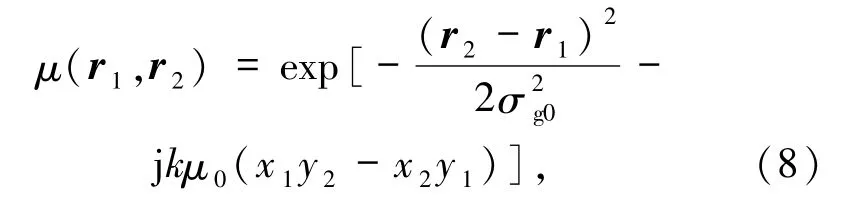
其中，ri＝ （xi，yi）为位置坐标，μ0为衡量相干程度之外的相位扭曲度，它对部分相干光场的传播也起着重要的作用.2009年，Cai等［49］研究了相位扭曲度对鬼成像的影响.以图7［49］所示的待成像物体为例，光场相位扭曲度μ0由小到大的鬼成像情况如图8［49］所示，可见扭曲度越大，成像的失真也越大.

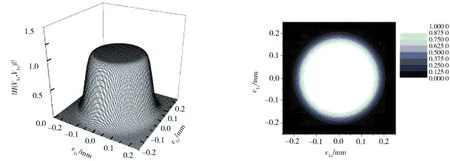
图7 待成像物体—圆孔，用于研究相位扭曲度对成像的影响Fig.7 Circular aperture for investigating the effect of twist factor on the ghost image

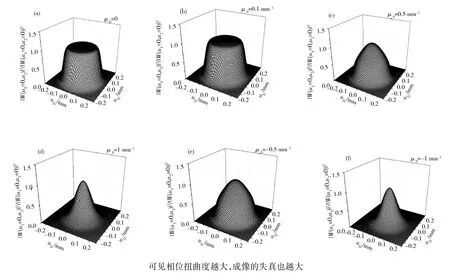
图8 具有不同相位扭曲度的照明光场所对应的鬼成像Fig.8 Ghost image under the illumination of light with different values of twist factor

1.4 基于鬼成像原理的“单像素”相机 近年来“单像素相机”［18］引起了广泛的关注，其基本思想为：参考臂的光场由事先预置的散斑场取代随机散斑场，并由该事先预置的散斑场照明待成像目标.这样，参与关联运算的两路信号中，只需由点探测器或无空间分辨率的桶状探测器获取物臂这一路的信号（见图 9［18］（b）），而不再需要测量依靠有空间分辨率的探测器获取参考光信号（见图 9［18］（a））.有些学者认为这种成像［50］中参与关联运算的参考光束为计算机模拟而并非真实的光束，因此同时被称为“计算鬼成像”［50-51］.

应用这一思想的第一次实验见于2009年，Bromberg的报道［18］，所用的成像目标为一平面物体.2013年，英国学者Padgett［20］应用这一思想在期刊《Science》上首次报道了三维物体单像素成像.在他们的报道中，预设的散斑场经由空间光调制器SLM照射待成像物体（图 9［18］（a）和图 10［20］），物体的透（图 9［18］）反（图 10［20］）射光场，经由桶状（点）探测器接收并记录，然后与先前预置的散斑场进行关联计算，得到物体的像.在Padgett的报道中，4个不同的视角的成像分别由4个不同位置点探测器（图10［20］）测得的光场强度时间序列与预置散斑场的时间序列进行关联运算而获得.图11［20］是文献［20］所报道的成像结果，图中行标i是参与运算的独立散斑场数量，列标 left、right、top、bottom 分别为左、右、上、下4个视角.

1.5 复物体的获取 通常所说的成像，系指振幅型物体（如杨氏双缝、电影胶片、景物等）的光场强度函数在空间的重现.而相位型物体（如透镜、折射棱镜以及动物上皮组织细胞等）由于对光场的强度几乎无调制作用，其相位信息则往往通过修改频谱的手段，线性的转化为强度信息（如相衬显微镜）.但是，相衬法对于相位起伏大于1弧度的物体并不能准确测出其相位，此时可通过其弗朗禾费衍射条纹推算其相位透射函数.遗憾的是往往有这种情况：物体远比单一的“振幅型”和“相位型”复杂，这类物体（如吞噬了碳纳米管的上皮组织细胞）同时具有振幅信息和相位信息，其物函数为复变函数，被称为“复物体”.采用传统成像的手段完整获取复物体物函数的手段，远比单一的振幅型或相位型物体困难.但鬼成像可以解决这个问题.

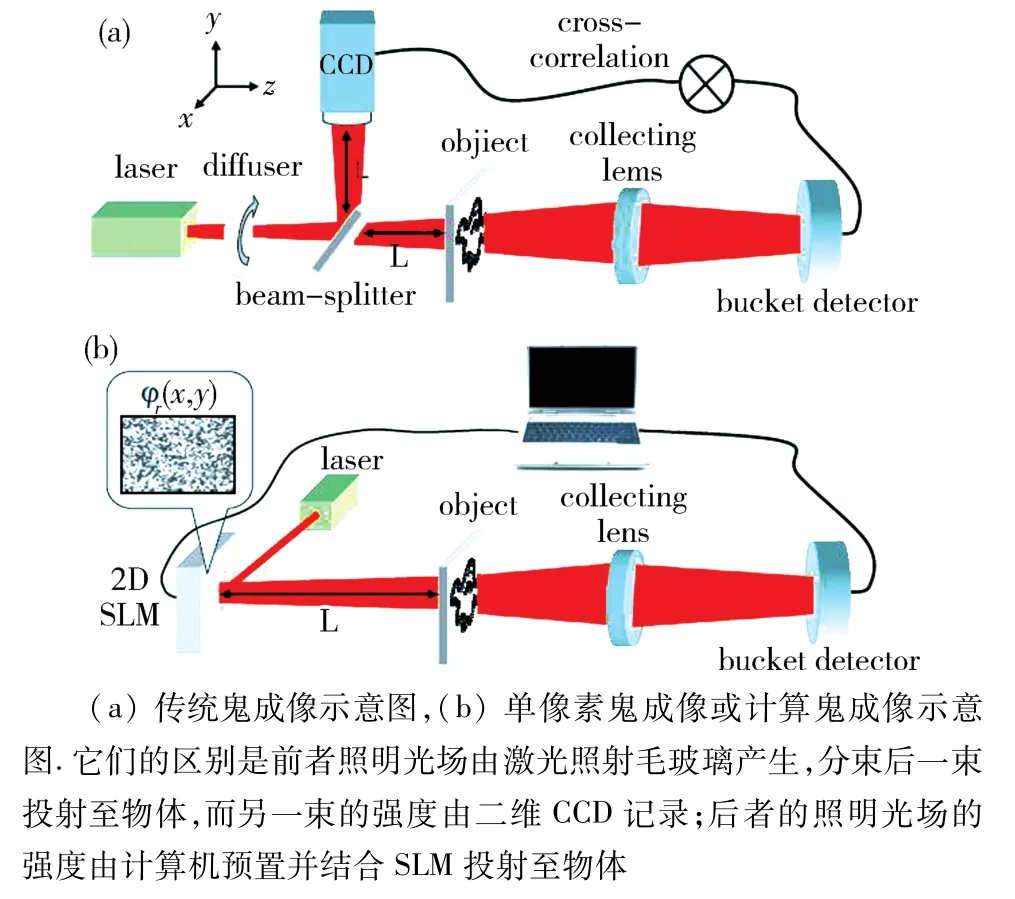
图9 传统鬼成像示意图及单像素鬼成像或计算鬼成像示意图Fig.9 The setup for classical imaging and the set up for single pixel computational ghost imaging

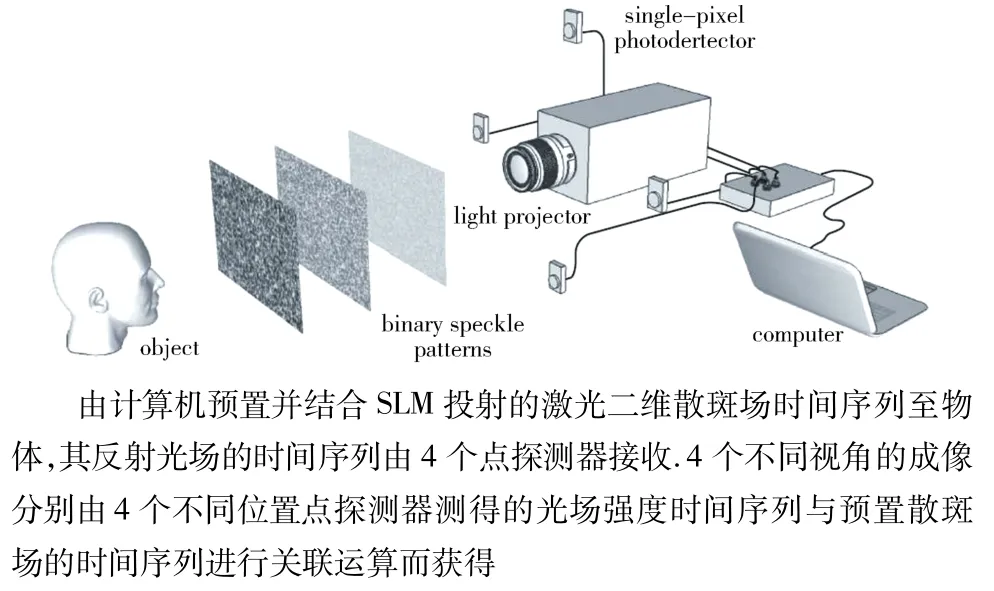
图10 第一例单像素3D成像原理示意图Fig.10 The setup for the first 3D single pixel imaging

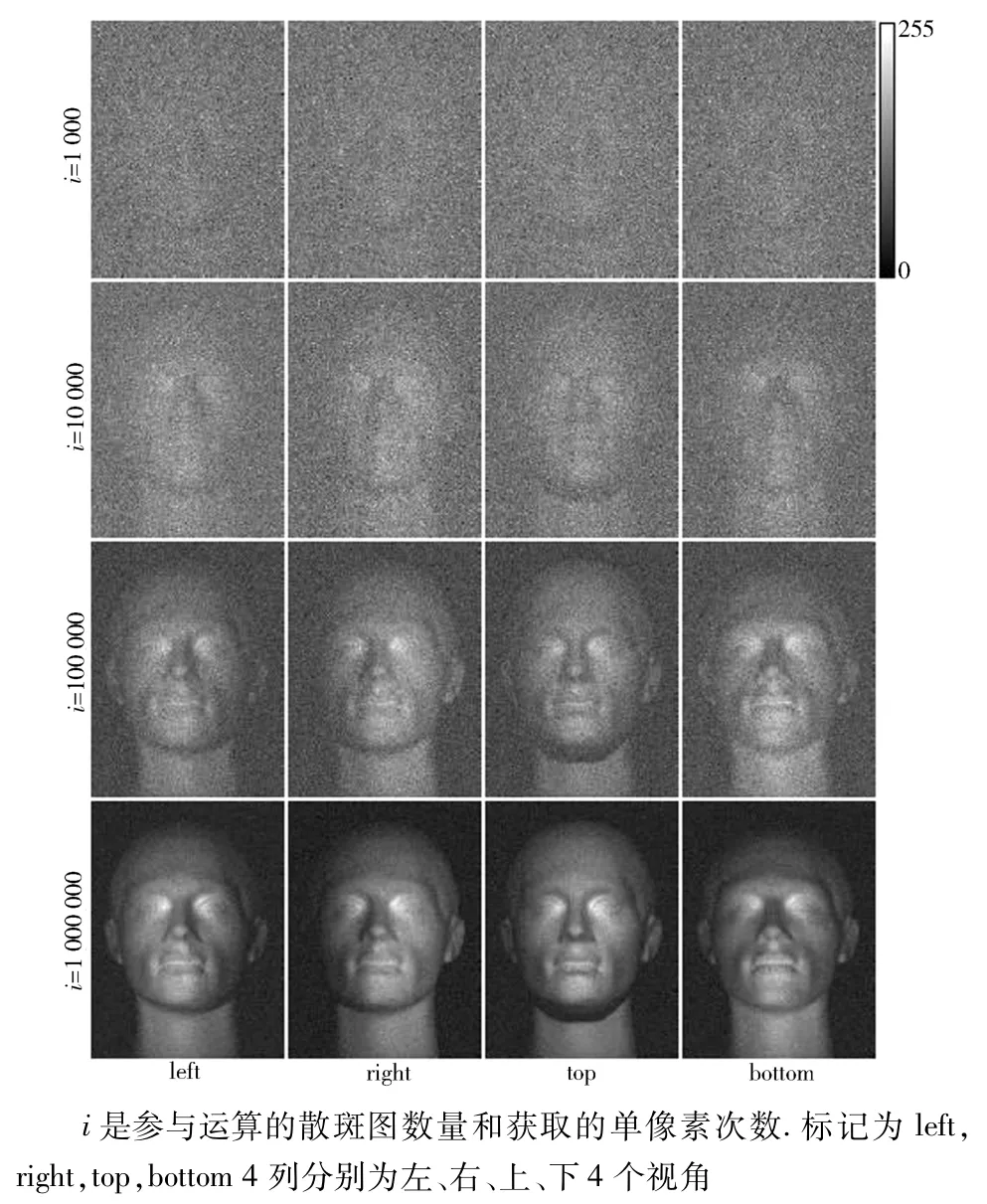
图11 第一例单像素3D成像图Fig.11 The setup for the first 3D single pixel imaging

最早用鬼成像手段获取复物体信息见于Gori等［22］学者的报道（图 12［22］）.在图 12［22］所示的光路中，由旋转毛玻璃产生的赝热光源经分束棱镜分为两束，其中之一照射复物体S，其中之二则不经过物体.上述两束光场通过望远镜系统M于平面Π3重叠，干涉场的复信息由杨氏双孔（图12［22］中的Y）和由透镜L2和O2构成的望远镜系统观察.所观察到的干涉条纹的振幅可计算出Π3平面干涉场相应点的振幅（图13［22］），条纹的初相位 φ 代表 Π3平面干涉场的相位φ.该方法的核心为鬼衍射两臂的关联函数为复物体函数的傅里叶变换，即

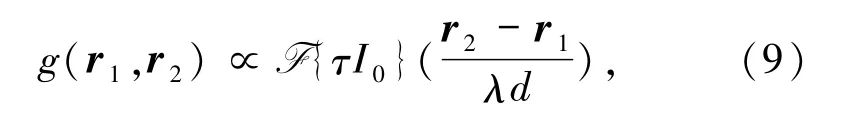
其中，τ是复透射率，I0是光场的强度，λ是光波波长.而在杨氏双孔Y的干涉条纹强度分布

中，可计算出（9）式g的振幅｜g｜以及直接读出g的相位φ.最后将所得的复函数g（r，-r）进行反傅里叶变换，即可得到物体的复函数.关于复函数g自变量取值为何为对称坐标（r，-r）的原因可见关于“波前反向杨氏干涉仪”的文献［23］.

2007，Han小组［3］对鬼衍射和HTB实验进行了对比，表明HBT实验获取的衍射条纹为物体复透射率的模平方的傅里叶变换，而鬼衍射实验获取的是物体复透射率的傅里叶变换.基于对由前、后者实验综合而成的“两步法”，他们获得了复物体的复透射率［24］.2010 年，Han 小组［24］在鬼成像架构中加入马赫曾德干涉仪，也给出了获取复物体信息的数值模拟结果.同年Zhang等［52］提出使用热光场结合相位板分2次分别获得复物体实部和虚部的相位信息.

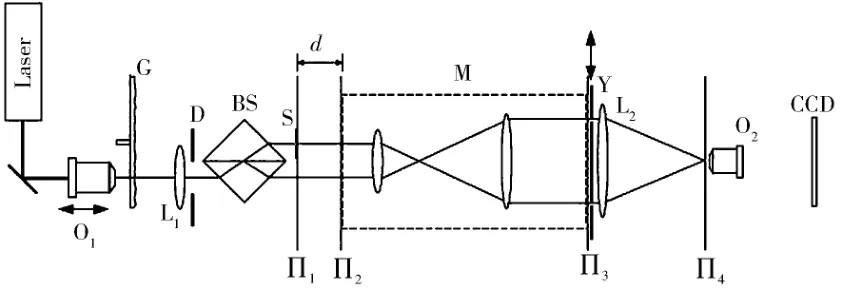
图12 Gori等学者用于获取复物体信息的鬼成像架构图Fig.12 The ghost imaging setup for complex object acquisition by Gori et al

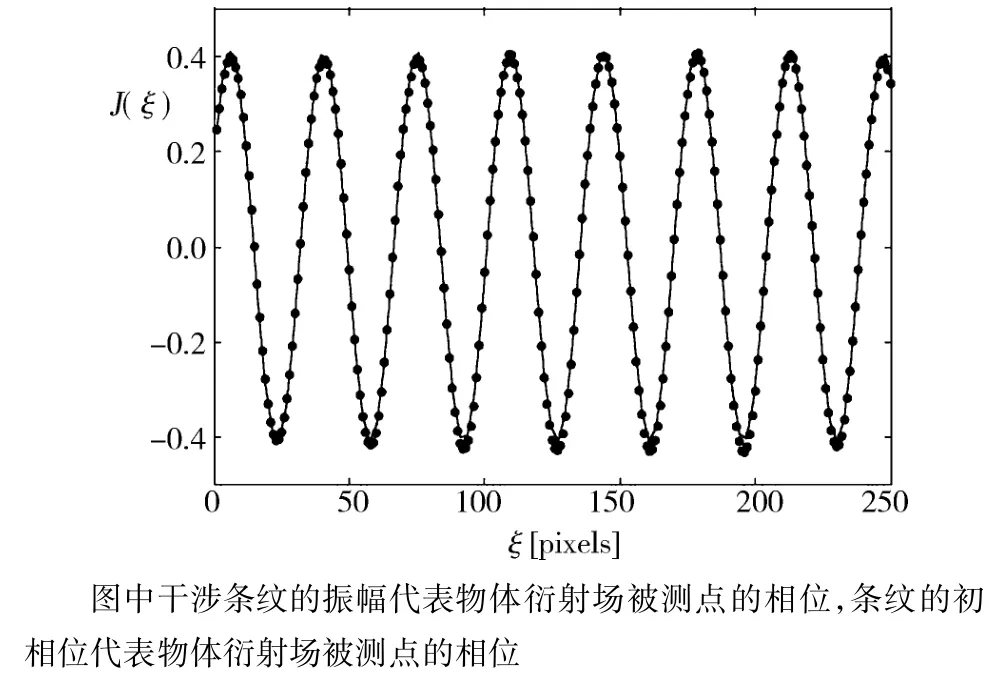
图13 Gori等学者用鬼成像架构获取的复物体信息Fig.13 Information of a complex object obtained through ghost imaging by Gori et al

1.6 超越经典成像分辨率 由于衍射的原因，光学成像系统的角分辨极限为

此为“瑞利判据”，规定了在经典的光学系统中，对于角距离小于Δθm的2个点是无法分辨的.突破此极限，一直是学界的追求.作为这方面工作的杰出代表，Betzig等［53］3位科学家因扫描荧光显微技术而获2016年度的诺贝尔化学奖.

鬼成像可以作为突破经典分辨率的重要手段，其中量子光刻是重要内容.

文献［11］表明，用非局域关联成像的方法获得亚波长干涉条纹的主要过程是在两臂选取相对于分束棱镜“反对称”的点进行关联运算.在这种运算方式的启发下，文献［54］设计出如图14［54］的光路构造，使得两臂“反对称”像素（x1＝-x2）点能通过光路“折叠”到同一个点P上.图14［54］的感光介质采用“双光子吸收介质（TPA）”，只对光场的“二阶效应”，即光子的“符合计数率”感光，而对通常意义下的“一阶效应”不感光.结合以上的分析可知，采用图14［54］反映的实验架构，物体的傅里叶变换成像，将以2倍于经典衍射极限的分辨率呈现在TPA介质上.其物理本质在先前提及的双光子Wolf方程的研究中已有阐述［37］.2009 年，Han 小组［14］以杨氏双缝为成像物体，从实验上对比了经典成像和鬼成像在相同传输距离的前提下的分辨率对比情况，实验测量如图15［14］所示，实验表明鬼成像在同等条件下可以获取比经典成像更高分辨率的图像.

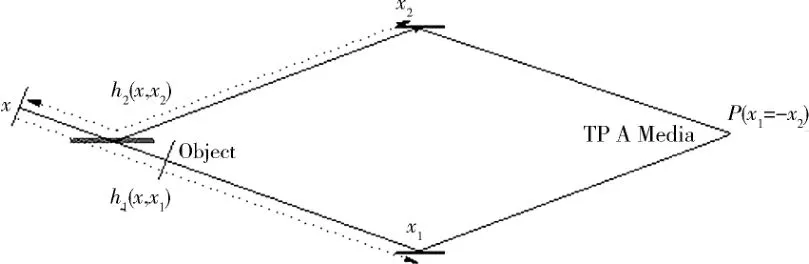
图14 两臂“对称”像素（x 1＝-x 2）点能通过光路“折叠”到同一个点P上Fig.14 The“symmetrical”pixels（x 1＝ -x 2）of the two arms can be folded to the same point P through the optical path

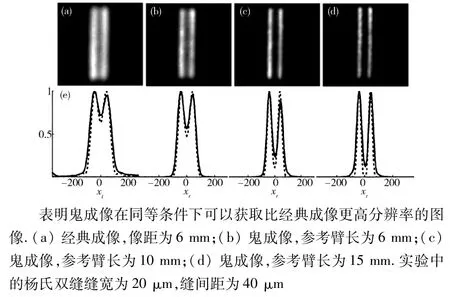
图15 文献［14］所给出的经典成像和鬼成像的对比实验结果Fig.15 Comparison results of classical imaging and ghost imaging given in ［14］

此外，由于以两臂对称像素（x＝x1＝-x2）位置为自变量的鬼衍射获取条纹的频域比相干衍射的频域宽一倍，因而同等视域下，所获得的空间频谱是相干衍射所获取频带宽度的2倍（即亚波长干涉、衍射条纹）.使用鬼衍射条纹经反傅里叶变换获得的图像，其分辨率也是经典成像分辨率的2倍［2-3］.

1.7 X射线衍射成像 1912年，德国科学家MTF von Laue成功地进行了胆矾晶体的X射线衍射；1913年，英国学者Bragg导出X射线反射的Bragg方程；1914年，Bragg父子率先测定出金刚石、氯化钠、氯化钾等晶体的结构.以此为标志，早在20世纪初就开始创建的X射线结晶衍射学.它们对科学技术的推动作用非常明显地表现在材料科学、生物构造学以及其他领域.目前的扫描探测技术仅能够探测被成像物体的表面结构；电子显微镜能为晶状材料提供原子级别分别率的图像，但探测厚度最大只能达到50 nm；对于大分子聚合物和无机材料，电子显微镜的分辨率将更低.所以，若要在纳米级范围内探测到高分辨率的分子内部三维结构，自然会考虑相干X射线衍射成像（CXDI）.尽管相干X射线衍射成像具有很大的应用潜力，但仍面临两大难题：一是高相干度的X射线激光（相干X光光源）目前仍不可能实现；二是结晶衍射成像要求被成像物必须有周期性的空间结构，而对于无机纳米材料和部分生物分子结构的物质，很难进行结晶.因此，对于这2个困难，人们尝试利用经典热光场的无透镜傅里叶变换成像手段来获得突破.

Han团队［11］曾于2004年提出这方面的理论构想，2007年使用赝热光源进行了原理验证［12］，并于2016年使用硬X射线实现鬼衍射，从鬼衍射条纹中恢复出样品的像函数［55］.在如图 16［55］（a）所示的装置中，硬X射线通过狭缝照射移动的金箔，使得金箔后方的X射线强度起伏形成赝热X光源.物臂信号和参考臂信号分2次获得.第一次，待成像物体放置于光路中，由CCD测得强度起伏信号ΔIt（xt），作为鬼成像的物臂信息；第二次，待成像物体并不放置于光路中，由CCD记录强度起伏信号ΔIr（xr）作为鬼成像的参考臂信号.图16［55］（b）下部为某一时刻ΔIt（xt）和 ΔIr（xr）的图样.图 17［55］中，（a）、（b）为两臂强度起伏“互关联”函数图样及其剖面图，此为物函数的傅里叶变换图样；（c）、（d）为物臂强度起伏的“自关联”函数及其剖面图，此为物函数模平方的傅里叶变换；（e）、（f）为硬 X射线直接照射的衍射图样及其剖面图.对照（e），可见（a）和（c）不仅条纹更加清晰，更重要的是，它们分别包含了振幅和位相的综合信息，以及振幅的单独信息，可以精确地利用反傅里叶变换变换进行图像的反演.

与上述硬 X射线实现鬼衍射同期，Pelliccia等［56］认为X射线成像过程中光场强度因样品的吸收而导致的衰减的同时，信噪比也会明显地下降.但对于鬼成像，则参考臂的强度不会被成像目标衰减，且关联程度也不会随强度而衰减.基于这个优点，他们报道了同步辐射部分相干X射线的鬼成像［56］，实验原理如图18［56］所示.分束镜将同步辐射部分相干X射线分为两束：其中一束照射待成像目标，另一束自由传播.两束光照射摄像机的同一感光面的不同区域，如图19［56］所示.与前述工作不同，两束光所形成动态散斑的动力来源一是同步辐射装置电子束的散弹噪音，具有关联性；另一个是分束镜的低频振动，没有相关性.在实验中，使用傅里叶滤波的方法把后者滤掉，而使用前者进行关联运算.在进行关联运算时，对物臂的强度记录进行了空间积分，使其等效于不具有空间分辨能力的桶状探测器信息.然后该信息在与参考臂的动态散斑场进行关联运算.以参考臂为坐标的关联函数呈现的待成像目标的投影即为所获得的鬼成像.

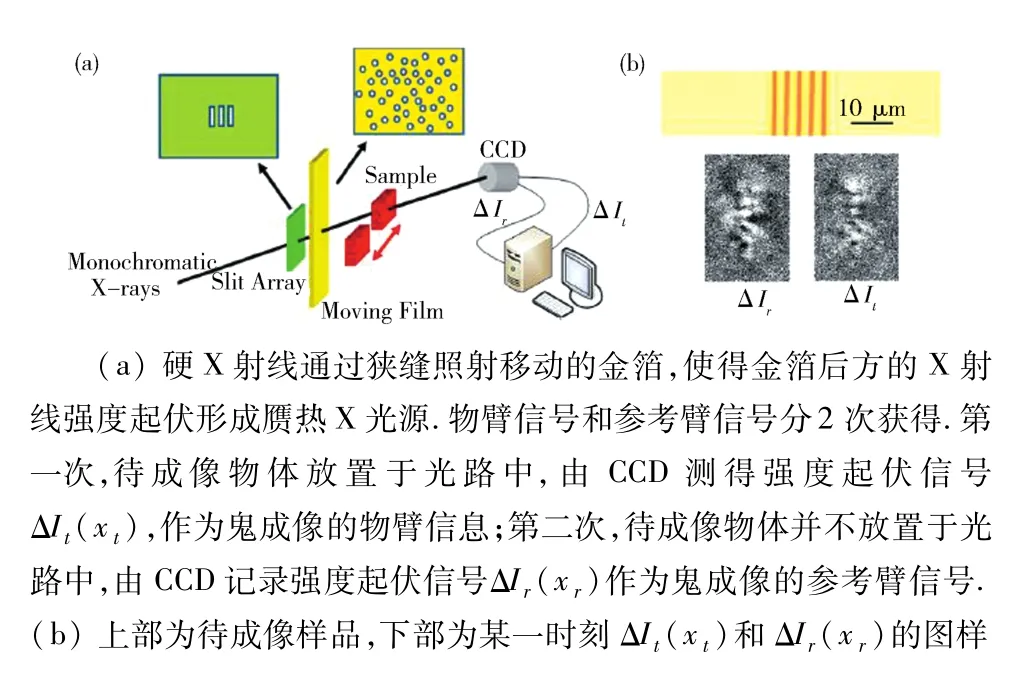
图16 硬X射线傅里叶变换鬼成像（鬼衍射）示意图Fig.16 The optical setup for Fourier transform ghost imaging with Hard X ray

考虑到高强度的X射线对待成像目标可能的伤害，2018 年，Wu 等［57］学者采用“计算鬼成像”的方式，用台式X光机发出的较小强度的X射线获得了物体的几何像.比传统X光投影成像具有更高的衬比度-噪声比.此外，以色列学者Shwartz等［59］也报道了较小强度的X光显微成像.

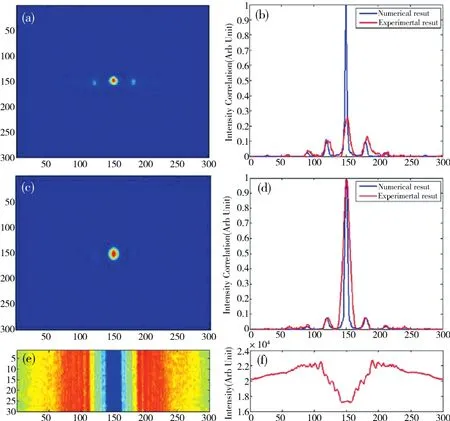
图17 （a）、（b）两臂强度起伏关联函数图样及其剖面图-物函数的傅里叶变换图样；（c）、（d）物臂强度起伏的自关联函数及其剖面图-物函数模平方的傅里叶变换；（e）、（f）硬X射线直接照射的衍射图样及其剖面图Fig.17 （a）、（b）Correlation function of two arms for the intensity fluctuations and its cross-section，the pattern was the squared modulus of the Fourier transform of an object；（c）、（d）Autocorrelation function of the object arm for the intensity fluctuations and its cross-section，the pattern was the squared modulus of the Fourier transform of an object’s modulus；（e）、（f）the diffraction pattern when the object was illuminated by hard X ray

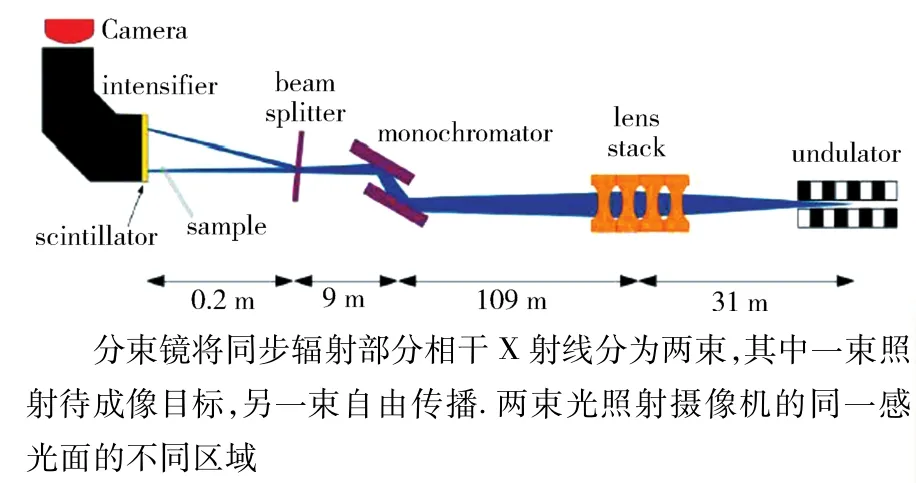
图18 部分相干同步辐射X射线鬼成像实验Fig.18 Ghost imaging experiment illuminated by partially coherent synchrotron X ray

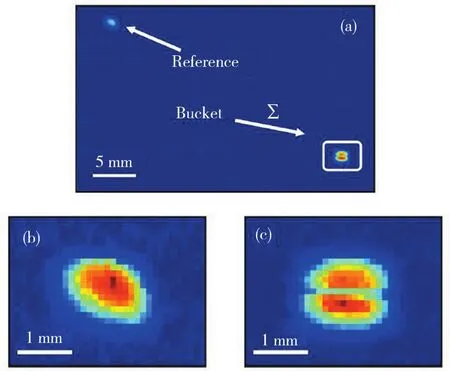
图19 两束光照射摄像机的同一感光面的不同区域Fig.19 The two beams illuminate different areas of the same photosensitive surface of the camera

1.8 激光雷达 鬼成像以关联函数为载体呈现待测物体的像，而参与关联运算数据为大量的、于不同相干时间内测得的数据.远距离鬼成像属于遥感成像领域的激光雷达.图 20［60］为韩申生等［59-60］于2012年同步辐射部分相干X射线分为两束：其中一束照射待成像目标，另一束自由传播.（a）同一高速摄像机同一感光平面不同位置拍摄的动态散斑，（b）参考臂信号具有空间分辨信息，（c）对物臂的强度记录进行了空间积分，使其等效于不具有空间分辨能力的桶状探测器信息实现遥感鬼成像的装置图.由脉冲式激光器和毛玻璃组成的脉冲式赝热光场［59］的光脉冲时间序列由分束棱镜分为两束：一束照射远程目标，远程目标的反射光场脉冲序列由望远镜搜集；另一束自由传播的脉冲序列由具有空间分辨能力的CCD阵列记录，两路信号由“压缩感知关联运算”［60］方法进行运算.图21（图片来源于 http：／／www.siom.ac.cn／jgsz／lzgxzdsys／yjxz／）（a）和（b）分别为远程目标及其放大图，（c）为成像结果.此时获得鬼成像为二维图像尚不具备纵深信息.

为获得三维鬼成像，Yu等［61］利用散斑场的纵向关联的特性，结合待成像目标不同纵向深度的平面到参考臂探测器具有特定的延迟时间这一特点，逐层对三维目标进行成像，图22［61］为该方法的原理图.物臂的延时桶状探测器（TBD）可分别选择来自三维目标第i个纵向层面相对应的延迟时间为ti的光脉冲序列，与参考臂的二维散斑场进行“压缩感知关联运算”进而获得三维目标第i个纵向层面的“层析”图像.采用该方法，Gong等［62］于 2016 年发表第一篇3D单像素鬼成像研究论文.图23［62］（a）为各纵向层面所对应的不同延时时刻的反射光场强度，1～6是各层面的记号；（b）是待成像物体；（c）是由各层面“层析”所堆叠而成的三维鬼成像；（d）是三维成像的二维视图；（e）～（f）是不同纵向层面的层析图.

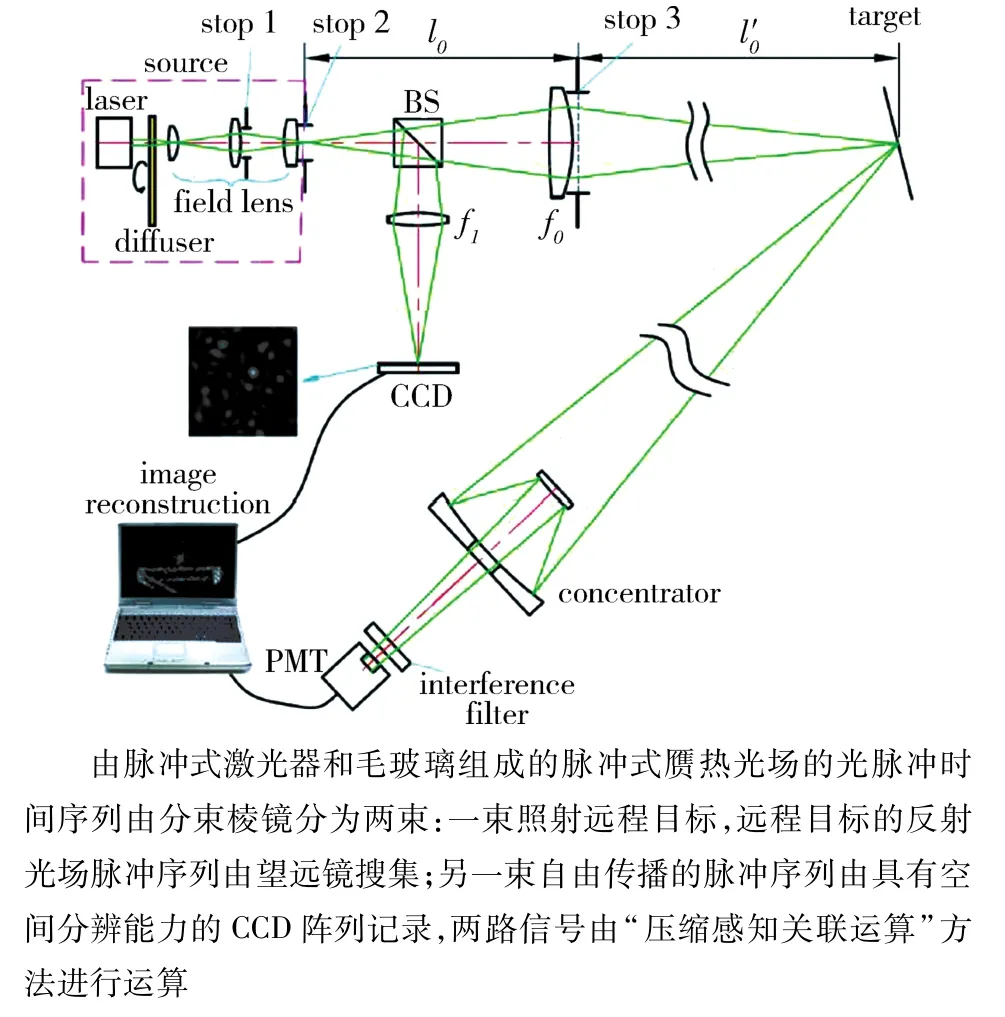
图20 遥感鬼成像装置图Fig.20 The setup for remote sensing ghost imaging

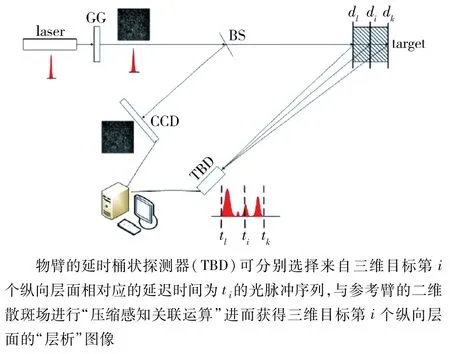
图22 三维鬼成像原理图Fig.22 The setup for 3D ghost imaging

2 大气湍流中的关联成像

大气湍流的直接后果是导致折射率的随机起伏.这不仅使得光束在传播过程中发散，而且会引起闪烁进而使得接受器受到的信号受噪音的干扰.如何抵抗大气湍流对成像以及光信息传输的不利影响，一直是学界的兴趣所在［63］.那么对于鬼成像而言，湍流将造成什么样的影响？相较于传统成像，鬼成像在湍流中的表现有何不同？有没有超越传统成像的优点？这也是近年来的研究热点.这方面的研究大致可分为5个方面（见2.1～2.5），其中主要集中于基于大气湍流导致光场相干性改变的研究（见2.1）.

2.1 基于大气湍流导致光场相干性改变的研究真空中，光场的相干性可以用交叉谱密度函数［64］表示

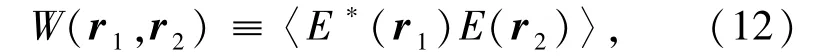
通常具有高斯-谢尔模的形式［64］，即

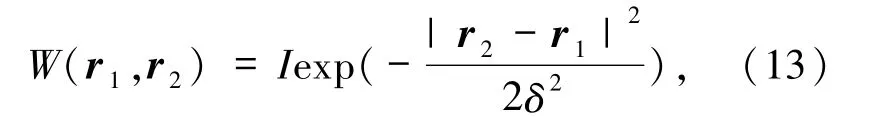
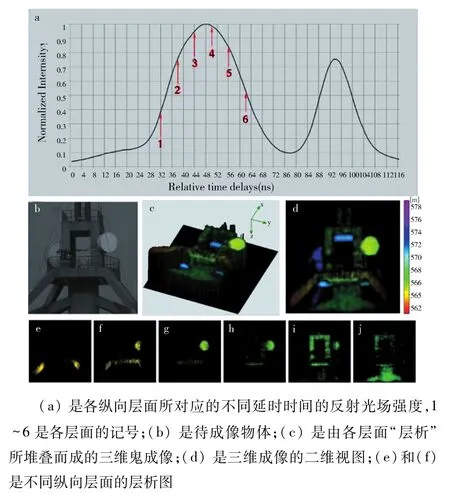
图23 三维单像素鬼成像Fig.23 Single pixel 3D ghost imaging

其中，r1＝ （x1，y1）和r2＝ （x2，y2）为垂直与传播方向任一平面上的亮点，δ为真空中光场的横向相干长度（以下简称相干长度），用以衡量光场的横向相干性（以下简称相干性）.而湍流导致的折射率改变，将使得（12）式中的 E（r1）和 E（r2）额外附带相位 Ψ（r1）和 Ψ（r2），这使得（12）式变为［63］

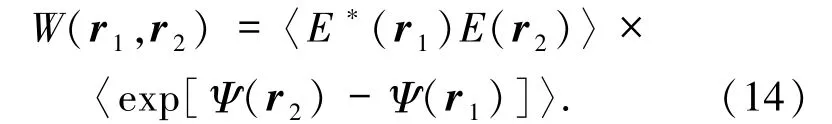
湍流理论［63］表明

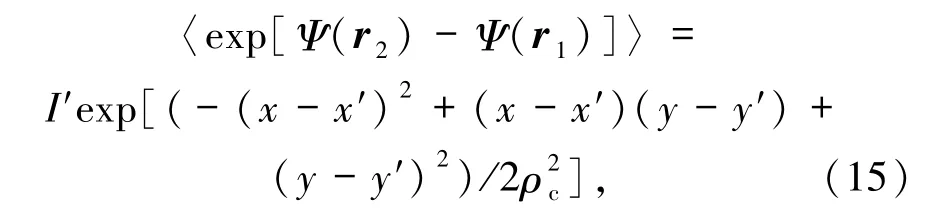
在有些报道（如文献［65］）中上式也可写为

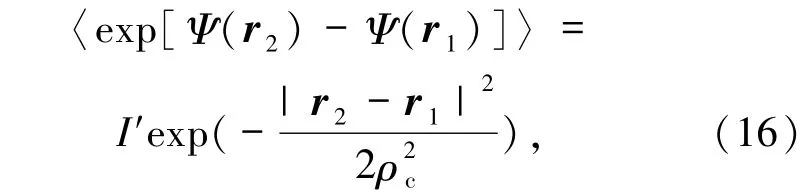
其中，ρc＝，为湍流介质的球面波的相干长度，是折射率结构常数.综合（14）和（16）式为例，可以看出（12）式将不再是真空中的（13）式，最突出的变化是相干长度由δ变短为

以上内容结合部分相干光束的传输公式，如最常见的科林斯积分［66］

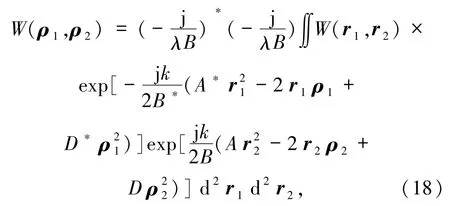
构成这部分研究的理论基础，其中的参数A、B、C、D为光场传输矩阵各矩阵元.

2009 年，Han 团队［67］和 Cheng［68］预言成像系统点扩散函数的宽度与大气的湍流强度与成像距离以及光源大小有关，前二者的增加以及后者的减小将导致成像系统的点扩散函数变宽，因而成像质量将逐渐劣化.而Han团队［67］则理论上更是对比了大气湍流对普通成像和鬼成像的影响，表明鬼成像相较于普通成像，具有更好的抵抗湍流对像质的劣化作用.上述研究，均假设经典热光场是完全非相干的.2010年，Pu等［69］研究了部分相干光在湍流大气中成像的性质.他们的研究结果除与上述研究中有关湍流强度、传输距离，以及光源的大小对像质的影响的结论一致外，还得到光场的相干性与成像质量的关系，即横向相干尺度越小，即横向相干性（以下简称相干性）越差，成像的质量越好.

2011年，Boyd及同事［65］针对湍流介质在物臂中具体的位置以及纠缠光源位置偏移，研究了导致成像对比度的改变的几个因素.在图24［65］所示的光路的参考臂中，湍流介质分别位于NLC晶体-透镜（Lens）之间，以及位于透镜（Lens）-物体（Object）之间.他们把图 24［65］的装置图“等价”为图 25［65］所示的鬼成像 Klyshko 图景［70］.研究表明，当湍流介质处于上述2种位置的任何一种时（见图25［65］上半部分和下半部分），鬼成像的分辨率均可表达为

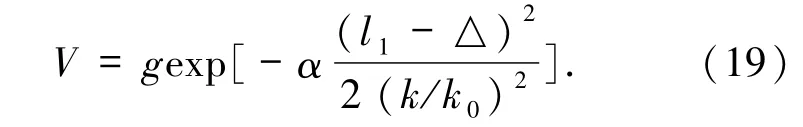
（19）式适用于对此2种情况鬼成像的描述，即湍流程度越大，成像的分辨率越低；湍流介质越靠近透镜，成像的分辨率也越低.同年，他们对在如图24［65］所述鬼成像架构下，湍流介质位于参考臂的情形进行了研究［71］.此时的湍流位置仍分成介于参考臂探测器（SPAD）-透镜之间，和介于透镜-NLC晶体之间.对此2种情况，系统的点扩散函数宽度为

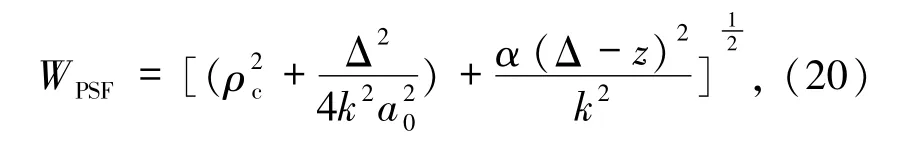
其中，Δ-z是探测器到湍流介质的距离；当湍流介质介于透镜-NLC晶体之间时，Δ-z是透镜到湍流介质的距离，这2个距离越大，点扩散函数越宽，成像的清晰度则越差.由此可见湍流介质处于物臂时和处于参考臂时对成像分辨率的影响［65］的区别.

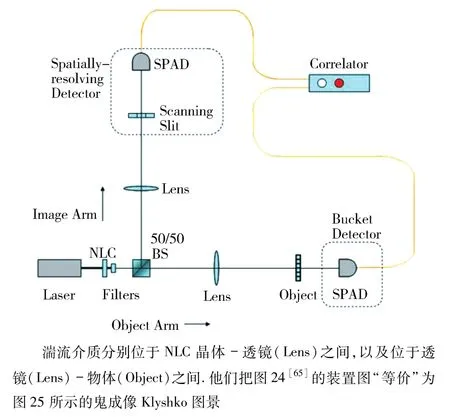
图24 湍流对鬼成像与经典成像影响对比研究Fig.24 The setup for investigating effects of turbulence on ghost imaging and classical imaging comparatively

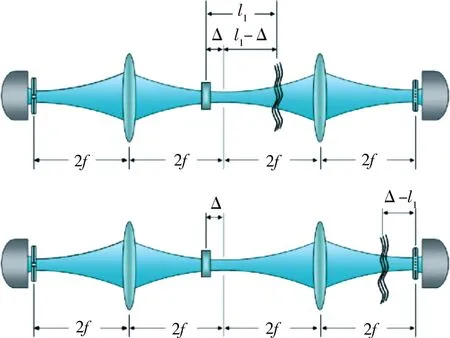
图25 图24所涉鬼成像架构的Klyshko等效图景Fig.25 Klyshko picture for ghost imaging shown in Fig.24

2013年，Cheng等［72］给出鬼成像和鬼衍射在大气湍流中的统一理论，研究了大气湍流的强度、光源的大小、光源相干性，以及物臂探测器尺寸对成像的影响.他们的研究表明，相较于鬼衍射，鬼成像具有更好的抗湍流影响的能力.同时，研究中也籍由对比鬼成像与传统成像在大气湍流中的区别，讨论了鬼成像是否能免于大气湍流影响的问题（见2.2）.

2018 年，Bai等［73］研究了湍流中倾斜摆放的物体的鬼成像.研究发现，在中等湍流的前提下，物体的倾斜程度对成像的质量影响并不大，但鬼成像的质量要优于直接成像；在强湍流的前提下，倾斜将对成像质量造成重大影响，且鬼成像的质量仍优于直接成像；2012年，Zhang等［74］研究了大气湍流对“计算鬼成像”的影响.他们的解析结果表明成像距离、成像系统的孔径角大小、湍流功率谱的非柯尔莫戈罗夫分形常数共同影响成像质量.同年，Zhang等［75］研究了用多高斯谢尔光束作为照明光源的鬼成像，分别展示了不同光源面积、不同横向相干长度，以及不同湍流程度下的鬼成像理论结果.结果显示，光源面积的增大、横向相干长度，以及非柯尔莫戈罗夫谱的幂律指数的增大均导致成像质量的提高.

2.2 利用鬼成像消除或减轻大气湍流的不利影响2011年，Shi小组［76］实验观察到鬼成像在一定条件下可免于湍流影响；同年，MIT的 Shapiro等［77］研究了反射式物体在湍流中的鬼成像.他们的研究对象分别为：由旋转毛玻璃产生的高斯-谢尔光源的鬼成像、由参量下转换提供的纠缠光源的鬼成像，以及计算鬼成像.他们就上述3种鬼成像的分辨率、对比度，以及系统信噪比得出解析结论：尽管湍流存在，但上述3种鬼成像在一定条件下，均可不受湍流影响.2012年，Shi团队［78］分别选取桶状探测器中高于和低于平均值的数据与CCD阵列信号进行鬼成像的关联运算，前者称之为“正像”［79］，后者称之为“负像”［79］，发现这2种像均可不被湍流劣化.2018年，Shi团队［80］发表了与大气湍流中鬼成像机理相近的HBT实验，仍得到湍流的影响可以消除的结论.

值得一提的是Cheng等［72］在2013年提出的鬼成像和鬼衍射在大气湍流中的统一理论（见2.1节）的研究中，也讨论了鬼成像是否能免于大气湍流影响的问题.他们的研究结论是：

1）鬼成像（见图 26［72］（a））与传统成像（见图 26［72］（b））均受大气湍流的影响；

2）湍流中以参考臂x1为坐标的鬼成像（见图 26［72］（a））表达式为

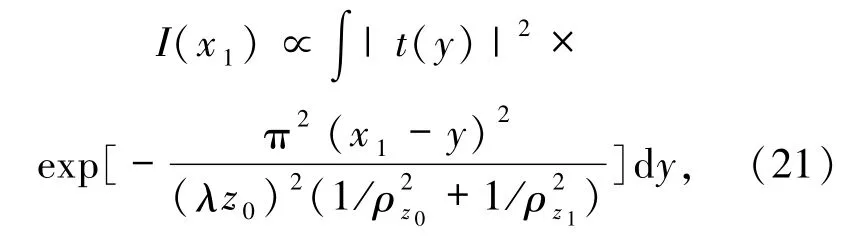
其中，ρz0和ρz1分别表示光源到物体之间的光路以及光源到参考臂探测器之间的光路的球面波湍流传播相干长度.由（21）式可见，决定鬼成像分辨率的点扩散函数的展宽因素来自光源到物体之间的光路以及光源到参考臂探测器之间的大气湍流；

3）湍流中以 x2为坐标的传统成像（见图 26［72］（b））表达式为

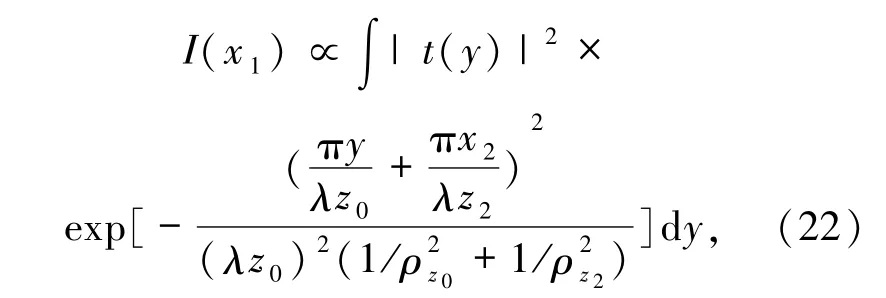
其中，ρz0和ρz2分别表示物体到透镜之间的光路以透镜到成像面之间的光路的球面波湍流传播相干长度.由（22）式可见，决定传统成像分辨率的点扩散函数的展宽因素来自这两部分大气湍流.

对比以上的2）和3）可知，由于计算鬼成像省略了参考臂，z0部分的湍流影响将消除（图26［72］（a））.而湍流对物臂光路的影响也仅限于物体前方光路，物体后方光路的湍流对成像没有影响.另一方面，对于传统成像（图26［72］（b）），从物体后方到透镜前方，以及从透镜后方到探测面前方所有光路中的湍流都对成像造成影响.因此计算鬼成像抵御大气湍流影响的能力可以优于传统成像.

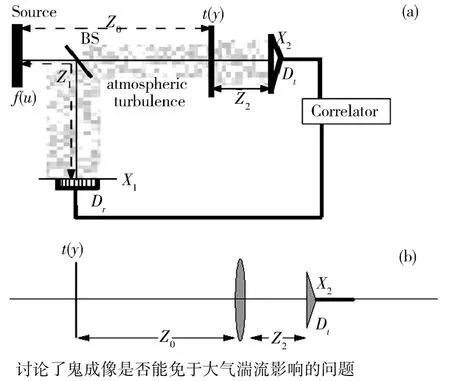
图26 鬼成像和鬼衍射在大气湍流中的统一理论Fig.26 Unified theory of thermal ghost imaging and ghost diffraction through turbulent atmosphere

2.3 基于散射理论的研究 2011年，Han团队［81］对沉浸在散射液体中的物体进行了鬼成像研究.他们给出了成像的数学模型，即物臂系统的点扩散函数 h（x，x0）是自由传播的点扩散函数hin（x，x0）与包含散射过程点扩散函数hsca（x，x0）的加权叠加，即

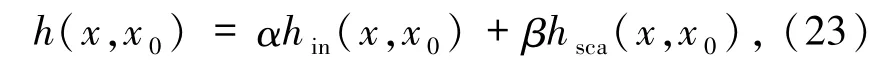
其中，α和β是权重因子.而包含散射过程的点扩散函数hsca（x，x0）则为由光源到散射介质内部的点扩散函数P（x′，x0）与散射介质内部到探测坐标自由传播的点扩散函数 hin（x，x′）的积分变换，即

依据该模型，他们对物体在散射液体中不同摆放位置的成像情况进行了数值模拟和实验上对比.研究表明，对于物体到物臂探测器经历的散射介质越长，直接成像质量越差，而鬼成像质量则越好.同样条件下的鬼成像，参考臂使用点探测器要比使用桶装探测器的成像质量高.这项研究虽然数学模型与2.1 节不同，但对照 2.2 节［72］的研究结论可知，对于鬼成像，关于物体后方散射介质对成像质量的影响，与湍流介质是一致的.

2015年，Liu等［82］对比了光路中含有散射介质的直接成像和鬼成像的情况.研究表明（图27［82］），随着散射强度的增加，直接成像与鬼成像的均方根噪声都增大，但直接成像随散射强度的增大幅度要比鬼成像大得多.另一方面，随着散射强度的增加，直接成像与鬼成像的信噪比都将衰减，而直接成像的信噪比衰减程度度要比鬼成像大得多.由此表明散射介质中鬼成像要比传统成像更能够获得高质量的图像.

图27 （a）～（f）不同的散射强度所对应的鬼成像（左）和直接成像（右）Fig.27 （a）～ （f）Different scattering strengths and their related ghost imaging （left）and direct imaging （right）

另外，2016 年，Li等［83］研究了光路中包含强散射介质的鬼成像.他们发现，当强散射介质位于物臂时，依然能得到清晰的图像；但当位于参考臂时，则图像将被劣化，直至得不到图像.该结论也与前述湍流介质中鬼成像［72］的结论一致.

2.4 基于调制光源形状的研究 2012年，Shi团队［84］对比了随机Bessel光束和随机高斯光束的“虚拟鬼成像”（即如1.4节所述参考光预先由计算机设定，信号光则由无空间分辨率的的桶状探测器获取的鬼成像，也称“计算鬼成像”或“单像素成像”）.实验表明，相较于随机高斯光束，随机Bessel光束对于湍流或模糊介质中的物体成像具有更高的分辨率.

2015年，Cheng等［85］理论研究了光源强度为“多双曲余弦高斯函数”

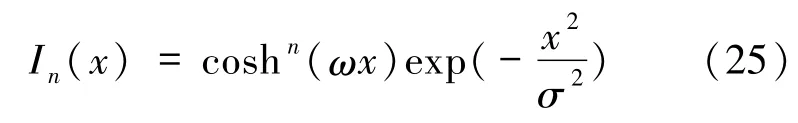
的完全非相干照明下的鬼成像.研究表明光场的传输距离z、Cn，连同双曲余弦光源参数ω、σ，以及光源阶数n均对成像的点扩散函数造成影响，其中z、Cn的增大导致点扩散函数变宽，进而使成像质量劣化，而光源参数ω、σ，以及光源阶数n的增加将导致点扩散函数变窄，增强成像质量，进而抵御大气湍流的影响.2017年，Luo等［86］继续采用同样方法对大气中鬼衍射得到的结论与之前鬼成像研究［85］一致.

2.5 基于双波长光源的研究 2013年，Shi团队［87］研究了在物臂和参考臂中使用2种不同波长的经典热光场照明的情形.他们的理论计算表明，在物臂中使用较短波长和在参考臂中使用较长波长的光场照明，有助于抵抗湍流对成像质量的影响.他们还研究了计算鬼成像的情形，数值结果表明较短波长照明有助于抵抗湍流对成像质量的影响.稍早一年，他们曾在鬼成像物臂加入自适应光学系统，用以抵消湍流引起的相位畸变［88］.数值研究研究表明，应用自适应光学系统可以提高成像质量.2013年，She等［89］数值研究了采用不同波长的信号光和参考光的大气鬼成像，得到类似文献［87］的结果.

与上述观点不完全相同的是，2014年，Zhang等［90］研究的由参量下转换获得的纠缠光源大气双波长凝视鬼成像.他们得到如下的结论：对于强湍流，物臂使用波长较长的光束而参考臂使用波长较短的光束有助于提高成像的分辨率；对于弱湍流，物臂使用波长较短的光束而参考臂使用波长较长的光束有助于提高成像的分辨率.由于波长较长的光束能很好的克服大气对光波的吸收，因而上述第一点特别适合强湍流、强吸收条件下的凝视鬼成像.

2.6 其他 2012 年，加州工学院 Erkmen［91］研究了湍流中“计算鬼成像”，报道了物体光路上的非柯尔莫戈罗夫功率谱湍流导致的成像分辨率的研究.研究表明，短时间曝光的平均值所成的像可以减轻大气湍流对成像分辨率的影响.从理论上论证计算鬼成像在湍流中的分辨率优于传统的成像分辨率.

2016 年，Cheng等［92］认为，降低鬼成像的数据采集过程的时间，可以减轻大气湍流对成像的影响.为此他们采取了减少光源像素、像素随机分配，以及增加探测器数量以形成“多桶状探测器”的方法，以加快数采速度.上述经由压缩采样的数据经由稀疏复原算法，得出的最终成像结果与关联计算得到结果对比显示，前者具有更好的成像质量.2013年，Zhao等［93］研究了大气中角动量纠缠的“全息鬼成像”.折射率结构常数Cn的加大会影响成像质量；针对此现象，Zhao等［94］于同年采用Reed-Solomon编码方法改善了因大气湍流而导致的成像质量劣化.

3 小结与展望

本文回顾了关联成像，尤其是鬼成像的研究起源、历程、研究进展，以及在一些领域的应用.与传统成像相比，鬼成像远不止异于常识的“鬼特性”，而是具有传统成像难以替代的优势和潜力.本文分别介绍关联成像在光学相干和偏振领域、单像素成像、物体的复值获取、超越经典分辨率、X射线衍射成像、激光雷达等领域的应用，以及带给这些领域的突破和进展.作者在这些诸多的领域中，对大气湍流领域进行了详细的阐述.

近年来，光场调控受到越来越多研究人员的关注，已逐渐成为光学领域的热点研究课题之一.光场的多维调控，包括振幅、相位、偏振、相干性等的方法和技术越来越成熟，这些特殊调制在关联成像领域是值得重点研究的一个课题.利用调控光束的某些特性和关联成像相结合解决光学中的逆反问题更是引发作者的期待.