inf-αR合成Fuzzy关系方程的解集

杨 雪， 吴 莉， 王学平*

（1.四川师范大学数学与软件科学学院，四川成都610066；2.阿坝师范学院数学与计算机科学学院，四川汶川623002）

1 引言及预备知识

Fuzzy关系方程是由法国学者 Sanchez［1］于1976年率先研究的.随后，众多的研究工作者投入到这个研究领域，详细研究工作可参考文献［2-12］.1985 年，Di Nola等［13-14］发现用inf-α 型合成算子去进行Fuzzy关系的计算或推理规则的合成效果会更好，并提出了inf-α合成Fuzzy关系方程的研究.之后，李裕梅等［15］在完全并既约元的条件下研究了inf-α合成Fuzzy关系方程AαX＝b有解的条件.李裕梅等［15-18］给出了完备 Brouwer格 L上inf-α合成有限模糊关系方程RαX＝A有解的充要条件，并刻画了解集.2005年，Yang等［19］研究了［0，1］格上模糊关系R的 α分解问题，给出了使AαB＝R成立的所有（A，B）构成的集合，并由此给出了可α分解的矩阵收敛指数的算法.向太阳等［20-21］推广了模糊关系R的α分解问题，研究了模糊关系R的αR分解问题，给出了使AαRB＝R成立的所有（A，B）构成的集合，给出了可αR分解的矩阵收敛指数的算法.本文对定义在［0，1］上infαR合成Fuzzy关系方程RαRX＝A的解集问题进行了讨论.首先对方程 RαRX ＝a（其中，a∈［0，1］）进行了讨论，构造出了RαRX＝a的所有极大解并确定了整个解集，进一步构造出了方程RαRX＝A的整个解集.

定义 1.1［1］称映射 A：X→［0，1］为 X 上的Fuzzy集，记 F（X）＝｛A｜A：X→［0，1］｝.称映射 R：X×Y→［0，1］为X ×Y上的 Fuzzy关系，记 F（X ×Y）＝ ｛R｜R：X ×Y→［0，1］｝.

设 R∈F（X ×Y），令MR＝max｛R（x，y）｜x∈X，y∈Y｝.

定义 1.2 设 R∈F（X ×Y），a，b∈［0，1］，定义二元算子 αR：［0，1］×［0，1］→［0，1］满足

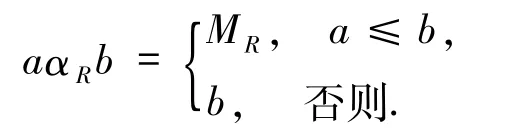
由定义1.2有下面的定理成立.

定理 1.1 设 R∈F（X ×Y），则：

1）∀a，c∈［0，1］，b∈［0，MR］，如果 b≤c，则aαRb≤aαRc；

2）∀a∈［0，1］，b∈［0，MR］，b≤aαR（a∧b）；

3）∀a，c∈［0，1］，b∈［0，MR］，aαR（b∧c）＝（aαRb）∧（aαRc）；

4）∀a，b∈［0，1］，a∧（aαRb）≤b；

5）∀a，c∈［0，1］，b∈［0，MR］，a∧b≤c当且仅当 b≤aαRc.

证明 1）如果 a≤b≤c，则 aαRb＝MR，aαRc＝MR，所以 aαRb≤aαRc；如果 b≤c＜ a，则 aαRb＝ b，aαRc＝ c，所以 aαRb≤aαRc；如果 b ＜ a≤c，则aαRb＝b，aαRc＝MR，由 b≤MR知，aαRb≤aαRc.

2）对∀a∈［0，1］，b∈［0，MR］，如果 a≤b，则aαR（a∧b）＝aαRa ＝ MR≥b，即 b≤aαR（a∧b）；如果a＞b，则aαR（a∧b）＝aαRb＝b成立.

3）由1）即知.

4）对∀a，b∈［0，1］，如果 a≤b，则 aαRb ＝MR，所以 a∧（aαRb）＝a∧MR≤b成立；如果 a ＞b，则 aαRb＝b，所以 a∧（aαRb）＝a∧b＝b≤b成立.

5）充分性 设 a∧b≤c，如果 a≤a∧c，则 a≤c，那么由 b∈［0，MR］可知 b≤MR＝ aαRc.如果 a ＞a∧c，则 b≤c＜a.所以 b≤aαRc＝c成立.

必要性 如果b≤aαRc，由定义1.2 即知a∧b≤c.

注 1.1 一般情况，定理 1.1 的 1）、2）、3）和5）中条件 b∈［0，MR］不能去掉.

例 1.1 设 R∈F（X ×Y），MR＝0.7，则：

1）设 a ＝0.85，b＝0.8，c＝0.9，则aαRb＝0.8，aαRc＝0.7，因此 aαRb＞aαRc；

2）设a ＝0.5，b＝0.9，则 aαR（a∧b）＝aαRa＝MR＜b；

3）设 a ＝0.9，b＝0.8，c＝1，则 aαR（b∧c）＝aαRb＝0.8，而（aαRb）∧（aαRc）＝ （0.9αR0.8）∧（0.9αR1）＝0.8∧0.7 ＝0.7；

4）设 a＝0.6，b＝0.8，c＝1，则 a∧b≤c成立，但 b＞aαRc.

定义 1.3 设 R ＝ （rij）I×J，A ＝ （ai）i∈I，X ＝（xj）j∈J，称

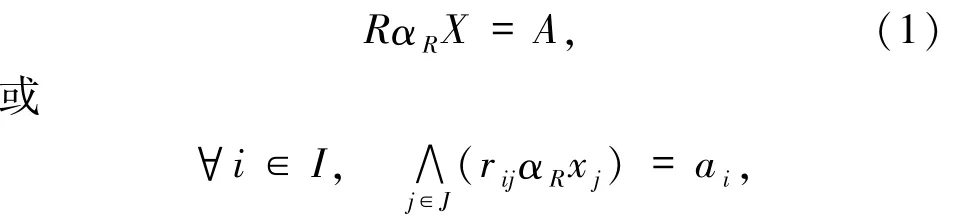
为定义在［0，1］上的inf-αR合成Fuzzy关系方程，且 rij，ai∈［0，1］.xj∈［0，1］是未知的，I与 J 为指标集.如果X使RαRX＝A成立，则称X为inf-αR合成Fuzzy关系方程的解，记为 X1＝｛X｜RαRX＝A｝，称X1为方程RαRX＝A的解集.

显然，方程（1）的一个特殊形式为

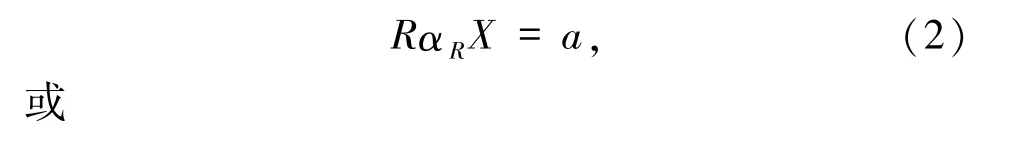
记 X2＝ ｛X｜∧j∈J（rjαRxj）＝ a｝.

命题 1.1［14］如果 X1，X2∈X1且 X1≤X≤X2，则 X∈X1.

证明 仅证 X1，X2∈X1的情况.设 X1＝）j∈J，X＝ （xj）j∈J，X2＝）j∈J.下面分3种情况讨论.

1）如果任意 j∈J，xj∈［0，MR］，则由 X1，X2∈X1，X1≤X≤X2及定理 1.1 的 1）知，对任意 i∈I，

定义 1.4［22］设 P 为一偏序集，a∈P，若不存在x∈P使得x＞a，则称a为P的极大元.

定义1.5 称所讨论的inf-αR合成Fuzzy关系方程的解集中的极大元（如果存在）为所讨论的inf-αR合成Fuzzy关系方程的极大解.

注1.2 设X*∈X1（X1为所讨论的 inf-αR合成Fuzzy关系方程的解集），则由定义1.5知，X*是X1的极大元当且仅当任取X∈X1，如果X≥X*，则 X＝X*.

本文所讨论的Fuzzy集和Fuzzy关系均定义在［0，1］上.众所周知，Fuzzy关系可用 Fuzzy矩阵来表示，故对于给定的R∈F（X×Y），以下R既表示X×Y上的一个Fuzzy关系，也表示X×Y上的一个Fuzzy矩阵.

2 方程（1）和（2）相互间的关系

定理 2.1 设 R ＝ （rj）j∈J，

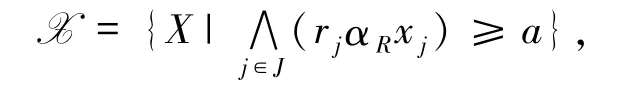
则X≠Ø当且仅当a≤MR.

必要性 如果 a≤MR，设 X ＝ （MR）j∈J，则 X∈X，即X≠Ø.

显然，X2⊆X.设 R ＝ （rj）j∈J，a∈［0，1］，定义R⊙a ＝ （rj∧a）j∈J.

定理 2.2 设 R ＝ （rj）j∈J，则 X2≠Ø当且仅当X*2＝R⊙a∈X2.进一步，X*2＝R⊙a是 X2的最小元.

证明 1）首先证明X≠Ø时，X*2∈X，且X*2是X的最小元.

如果X≠Ø，则由定理2.1知a≤MR，那么对∀j∈J，如果 rj≤a，则rjαR（rj∧a）＝ MR，即 rjαR（rj∧a）≥a；如果 rj＞ a，则 rjαR（rj∧a）＝ rjαRa ＝ a.所以

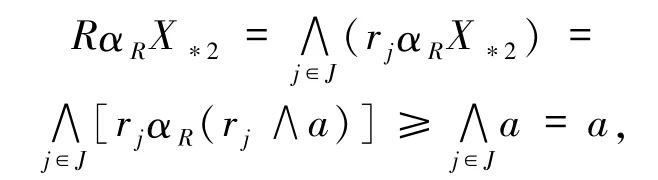
即X*2∈X.又设 X ＝ （xj）∈X，则 RαRX≥a，即（rjαRxj）≥a，那么对任意 j∈J，rjαRxj≥a.因为a≤MR，由定理 1.1 的 5）知 xj≥（rj∧a），即 X≥X*2.由X的任意性知X*2是X的最小元.

2）再证X2≠Ø当且仅当X*2＝R⊙a∈X2.

充分性 如果X2≠Ø，则X≠Ø.设X＝（xj）∈X2⊆X，则 X∈X，那么由 1）知 X≥X*2.又由定理 2.1知 a≤MR，因此∀j∈J，rj∧a≤MR.所以由定理 1.1 的 1）知 a ＝RαRX≥RαRX*2≥a，即RαRX*2＝a，所以 X*2＝R⊙a∈X2.显然，X*2＝R⊙a是X2的最小元.

必要性 显然成立.

由定理2.2可知下面命题成立.

命题2.1 rαRx＝a有解当且仅当r∧a是它的解，且r∧a是rαRx＝a的最小解.

记 Ri＝ （rij）j∈J为 R ＝ （rij）I×J的第 i行向量，Xi2＝ ｛X｜RiαRX ＝ ai｝.

定理 2.3 1）X1≠Ø当且仅当Xi2≠Ø，且X1＝Xi2.

2）X1≠Ø当且仅当 X*1＝（Ri⊙ai）是 X1的解.进一步，任取 X∈X1，X≥X*1.

证明 1）显然.

2）设 X ＝ （xj）j∈J∈X1，于是对任意 i∈I，（rijαRxj）＝ ai.于是由定理 2.1 知 ai≤MR.又由定理 2.2 知，X≥Ri⊙ai，因此 X≥（Ri⊙ai）＝X*1.因为对任意 i∈I，j∈J，（rij∧ai）≥（rij∧ai），所以由定理 1.1 的 1）与 2）知，任意 i∈I，j∈J，rijαR［（rij∧ai）］≥ rijαR（rij∧ai）≥ ai.又对任意j∈J，

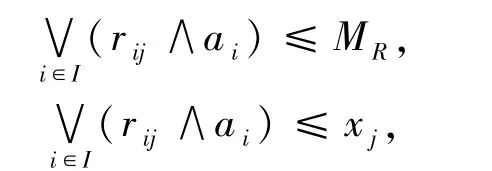
所以由定理1.1 的1）知，对任意 j∈J，

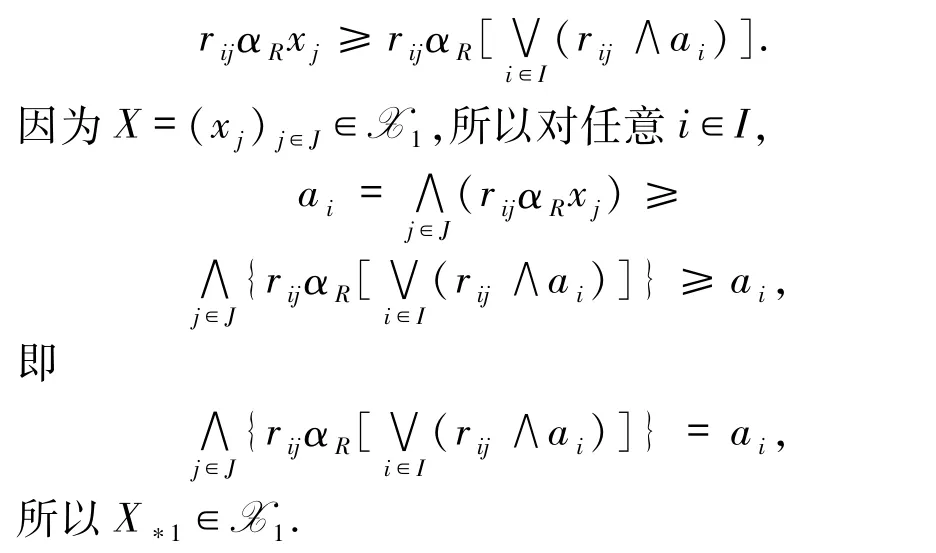
3 方程（2）有解的充要条件与极大解问题

定理 3.1 X2≠Ø当且仅当G（a）≠Ø.

证明 充分性 如果X2≠Ø，设X＝ （xj）j∈m∈X2，于是（rjαRxj）＝ a，因此存在 j∈m使a＝rjαRxj. 由 命 题 2.1 及 定 理 1.1 知 a ＝rjαR（rj∧a）＝rjαRa，即 j∈G（a），所以G（a）≠Ø.

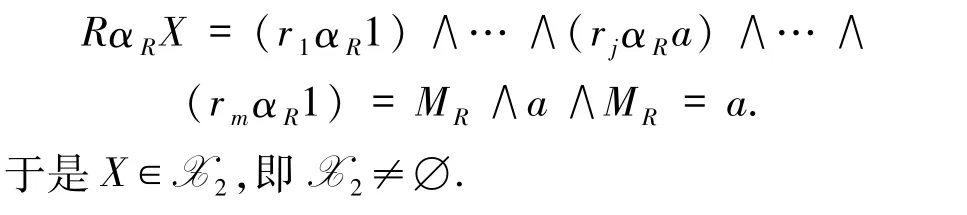
注 3.1 当 a＝MR时，易见 G（a）＝.令X*＝（1，1，…，1）T，则 X*∈X2.再由命题1.1与定理2.2知，此时 X2＝［（R⊙a）T，X*］.

以下假设方程（2）中a≠MR.

定理 3.2 如果 X2≠Ø，∀j∈G（a），定义为：∀k

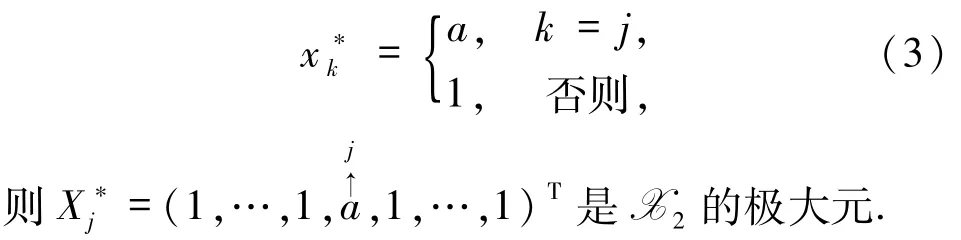
证明 如果X2≠Ø，由定理3.1的证明知，∈X2.接下来只须证在X2中的极大性.假设X∈X2且X≥，则当 i≠j时，显然 xi＝＝1；当i＝j时，由X≥知 xj≥a.又因为 X∈X2，所以

a ＝ RαRX ＝ （r1αR1）∧… ∧（rjαRxj）∧… ∧

（rmαR1）＝ MR∧（rjαRxj）∧MR＝ rjαRxj，即 a ＝rjαRxj.因为 a≠MR，所以由定义 1.2 知 xj＝a，即 X ＝，由注1.2 知是X2中的极大元.

定理3.3 如果X2≠Ø，则X2的每一个极大元都具有（3）式的形式.进一步，X2有｜G（a）｜个极大元.

定理3.4 如果X2≠Ø，则任意X∈X2，存在X2中的极大元，使≥X.证明 设X＝，于是 a＝RαRX ＝），则存在使得 a ＝ rjαRxj，由定理3.2的证明知 xj＝ a.设＝ （1，…，1，1，…，1）T，则X.又由定理3.2 知，是X2的极大元.

由定理2.2、定理3.3、定理 3.4 及命题 1.1 易证下一定理.

定理3.5 如果X2≠Ø，则

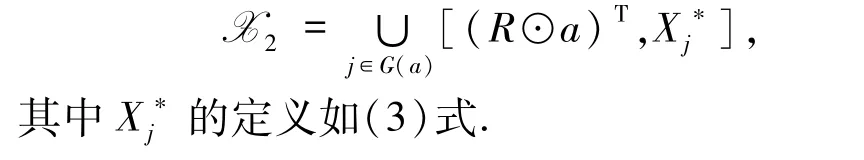
例 3.1 已知 R ＝ （0.6，0.8，0.7），a ＝0.63，求解inf-αR合成Fuzzy关系方程RαRX＝a.

由定理3.5知方程RαRX＝a的解集为

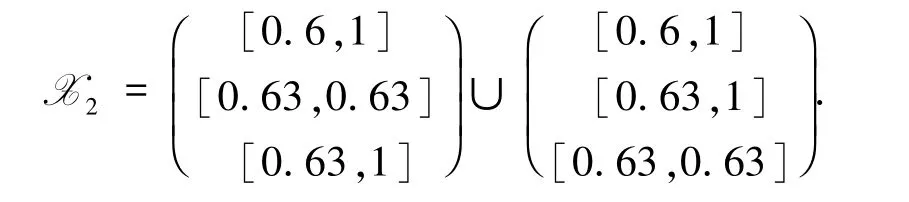
4 方程（1）的解集

下面将证明方程（1）的每个解都有大于或等于它的极大解，并给出方程（1）的解集构造.

定理 4.1 如果 X1≠Ø，则 M ＝ ｛X｜X＝∈Mi是X1的一非空有限子集，且X是M的极大元当且仅当X是X1的极大元.

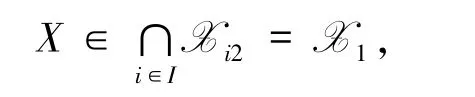
所以M⊆X1.又因为M关于Fuzzy包含“≤”是一个有限偏序集，所以M有极大元.

设X*是M中的极大元且存在X∈X1使X≥X*.于是由定理2.3知任取，X∈Xi2.所以由定理3.4 知，任取，Xi2中有极大元使≥X≥，所以∈M，由X*在M中的极大性及≥X≥X*知X＝X*.因此X*也是X的极1大元.

反过来，设X*是X1的极大元.因为M⊆X1，要证X*也是M中的极大元，则只需证X*∈M即可.事实上，由定理2.3的1）知，任取，X*∈Xi2.所以由定理3.4 知任取，存在 Xi2的极大元 Xi使 Xi≥X*≥X*1，所以≥X*，且M.因此∈X1.由 X*在 X1的极大性知，＝X*，所以 X*∈M.

定理4.2 如果X1≠Ø，则任取X∈X1，存在X1的极大元X*使X*≥X.

证明 设 X∈X1，由定理2.3 的1）知，任取i∈，X∈Xi2，因此由定理 3.4 知，任取，存在∈M使≥X.设 M*＝，则M*∈M.i

进一步，由定理4.1知，一定存在M中的极大元M使M≥M*，又因为M*≥X，因此存在X1的极大元M使M≥X.

定理4.3 如果X1≠Ø，则

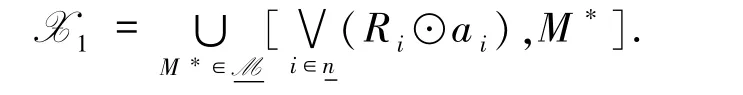
例 4.1 已知

求解inf-αR合成Fuzzy关系方程RαRX＝A.

解 易得

所以，由定理3.2知方程R1αRX＝a1的极大解为

故由定理4.3得