max-*合成模糊关系方程的解集

朱晓庆， 熊清泉

（四川师范大学数学与软件科学学院，四川成都610066）

模糊关系在模糊系统中占有比较重要的地位，模糊关系方程为模糊关系的主要研究对象之一.1976 年，Sanchez［1］首先讨论了 max-min 合成有限模糊关系方程，给出了方程有解的判定定理，并且在有解情况下给出了最大解的公式.之后，大量的研究者从不同合成算子、不同论域、不同算法等方向来研究模糊关系方程［2-10］.值得注意的是，Zhao［11］在完备分配格上讨论了矩阵方程，当格中每个元都有不可约有限并（交）既分解时，给出了方程可解的充要条件，并且在方程可解时，进一步给出方程的解集.1989年，Di Nola等［12］讨论了完备Brouwer格上max-min合成模糊关系方程，给出了方程有解的充要条件.De Baets［13-14］讨论了完备分配格上的sup-T合成模糊关系方程，其中T为t-模.Fodor等［15］证实非交换、非结合算子在近似推理中更有效.2005年，Wang等［9］讨论了完备格上的sup-T合成模糊关系方程，其中T为伪t-模（非交换、非结合），给出了方程有解的充要条件以及存在极小解的充分条件，获得了相应的解集结构.事实上，在求解sup-T（T代表t-模或伪t-模算子）合成模糊关系方程时，求极小解是其中的关键.针对不同合成算子，研究者给出了不同求极小解的方法.Lin［4］用覆盖方法研究了max-Archimedean t-模合成模糊关系方程，发现此类方程与无冗余覆盖存在一一对应关系.Han等［3］在方程有解时根据最大解构造有限偏序集，进一步求出方程的极小解.Matusiewicz等［16］在求解max-*合成模糊关系方程时，通过诱导矩阵首先求出不等式的极小解，进而得到方程的极小解.本文在文献［16］基础上不引入诱导矩阵，讨论［0，1］上max-*合成模糊关系方程.首先讨论单个变量方程，给出方程有解的充要条件.然后讨论多变量单一方程，给出方程解集非空的充要条件.在解集非空时，进一步给出方程存在极小解的必要条件以及极小解的个数.最后讨论方程组的解集，给出方程组解集非空的充要条件，并且在方程组解集非空时，利用最大解构造有限偏序集的方法给出方程组的极小解，进一步给出方程组的解集.

1 预备知识

设 I ＝ ｛1，2，…，m｝，J ＝ ｛1，2，…，n｝.向量 x＝ （xj）j∈J，y ＝ （yj）j∈J，矩阵 A ＝ （aij）I×J，B ＝（bij）I×J，其中，xj，yj，aij，bij∈ L ＝ ［0，1］.定义序关系≤为 x≤y⇔xj≤yj，A ≤ B⇔aij≤bij，∀i∈ I，j∈ J.

考虑方程

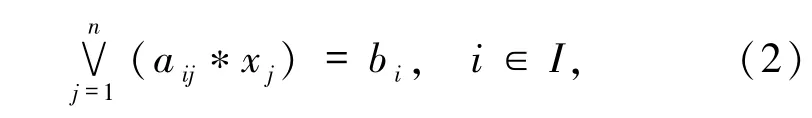
其中“◦”代表 max-*合成运算，矩阵 A ＝ （aij）m×n与向量 B ＝ （bi）i∈I已知，X ＝ （xj）j∈J未知.

定义 1.1［17］设T ：L ×L→L满足：∀a，b，c∈L，有

（i）交换律：T（a，b）＝ T（b，a）；

（ii）结合律：T（a，T（b，c））＝ T（T（a，b），c）；

（iii）单调性：如果 b≤c，则T（a，b）≤T（a，c）；

（iv）有界性：T（a，1）＝ a，称T是（L，≤）上的三角模（简称t-模）.

定义1.2［18］设Γ：L ×L→L满足：∀a，b，c∈L，

（i）单调性：如果b≤c，则Γ（a，b）≤Γ（a，c）；

（ii）边界条件：Γ（1，a）＝ a且 Γ（0，a）＝ 0，称Γ是（L，≤）上的伪t-模.如果Γ还满足Γ（a，0）＝0，则称Γ为强伪t-模.

定义 1.3［17］设二元运算*：L × L →L，如果对任意单调不减的序列｛xn｝n∈N都有（xn*y））*y，∀y∈L，则称二元运算*是左连续的.类似可定义右连续，如果*既是左连续的也是右连续的，则称*是连续的.

定义 1.4［16］设*：L ×L→L 满足：∀a，b，c∈L，

（i）单调性：如果 b≤ c，则 a*b≤ a*c；

（ii）边界条件：1*0 ＝0；

（iii）连续性：既是左连续的也是右连续的，称*是（L，≤）上的*运算.（L，≤）上的全体*运算用LRC表示.

定义 1.5［19］设φ：L × L→L，定义→φ与←φ为：∀a，b∈ L，

假定空集的上确界是0，下确界为1.特别地，当φ＝*时，二元运算→*：L×L→L称为诱导蕴涵，即

当φ＝*时，二元运算←*：L×L→L称为对偶诱导蕴涵，即

定义 1.6［20］设二元运算*：L × L → L，如果* 满足：∀a，bλ∈ ［0，1］，λ ∈ Λ（Λ ≠ Ø），

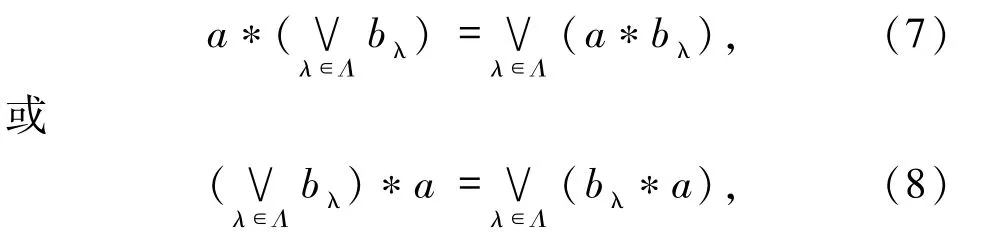
则称*是左（右）无限∨-分配的.如果*既是左无限∨-分配的，又是右无限∨-分配的，则称*是无限∨-分配的.类似地，如果*满足：

则称*是左（右）无限∧-分配的.如果*既是左无限∧-分配的，又是右无限∧-分配的，则称*是无限∧-分配的.如果*既是无限∧-分配的，又是无限∧-分配的，则称*是无限分配的.

引理 1.1［15］设*：L × L→L单调递增，则二元运算*是连续的当且仅当*是无限分配的.

引理 1.2［15］设 ｛t∈L：a*t≤b｝≠Ø，∀a，b∈L.如果单调递增的二元运算*：L×L→L关于第二变元左连续，则L上诱导蕴涵（5）式存在.

引理 1.3［15］设 ｛t∈L：a*t≤b｝≠Ø，∀a，b∈L.如果单调递增的二元运算*：L×L→L关于第二变元右连续，则L上对偶诱导蕴涵（6）式存在.

引理 1.4［19］设二元算子*：L×L→ L为单调递增运算，a，b∈L且诱导蕴涵（5）式存在，则

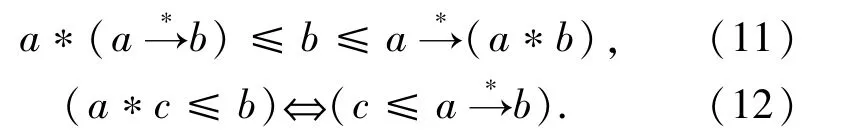
如果对偶诱导蕴涵（6）式存在，则

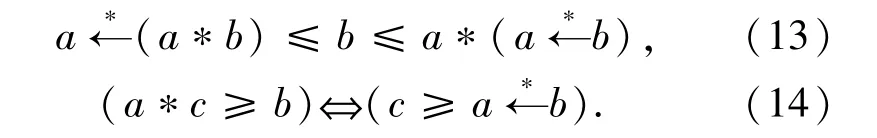
引理1.5［21］如果二元运算*是单调递增的，则max-*合成运算也是单调递增的，即

定义 1.7［22］设（P，≤）是偏序集且 Ø ≠X⊆P.如果p∈X满足x≤p，∀x∈X有p＝x，称元素p为X的一个极小元；如果g∈X满足x≤g，∀x∈X，称g为X的一个最大元.

注1.1 方程解集中的极小元称为方程的极小解，方程解集中的最大元称为方程的最大解.

2 方程A◦X＝B的解集

本节若未特别说明，则假设*∈LRC，a，b∈L.记 S（a，b，*）＝ ｛x ∈ L：a*x ＝ b｝，S ≤ （a，b，*）＝ ｛x∈L：a*x∈b｝，S≥（a，b，*）＝ ｛x∈L：a*x≥b｝，S（A，B，*）＝ ｛X：A◦X ＝ B｝，S0（A，B，*）表示方程（1）的所有极小解构成的集合，即S0（A，B，*）＝ ｛X：X为S（A，B，*）的极小元｝.对方程 a*x ＝ b，a，b，x∈L.显然方程a*x ＝ b的解集为

引理 2.1［23］设二元运算*单调递增，X，Y∈S（A，B，*）且 X ∈ Y，则［X，Y］⊆ S（A，B，*）.

引理 2.3 S≥（a，b，*）≠Ø当且仅当1∈S ≥ （a，b，*）.

证明 ⇐ 显然.

⇒ 设x∈S≥ （a，b，*），则由引理1.5知，a*1 ≥ a*x≥ b.所以1 ∈ S≥ （a，b，*）.

证明 ⇐ 显然.

⇒ 设x0∈S（a，b，*），则a*x0＝ b≤b.由（5）式知，x0≤.又由引理1.5得，b ＝ a*x0≤a*（）≤ b.所以，a*（）＝ b，即为方程的解.又因为x0≤，故为方程的最大解.

定理 2.5 如果 S（a，b，*）≠ Ø，则 S（a，b，*）＝ ［］.

证明 设x0∈S（a，b，*），由定理2.4得为方程的最大解.又a*x0＝b≥b，由（6）式知，x0≥.由引理1.5 得

例 2.1 设 x*y ＝ x·min（x，y），其中 x，y ∈［0，1］.考虑方程a*x ＝ b，其中a ＝ 0.8，b ＝ 0.64.

由（5）和（6）式知，

接下来考虑方程

其中“◦”代表max-*合成运算.记S（a，b，*）＝｛x ＝ （xj）j∈J∈Ln：a◦xT＝ b｝，S0（a，b，*）＝ ｛x：x为 S（a，b，*）的极小元.令

引理2.6 方程（17）有解当且仅当存在j0∈J使得aj0*＝b.

证明 ⇐ 显然.

⇒ 设 x ＝ （x1，x2，…，xn）T∈ S（a，b，*），则 ∨j∈J（aj*xj）＝ b.由于J为有限集，则存在j0∈ J使得aj0｝*xj0＝ b.又由引理1.5及定理2.4知，b＝aj0*xj0≤＝aj0*（）≤b.所以，＝b.

令J＝｛j∈J：aj*j＝b｝，可得如下结论.

定理 2.7 如果 S（a，b，*）≠ Ø，则 ∀j0∈J，方程（17）有极小解 x0（j0）＝ （）j∈J，其中

推论 2.1 如果S（a，b，*）≠Ø，则方程（17）的极小解个数等于 ｜J｜，其中｜｛·｝｜表示集合｜｛·｝｜的元素个数.

定理 2.8 如果 S（a，b，*）≠ Ø，则 ∀x∈S（a，b，*）存在 x0＝ （）j∈J∈ S0（a，b，*）使得x0≤ x.

证明 因为 x ＝ （xj）j∈J∈ S（a，b，*），则（aj*xj）＝ b.由于 J为有限集，则存在j0∈ J使得aj0*xj0＝ b.又由定理2.5 知xj0∈S（aj0，b，*）＝］.令

显然x0≤x.又由定理2.7知，x0＝ （）j∈J为方程的极小解.

定理 2.9 如果 S（a，b，*）≠ Ø，则 S（a，b，*）＝ ∪x0∈S0（a，b，*）［x0，x¯］，其中［x0，x¯］＝｛x∈Ln：x0≤x≤x¯｝，∀x0∈S0（a，b，*）.

另一方面，对 ∀x∈∪x0∈S0（a，b，*）［¯］，因为方程（17）的极小解个数等于｜J｜，为有限集，则存在y0∈S0（a，b，*）使得x∈ ［¯］.又由引理2.5知，b＝a◦y0≤a◦x≤a◦＝b，故a◦x＝b，即 x ∈ S（a，b，*）.因此

例 2.2 考虑方程（0.75，0.8，0.1，1）◦（x1，x2，x3，x4）T＝ 0.64，其中 * 使用例2.1 中的运算.因为＝（1，1，1，0.64）T，经检验，∈S（a，b，*）.又因为J ＝ ｛2，4｝且＝ 0.8，＝ 0.64，所以方程有 2 个极小解，分别为 x1＝ （0，0.8，0，0）T，x2＝ （0，0，0，0.64）T.因此，方程的解集为

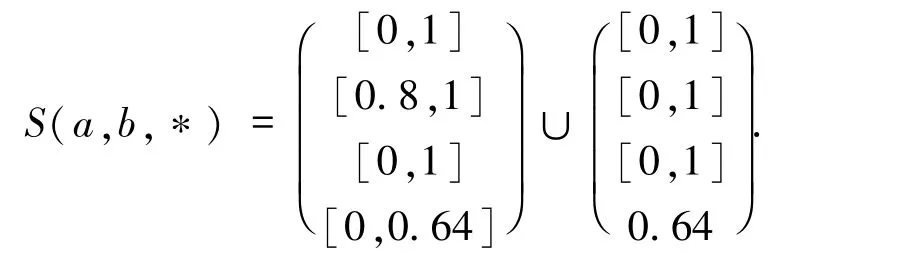
定理2.10 S（A，B，*）≠Ø当且仅当˜X是方程（1）的解.进一步，˜X为方程（1）的最大解.

证明 ⇐ 显然.

下面讨论方程（1）的极小解.

定理 2.11 设 S（A，B，*）≠ Ø，X ＝ （xj）j∈J∈ S（A，B，*），则存在 j0∈ J使得 aij0*xj0＝ bi，∀i∈ I.

定理 2.12 如果 X ∈ S（A，B，*）且 f∈J（X），则 X（f）≤ X.

定理 2.13 如果X∈S（A，B，*），则F（X）⊆S（A，B，*）.

定理 2.14 如果 X，Y ∈ S（A，B，*），X ≤ Y，X（f）∈ F（X），则 f∈ J（Y）且 X（f）＝ Y（f）∈ F（Y）.

证明 设X ＝ （xj）j∈J，Y ＝ （yj）j∈J，且X≤Y.如果 f ＝ （fi）i∈I∈ J（X），则 ∀i∈ I，bi＝ aifi*xfi≤ aifi*yfi≤bi，即aifi*yfi＝ bi.因此，fi∈Ji（Y）即 f ＝ （fi）i∈I∈ J（Y）.故 X（f）＝ Y（f）∈ F（Y）.

设P是任意一个偏序集，记P的所有极小元构成集合P0.

引理2.15［24］设P为一个偏序集且Ø≠Q⊆P.如果对∀p∈P，∃q∈Q，使得q≤p，则P0＝ Q0.

引理 2.16 方程（1）的解集 S（A，B，*）与有限偏序集F（˜X）有相同的极小解集.即S0（A，B，*）＝F（˜X）0.

证明 由定理2.13知，F（˜X）⊆S（A，B，*）.若S（A，B，*）＝Ø，则S0（A，B，*）＝F（˜X）0＝Ø.若S（A，B，*）≠Ø，设X∈S（A，B，*），则由定理2.10知，X≤˜X.由定理2.14及X（f）∈F（X）可得X（f）＝˜X（f）∈F（˜X）.又由定理2.12知，X（f）≤X.所以，由引理2.15知，S0（A，B，*）＝F（˜X）0≠Ø.因此S0（A，B，*）＝F（˜X）0.

定理 2.17 如果S（A，B，*）≠Ø，则S（A，B，*）＝［X0，X˜］，其中［X0，X˜］＝ ｛X∈Ln：X0≤X≤X˜，∀A0∈F（X˜）0.

证明 设 X ∈ S（A，B，*），由定理2.16 的证明知，存在Y∈F（X˜）使得Y≤X.又因为F（X˜）为有限集，则存在X0∈F（X˜）0使得X0≤Y.所以，X0≤Y≤X≤X˜，即X∈ ［X0，X˜］.因此，S（A，B，*）⊆［X0，X˜］⊆S（A，B，*）.所以，S（A，B，*）＝［X0，X˜］.另一方面，由引理1.5及定理2.13知［X0，X˜］⊆S（A，B，*）.所以，S（A，B，*）＝［X0，X˜］.

定理2.18 方程（1）有唯一解当且仅当F（˜X）＝｛˜X｝.

证明 ⇐ 由定理2.10与定理2.13可证得.

⇒ 由定理2.17可证得.

下面给出求解方程（1）极小解的步骤.

第1步：根据定理2.10计算˜X并检验˜X是否为方程（1）的解.如果不是，则 S（A，B，*）＝ Ø，结束；否则，转至第2步；

第2步：根据（19）式构造Ji（˜X），进一步，由（20）式构造J（˜X）；

第3步：根据（22）式构造F（˜X）；

第4步：根据定理2.16求出方程的极小解S0（A，B，*）＝F（˜X）0；

第5 步：输出 S0（A，B，*）.

例 2.3 考虑方程（1），其中

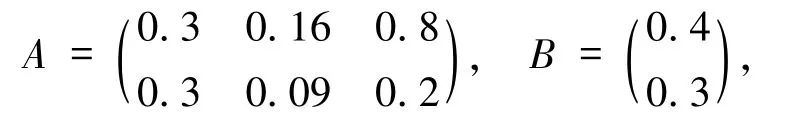
经计算，˜X＝［0.3，1，0.2］T.经检验，˜X是方程的解，由（19）式得 J1＝ ｛2，3｝，J2＝ ｛1，2｝，则J（˜X）＝｛（2，1），（2，2），（3，1），（3，2）｝.

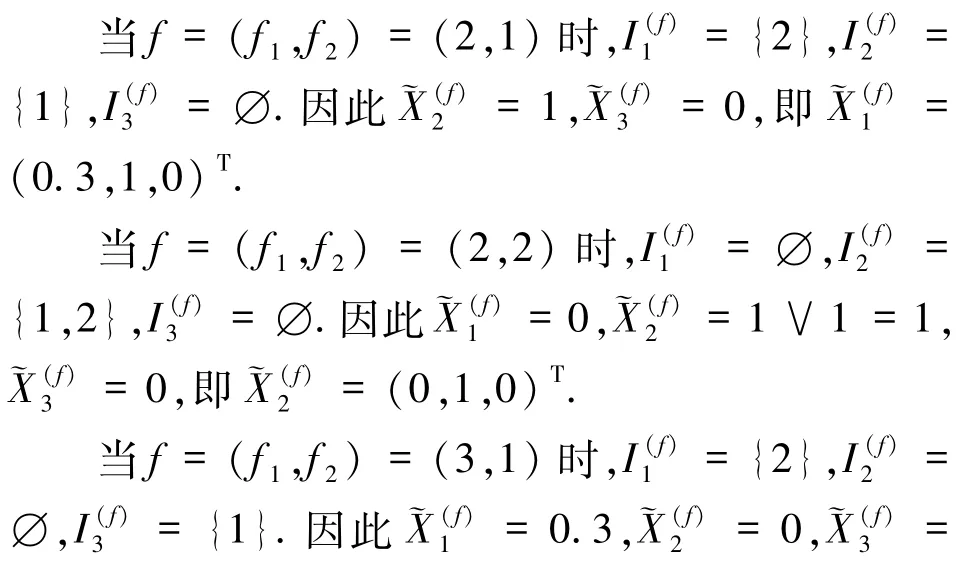
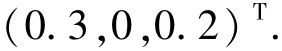
当f＝ （f1，f2）＝ （3，2）时｛2｝，＝ ｛1｝.因此0.2，即＝ （0，1，0.2）T.

*使用例2.1中的运算，则˜X＝（0.8，0.75，0.5，0.6）T.经检验，˜X是方程的解，由（19）式得J1＝｛1｝，J2＝｛2，4｝，J3＝｛3｝，J4＝｛3｝，则J（˜X）＝｛（1，2，3，3），（1，4，3，3）｝.