非线性耦合Klein-Gordon方程组的精确行波解与分支

汪春江， 舒 级， 李 倩， 王云肖， 杨 袁

（四川师范大学数学与软件科学学院，四川成都610066）

一直以来，非线性现象都是基础数学和应用数学关注的主题，对于非线性演化方程的精确解研究在数学物理上有着重大作用，常系数方程［1-3］、变系数方程［4-5］、随机方程［6-7］的精确解已经被广泛研究，并给出了很多研究精确解的方法，如逆散映射法［8-9］、Backlünd 变换［10-11］、达布变换［12］、齐次平衡法［13］、（G′／G）- 展开法［14］等.

本文考虑带有标量场ν的非线性耦合Klein-Gordon方程组

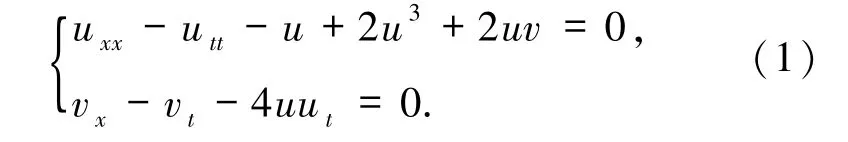
解方程组（1）有很多方法，例如，双曲正切法［15］、首次积分法［16］等.应用这些方法可以得到许多类型的精确解.在这里，将应用动力系统方法来获得方程组（1）的行波解的分支与相图.

本文运用动力系统的分支理论，在相平面（φ，y）中得到了行波系统的所有分支与相图，而且所有精确行波解与方程组（1）的相图轨道相关.与此同时，可以发现方程组（1）有孤立波解、周期波解［17］，而且所有行波解都是参数表示形式.在物理上，这2类解有不同的意义，其中孤立波解表示方程的波函数在运动过程中只有一个波峰或波谷，而周期波解则表示波函数以某个周期在运动.

1 行波系统

首先作行波变换：

u（x，t）＝ φ（ξ）， v（x，t）＝ ψ（ξ）， ξ＝ （x-λt），其中，λ2≠1.将行波变量 ξ＝x-λt代入方程组（1），得到

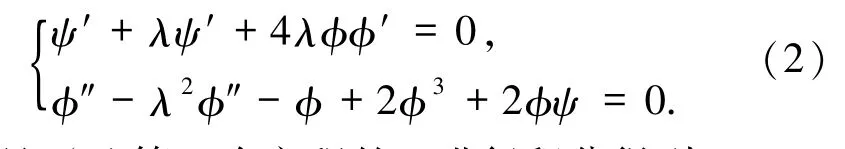
对方程组（2）第一个方程的ξ进行积分得到

其中，c1是积分常数.

将方程（3）代入到方程组（2）第一个方程得到

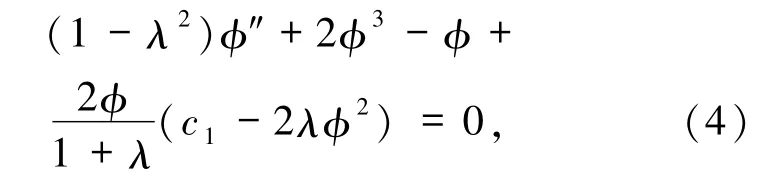
于是方程组（2）等价于平面可积系统

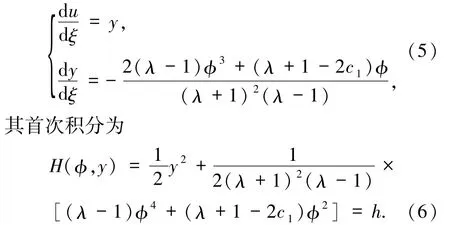
假设 u（x，t）＝φ（ξ）是方程组（1）在（-∞，+∞）上的连续解，并且

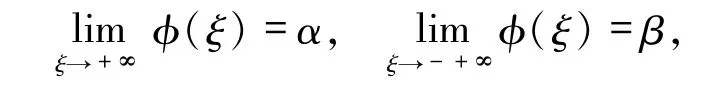
则下面2个结论是众所周知的：

（i）当 α ＝ β 时，称 u（ξ）是孤立波解；

（ii）当 α≠β 时，称 u（ξ）是扭波解.

一般来说，方程组（1）的一个孤立波解对应着方程组（5）的同宿轨道；方程组（1）的一个扭波解对应着方程组（5）的异宿轨道；方程组（1）的一个周期波解对应着方程组（5）的周期轨道.因此，为了考察方程组（1）的孤立波和扭波的所有分支，就必须找出Hamilton系统（5）在参数空间（λ，c1）下对应的周期环、同宿和异宿轨道.在我们的研究中，平面动力系统的分支理论［18-21］起着重要的作用.

2 Klein-Gordon方程组的分支与相图

下面研究平面Hamilton系统（5）的分支集和相图.显然，在（φ，y）-平面上，系统（5）的平衡点的横坐标是函数

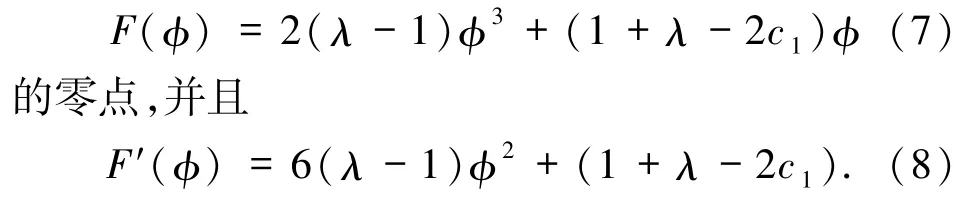
若（φi，0）是系统（5）的平衡点，则在这一点处系统（5）所决定的Jacobi行列式为

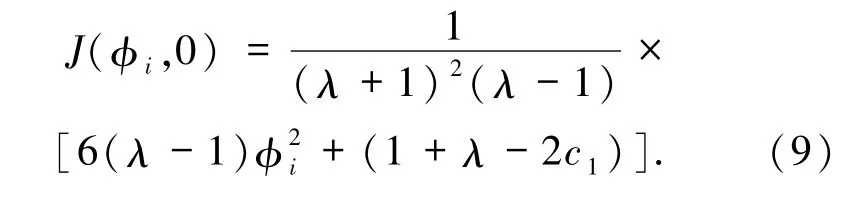
根据平面动力系统的分支理论，如果J（φi，0）＜0，称这个平衡点为鞍点；如果 J（φi，0）＞0 且Trace（M（φi，0））＝0，称这个平衡点为中心点；如果J（φi，0）＞0 且（Trace（M（φi，0）））2-4J（φi，0）＞0，称这个平衡点为结点；如果 J（φi，0）＝0且这个平衡点的 Poincaré指数为 0，称这个平衡点为尖点［22］.

接下来，对参数λ、c1的不同情况进行讨论.

情形 1 c1＞1.

a）当 λ∈（1，2c1-1）时，有3 个平衡点：

把这3个根分别带入（9）式的线性化系统的行列式，得到：

图1 当 c 1＞1，λ∈（1，2c 1-1）时，系统（5）的相图Fig.1 When c 1＞1，λ∈（1，2c 1-1），phase portraits of the system （5）

b）当λ∈（-∞，1）∪［2c1-1，+∞）时，有1个平衡点φ1＝0，把这个根带入系统（5）的线性化系统的行列式，得到

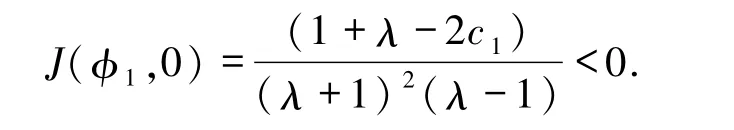
此时，系统（5）有 1 个鞍点（0，0）.在点（0，0）周围存在无数个周期轨道.这表明方程组（1）有无数个周期解，见图2.

情形 2 c1＜1.

图2 当 c 1＞1，λ∈（-∞，1）∪［2c 1-1，＋∞）时，系统（5）的相图Fig.2 When c 1＞1，λ∈（-∞，1）∪［2c 1-1，＋∞），phase portraits of the system （5）

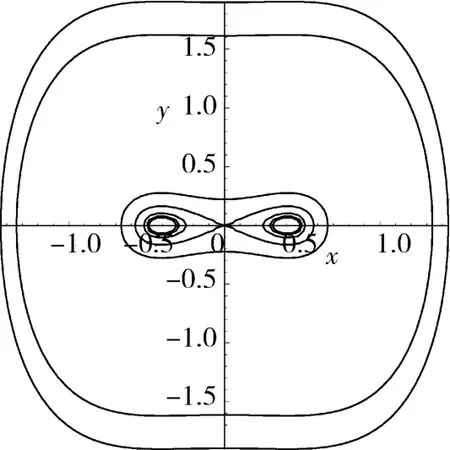
图3 当 c 1＜1，λ∈（2c 1-1，1）时，系统（5）的相图Fig.3 When c 1＜1，λ∈（2c 1-1，1），phase portraits of the system （5）

b）当 λ∈（-∞，2c1-1］∪（1，+∞）时，有1个平衡点φ1＝0，把这个根分别带入系统（5）的线性化系统的行列式，得到

此时，系统（5）有 1 个鞍点（0，0）.在点（0，0）周围存在无数个周期轨道.这表明方程组（1）有无数个周期解，见图4.

图4 当 c 1＜1，λ∈（-∞，2c 1-1］∪（1，＋∞）时，系统（5）的相图Fig.4 When c 1＜1，λ∈（-∞，2c 1-1］∪（1，＋∞），phase portraits of the system （5）

3 Klein-Gordon方程组的所有行波解

由于上述情形2的精确解与情形1类似，只讨论情形1的情况.通过系统（5）与Hamilton函数的计算，得到了下列结果.

情形 1 c1＞1，λ∈（1，2c1-1）.

（i）根据 H1（φ，y）＝h，h∈（h3，0）所定义的系统（5）的2簇周期轨道，可得到

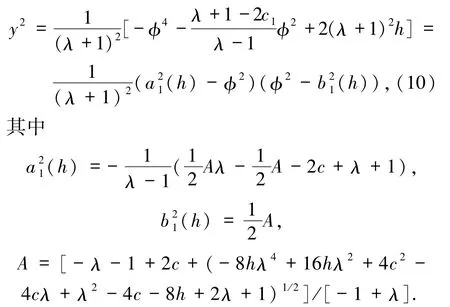
从而得到周期轨道的参数表达式

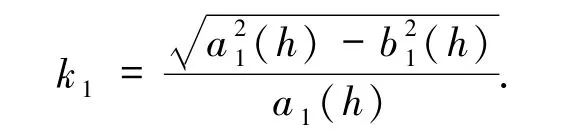
（ii）根据 H1（φ，y）＝h，h＝0 所定义的系统（5）的2个同宿轨道，可得到参数表达式

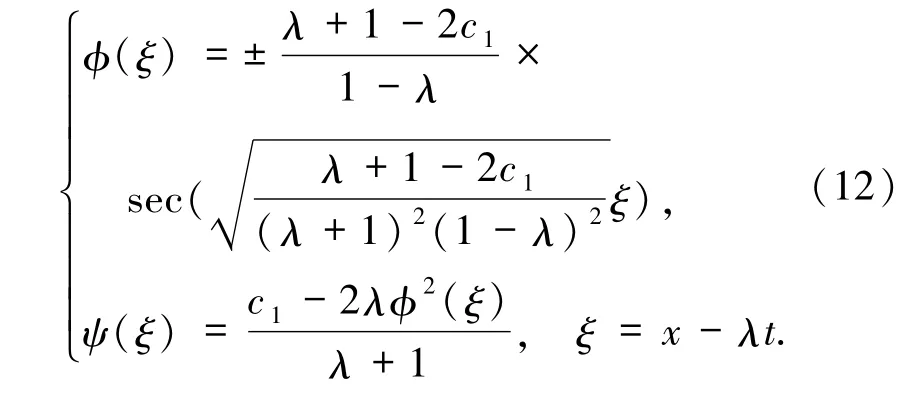
（iii）根据 H1（φ，y）＝ h，h∈（0，∞）所定义的系统（5）的周期轨道，得到

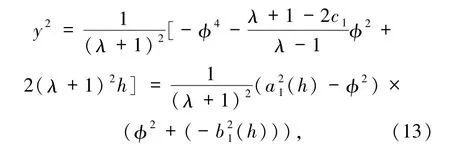
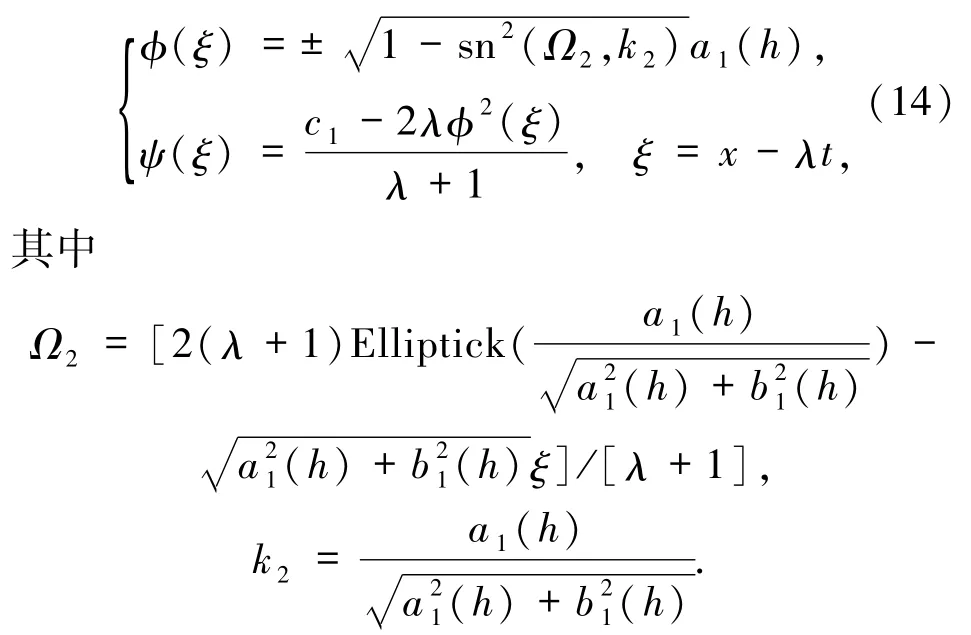
情形 2 c1＞1，λ∈（-∞，1）∪［2c1-1，+∞）.

根据 H1（φ，y）＝h，h∈（0，∞）所定义的系统（5）的周期轨道（包含了平衡点（0，0）），有

从而得到参数表达式

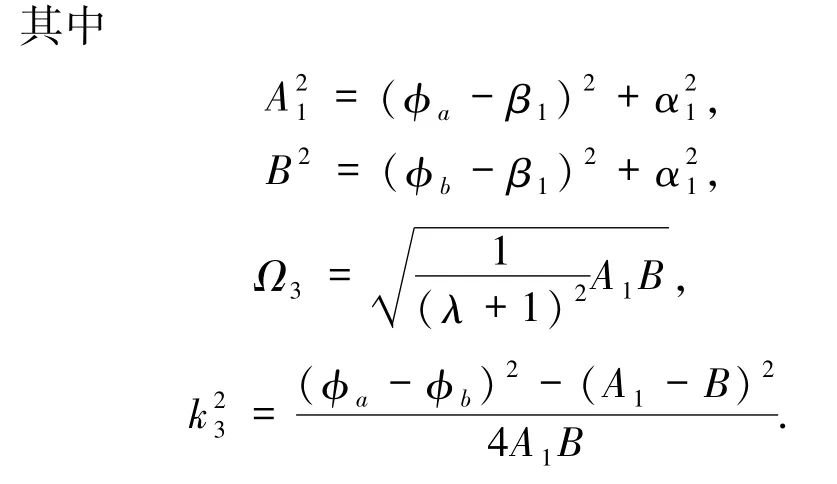
下面的图5～8为精确解（12）在参数c、λ取不同值下的行波解图.

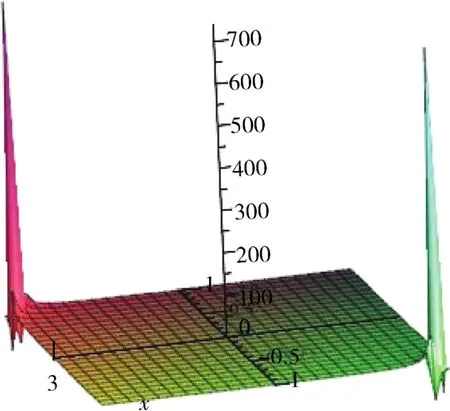
图5 当 c 1＝2，λ＝2时，精确解（12）的 φ（ξ）Fig.5 When c 1＝2，λ＝2，φ（ξ）of exact solution（12）

图6 当 c 1＝2，λ＝2时，精确解（12）的 ψ（ξ）Fig.6 When c 1＝2，λ＝2，ψ（ξ）of exact solution （12）

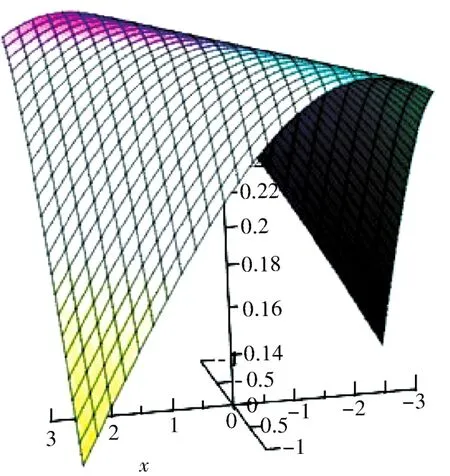
图7 当 c 1＝ -1，λ＝ -2时，精确解（12）的 φ（ξ）Fig.7 When c 1＝ -1，λ＝ -2，φ（ξ）of exact solution （12）

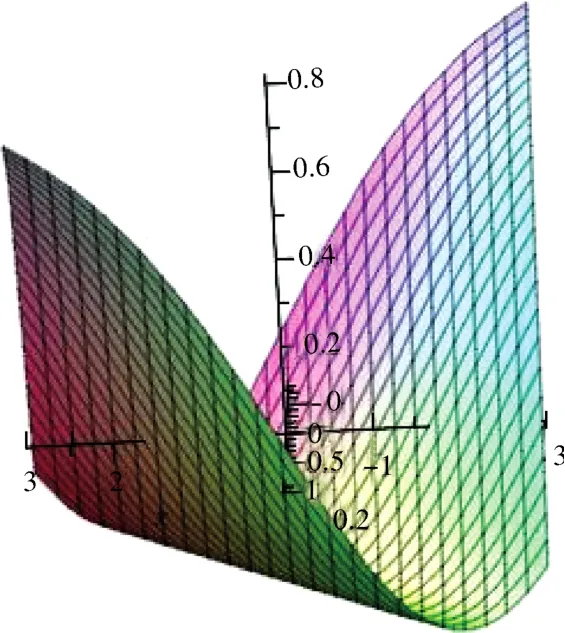
图8 当 c 1＝ -1，λ＝ -2时，精确解（12）的 ψ（ξ）Fig.8 When c 1＝ -1，λ＝ -2，ψ（ξ）of exact solution （12）

4 结论

本文在诸多学者和专家研究的基础上，运用平面动力系统分支理论得到了关于参数c1、λ在不同取值下，耦合非线性 Klein-Gordon方程组的行波解的分支与相图，并利用这些分支、相图进一步得到所研究方程的2种形式的精确行波解，包括孤立波解和周期波解.这些结果可能对研究更加复杂的物理现象有一定的帮助.下一步，将利用平面动力系统分支理论对非线性演化方程组中方程的条件以及方程的个数做深一步的研究.