2维和4维时空温度弦模型中暗能量玻色子星质量和物态参量的计算

钟 鑫， 颜 骏， 余 毅

（四川师范大学物理与电子工程学院，四川成都610066）

20世纪80年代以来，超弦理论研究已取得了很大的进展.理论物理学家广泛研究了弦的紧致化、弦的量子化、弦与共形场论以及可解的2维量子引力模型的深刻联系等一系列问题.这些研究极大地丰富了人们对高能标下微观世界的认识，但是人们对高温状态下的弦模型的物理内涵却了解得较少，而现实的弦模型总是希望考虑温度的影响，如在甚早宇宙中和致密星体内部，温度是一个至关重要的物理因素.另一方面，Ia型超新星和宇宙微波背景辐射的观测表明宇宙在加速膨胀，而暗能量被认为是加速膨胀的可能推动因素［1-6］.2004年，英、美天文学家将“钱德拉”望远镜和美宇航局“威尔金森微波各向异性探测器”的观测结果结合起来，对宇宙的物质构成比例给出了新的估计，宇宙中暗能量占75%左右，暗物质为21%，剩下4%是可见物质.由于目前黑洞的事件视界没有直接的观测证据，人们猜测星体还可能形成新的演化形态，如暗能量星或引力真空星［7-13］.近年来对孤子的研究已经深入到天体物理领域，文献［14-15］基于粒子物理中的非拓扑孤子首先提出了存在一种冷的、稳定的、大量的相干态星体—孤子星.

文献［16-17］用几何方法直接计算了黎曼面上的自由能，发现了一个独特的现象，即弦的自由度远小于通常量子场论中的自由度的数目，在这一结论的基础上猜想拓扑量子场论可能正对应于弦的末破缺相.另外，由于暗能量可能对星体的平衡产生影响，其负压强产生的等效斥力作用，阻止了星体进一步的引力塌缩，就可能形成各种不同形式的暗能量星，目前天文观测数据支持这类暗能量星的形成［18］.本文将根据温度弦理论研究一种新的暗能量玻色子星模型.

1 高亏格黎曼面上玻色弦自由能的计算

首先讨论玻色弦气体自由能的计算，考虑作用弦的多圈费曼图时，需要计算高亏格黎曼面上的路径积分.在亏格g黎曼面上选一组典范同基调基ai、bi，i＝1，2，…，g，如图1 所示，其相交数定义［19-22］为

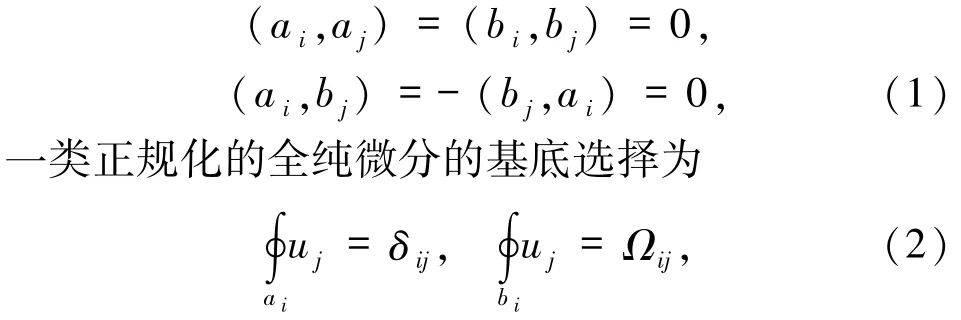
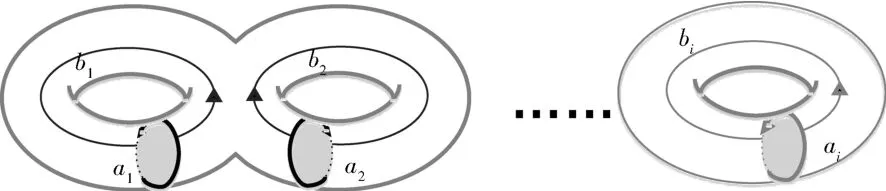
图1 亏格g黎曼面的几何拓扑图形Fig.1 Geometric topology graph of genus g Riemann surface

接下来通过时间坐标X0环半径2π／β的紧致化的引入温度参量，令

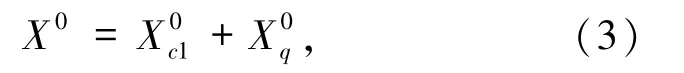
沿着ai的边界条件为+ βni，沿着 bj的边界条件为+ βmj，这里 ni、mj是绕数.由于＝0，所以还可表示为

以及正规化条件（2）式可得

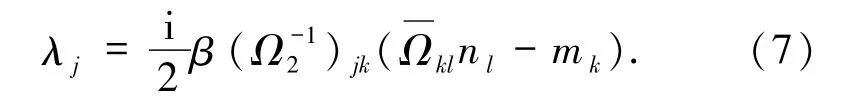
将（3）和（4）式代入到原始作用量中得到量子和经典两部分

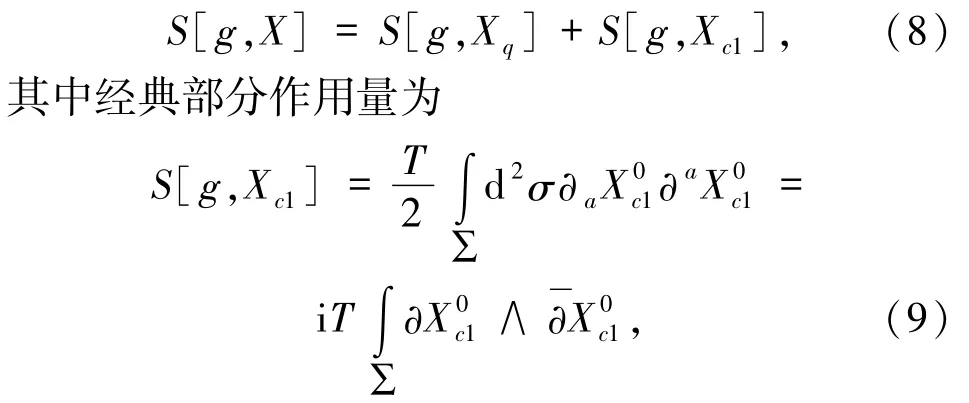
T是弦张力，再利用如下双线性黎曼关系

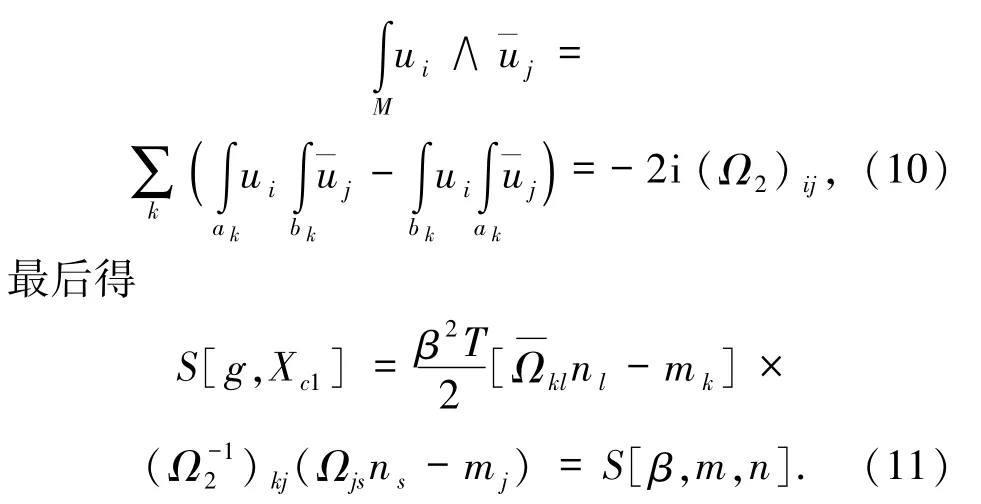
对 Xu（σ）、gab（σ）路径积分得自由能

锁销检测：MCU进行相应检测。优势：功耗低，通信方便快捷。劣势：是否这样就无法实现用手持机对其进行读写了？

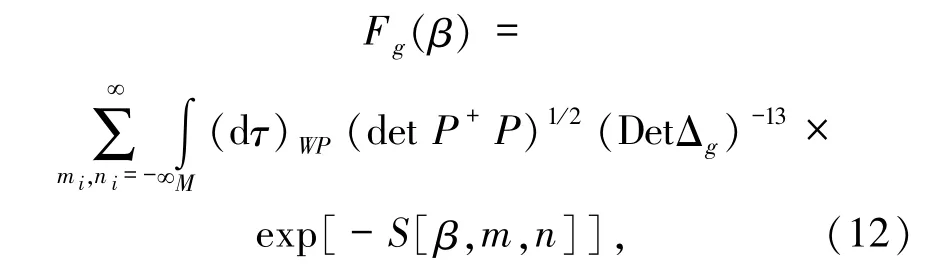
其中，P+P是微分算子

这里对绕数的求和为

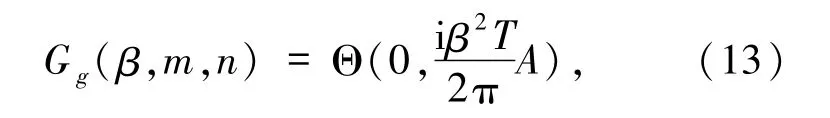
其中黎曼Θ函数定义为

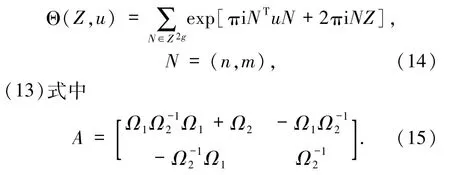
由此可以推导出弦作用的多圈自由能，（13）式中的Sg（β）可表示为

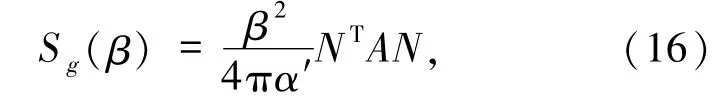
其中，NT＝ （ni，mj）代表绕数矩阵，经过路径积分后得到亏格g黎曼面上的玻色弦自由能为

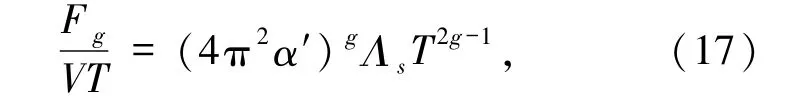
其中，V 是体积，Λs＝ ε2（g-1）Λg，Λg是 g 圈宇宙常数，ε是弦耦合常数.能量密度和压强分别由下述公式计算

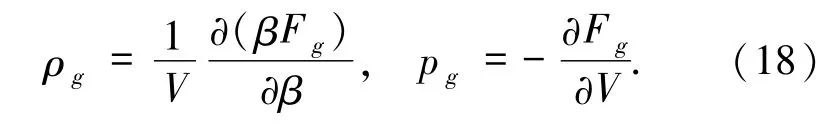
由（17）式可知，玻色弦自由能和温度的幂形式有关，当g＝1，单圈自由能F弦～T2，而通常量子场论计算出的玻色子自由能为F场～T4，所以F弦≪F场.将（17）式代入（18）式可以算出能量密度和压强的具体表达式，这时弦理论和量子场论算出的这些热力学量的数量级有较大差别.

2 D＝2维时空暗能量玻色子星的质量和物态参量

为了研究暗能量星的质量和物态参量，弦修正的引力作用量［23］选择为

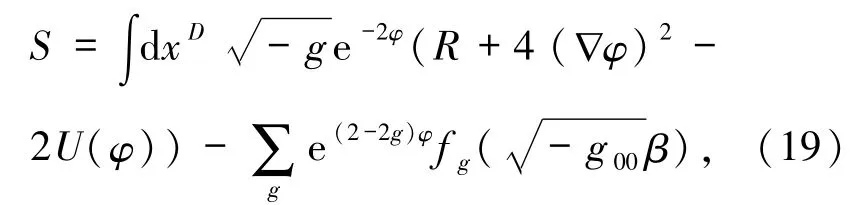
其中，D是时空维数，g是度规行列式，R是标量曲率，φ是dilaton场，U（φ）是势能，fg是单位体积自由能，作用量（19）式对应的引力场方程和dilaton场方程分别为

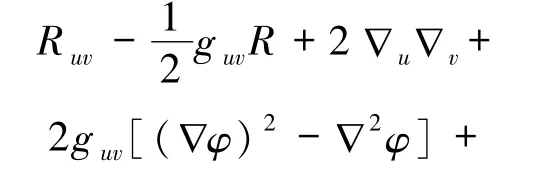
其中，度规因子α为坐标x的函数，由此度规可导出如下的克氏联络

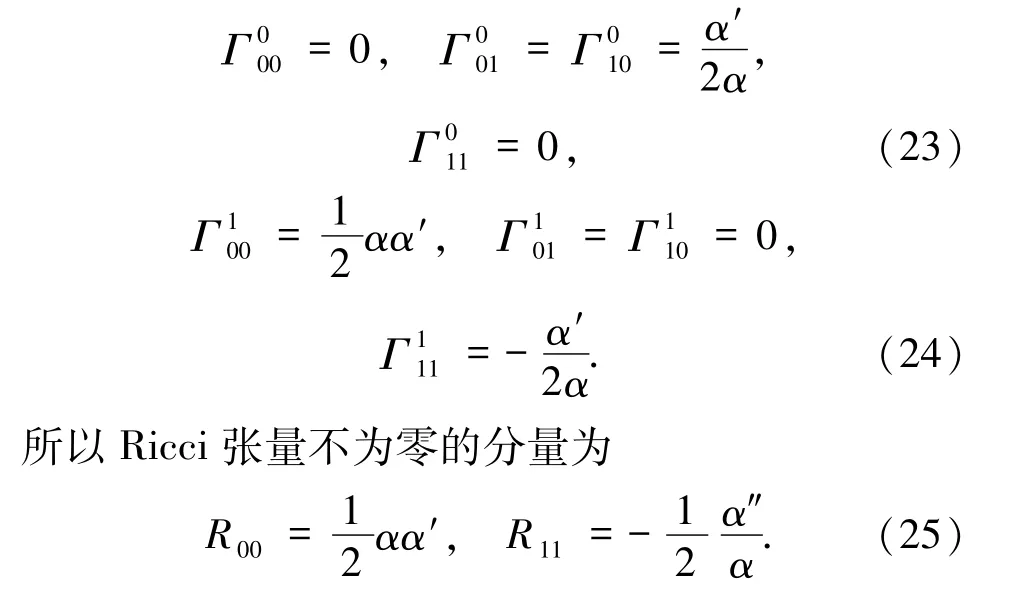
另外，标量曲率为R＝-α″.经过详细计算后发现Einstein张量为

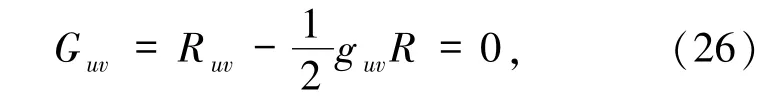
这是2维引力模型中的一个重要特点.利用这一性质可以简化引力场方程，降低求解方程的难度.暗能量dilaton场的协变导数分别为：

经过仔细推导得到引力场的2个分量方程

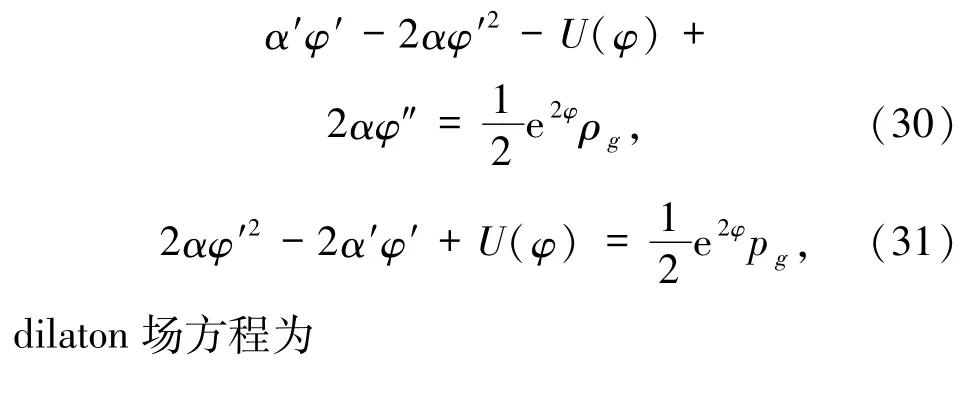
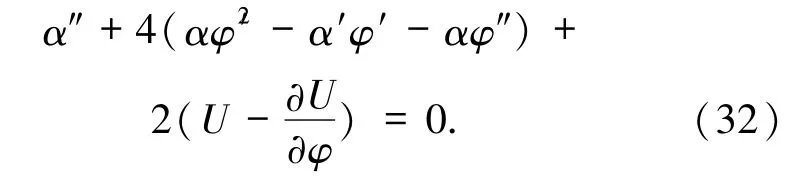
由方程（30）和（31）式可定义如下有效能量密度和压强

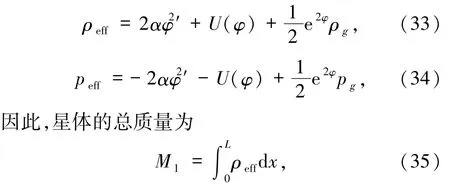
这里，L是星体尺度大小，物态参量定义为

将弦理论或量子场论计算出的热力学量的具体表达（18）式代入引力场方程（30）和（31），并利用dilaton场方程（32），通过设定度规 α、dilaton场 φ和势能U（φ），以及温度T和坐标x的具体关系式，那么可以求出这些物理量的解析解，并进一步计算出星体的质量M1和物态参量w1的具体数值.

3 D＝4维时空暗能量玻色子星的质量和物态参量

（3+1）维时空中的定态度规为

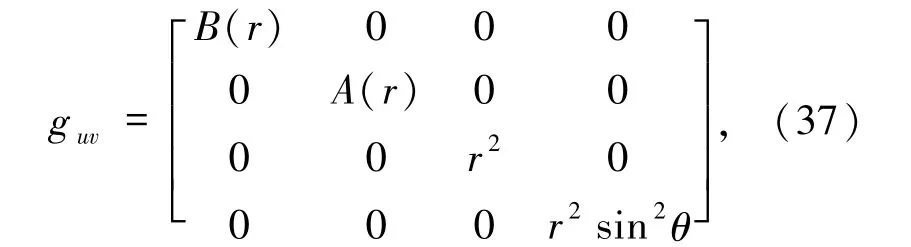
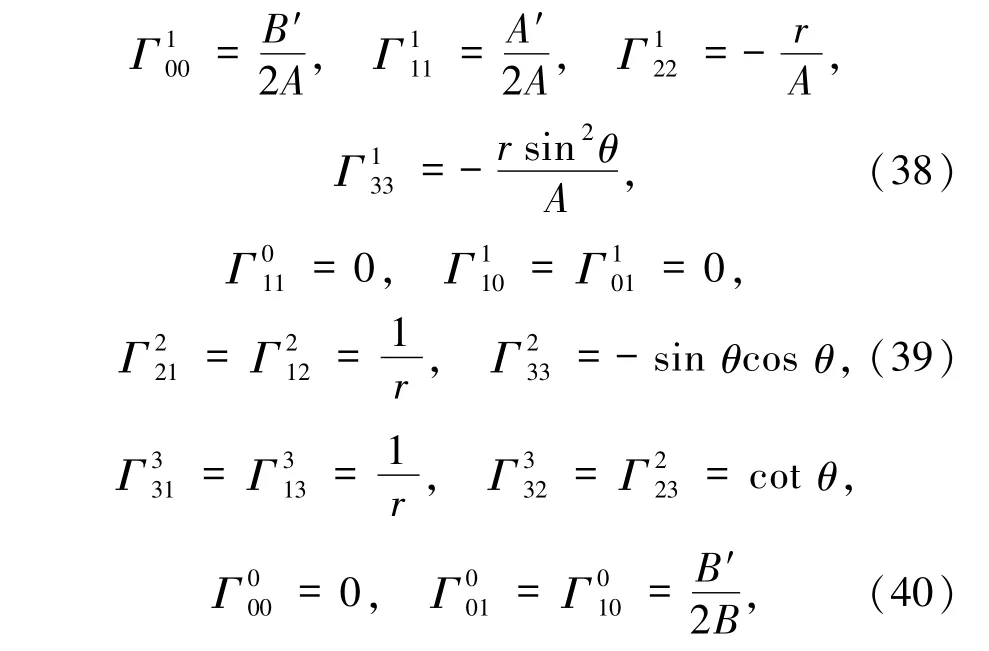
所以Ricci张量不为零时，分量分别为：

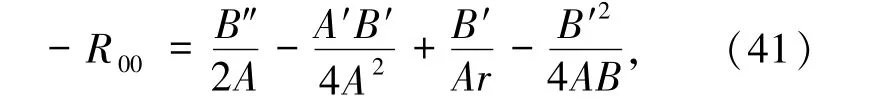
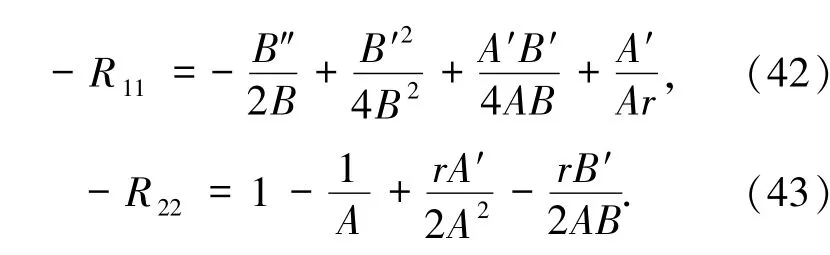
另外，R33＝ sin2θR22，标量曲率为 R ＝ guvRuv，Einstein张量Guv≠0，根据度规和Ricci张量可以推导出这2个几何量.另外，玻色弦流体物质的能量动量张量分别为：

这时引力场方程的2个分量方程变为：

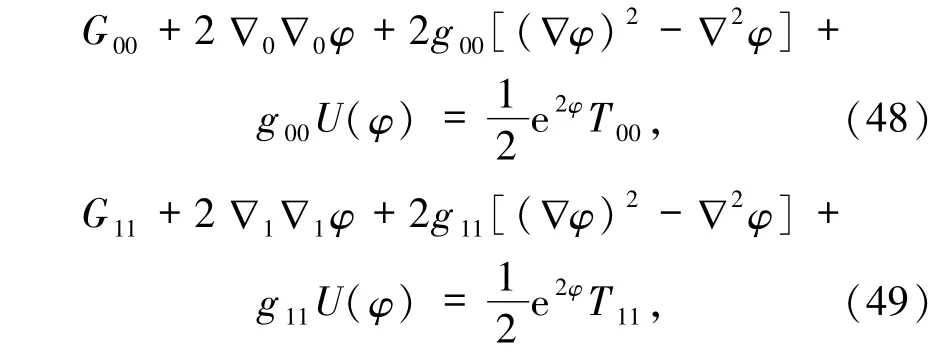
dilaton标量场方程为

这里V是体积元，R是星体半径，物态参量定义为

将Ricci张量（41）～（43）式和dilaton场的协变导数（45）～（47）式代入（48）、（49）式和（50）式后，便可得到引力场方程和dilaton场方程的具体形式，不同于2维时空中的场方程，这些4维场方程无法通过设定物理量和坐标r的关系式来求出解析解，通常都通过数值解的方法来计算星体质量和物态参量的具体数值，这也是2维引力和4维引力理论的一个主要区别.

4 讨论

本文根据温度弦模型分别推导了2维和4维暗能量玻色子星的质量和物态参量的表达式，研究结果表明不同时空上的计算结果有一定差别.首先，2维引力中的联络分量和Ricci张量以及协变导数都比4维引力中对应的物理量简单；其次，2维引力中Einstein张量Guv＝0，这一性质可以简化引力场方程，4维引力中Guv≠0，因此场方程比较复杂；通常2维引力场方程和dilaton场方程可以通过设定物理量和坐标的关系求出解析解，而4维引力场方程只能通过数值方程求解.所以，2维引力模型中星体的质量和态参量可以计算出解析表达式，这有助于具体分析星体的内部结构和物理性质，为4维星体的物理研究提供一个理论的实验室.当星体中弦气体的能量密度和压强均大于零，因此其物态参量v为正值，如果总能量密度ρeff为正值，总压强peff为正值，这时星体处于正常玻色子星状态，如果总压强peff为负值，那么dilaton场表现为暗能量，则星体处于暗能量玻色子星状态.

另外，由于弦理论和量子场论计算出的自由能有T2数量级的差别，所以对应的能量密度和压强有所不同，因此通过这两种理论计算出的星体质量和物态参量也有区别，比较这些不同理论得出的暗能量玻色子星的计算结果，无论对于理论研究还是进一步的天文观测，都是非常有意义的研究课题.