高中数学新授课中“问题导入”的若干探究

□王志刚

（西安交大阳光中学，陕西西安 710043）

苏霍姆林斯基说：“如果老师不想办法使学生产生情绪高昂的智力振奋的内心状态，就急于传授知识，那么这种知识只能使人产生冷漠的态度，而给不动感情的脑力劳动带来疲劳.”所以精彩而成功的课堂导入，一方面能提高学生的学习兴趣，调适教学的气氛，诱发学生的思维，激起学生学习的求知欲，另一方面也能有效地消除其他课程的延续思维，将学生课前分散的注意力迅速转移到课堂上，使学生很快进入新课学习的最佳心理状态，提高课堂学习效率.因此能否让学生迅速处于积极的状态，及时进入课堂，是有效课堂的首要问题.那么新授课的“问题导入”怎么处理？本文基于新授课的教学实践，谈谈如何开展课堂导入.

一、新授课导入应激发学生的探求兴趣

“兴趣是最好的老师”，高中数学内容相对比较抽象，课堂提问可以创设情境，使枯燥的数学知识活跃起来，以激发学生的学习兴趣，引导学生主动参与数学学习.

例1《等差数列前n项和》的导入：泰姬陵坐落于印度古都阿格，是17世纪莫卧儿帝国皇帝沙杰罕为纪念其爱妃所建，它宏伟壮观，纯白大理石砌建而成的主体建筑叫人心醉神迷，成为世界七大奇迹之一.陵寝以宝石镶饰，图案之细致令人叫绝.传说陵寝中有一个三角形图案，以相同大小的圆宝石镶饰而成，共有100层（见图1），奢靡之程度，可见一斑.你知道这个图案一共花了多少宝石吗？

图1

【设计意图】这导入源于历史，富有人文气息.图中算数，形象直观，启迪思路，能够激发学生的兴趣.因此，教师备课时应根据教材内容及学生的认知水平，选择现实生活中人们比较感兴趣的事例，构建相关的趣味性问题，吸引学生，调动学生学习数学的积极性，提升课堂教学效率.

二、新授课导入应符合数学的特点

数学的特点是严谨、逻辑性较强.在新授课的探究中，新课的导入可以为本节课创造条件，体现数学的严谨性.这样设计导入部分，能够使课堂层层递进，步步为营，能使学生在循序渐进中不断提高数学的能力，培养学生的数学品质.

例2《等差数列前n项和》的导入：如图2，一个堆放小球的V形架的最下面一层放一个小球，往上每一层都比它下面一层多放一个，最上面一层放100个.这个V形架上共放着多少个小球？

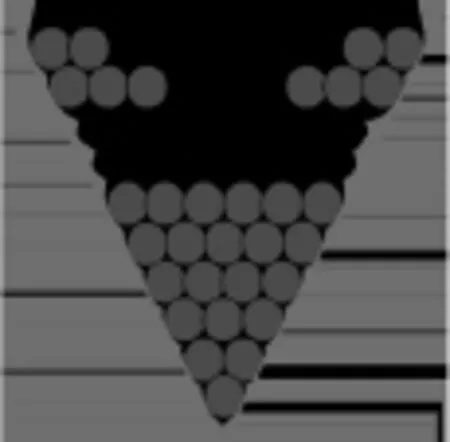
图2

问题就是：1+2+3+4+…+100=？

该问题就是等差数列的求和问题，我们这节课就来讨论等差数列的前n项和.

【设计意图】以问题导入，调动学生的积极性，目的是引入：1+2+3+4+…+100=？这样导入有两个目的：（1）为研究高斯的求和做准备，有一种顺理成章、水到渠成的感觉；（2）为高斯求和的“倒序相加”做好数形结合做铺垫.因为在处理等差数列前n项时，“倒序相加”的“形”的思想很重要，这样可以培养学生数形结合的思想，另一方面更容易理解“倒序”的原理（见例3）.

例3思考：我们换角度分析，如何用图形来说明这种算法思想？（见图3）

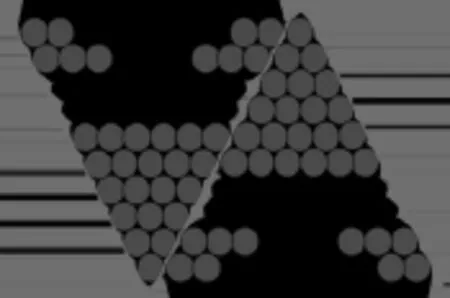
图3

【设计意图】借助几何图形的直观性，引导学生使用熟悉的几何方法：把“全等三角形”倒置，与原图补成平行四边形，这样引导学生实现由图形的倒置拼补迁移到数式求和的倒序相加，从而突破本节课的难点.让学生从计算验证到及时对倒序相加的应用范围做理性归纳，促进学生的思维向深度发展，培养严谨的数学品质.

三、新授课导入可以数学文化渗透

数学的内涵，包括用数学的观点观察现实，构造数学模型，学习数学的语言、图表、符号表示，进行数学交流.通过数学文化的引导和渗透，能够培养严谨素质，追求创新精神，欣赏数学之美.

例4《等差数列前n项和》的导入：《张邱建算经》中“分钱问题”为：今有与人钱，初一人与三钱，次一人与四钱，次一人与五钱，以次与之，转多一钱.问钱几何？

意思是说：将钱分给若干人，第一人给3钱，第二人给4钱，第三人给5钱，以此类推，每人比前一人多给1钱，问总共有多少钱？

【设计意图】以数学史《张邱建算经》为背景，一方面是渗透数学文化，为数学教学输入新鲜血液.另一方面，通过数学文化的渗透，可以提高学生的学习积极性，提高学习兴趣.

课堂中融入数学文化，很多教师只是把数学史的问题简单摆设出来，解决一个数学史的数学问题，这样是不合理的.当然，数学文化离不开数学史，但是不能仅限于数学史.正如新课改的要求，在教学中要渗透数学文化，渗透到课堂的导入、渗透到课堂的问题、渗透到数学知识的解决.当数学文化的魅力真正渗入教材、到达课堂、融入教学时，数学就会更加平易近人，数学教学就会通过文化层面让学生进一步理解数学、喜欢数学、热爱数学.

四、新授课导入可以复习引入

复习导入的教学方法是数学新授课常见的方法，该方法能起到承上启下、温故知新的作用.它是利用数学新旧知识之间的联系导入新课，也便于教师循序渐进地开展教学，也能有效降低学生对新知识的认知难度.复习导入法符合学生学习知识由浅入深、循序渐进的认识规律.这种课堂导入法，要求教师在备课时要认真研究新、旧课之间知识的内在联系，可以以问题的形式复习，这样一个或几个问题可以激发学生的思考的欲望，从而为新课做好最佳的准备[1].

例5《余弦定理》新授课的导入：复习：（1）正弦定理的内容是什么？（2）正弦定理的使用范围是什么？思考：已知三角形的两边a，b和其夹角C，能否用正弦定理解决？

【设计意图】在复习回顾时，学生回忆正弦定理和正弦定理的适用范围，提出问题引导学生思考正弦定理并不全能，从而引进余弦定理.这样导入，学生能从旧知识的复习中发现一串新知识，清楚理解余弦定理使用什么类型的三角形，并为余弦定理的应用做好了铺垫.

五、新授课导入可以类比导入

类比导入法也是数学新授课的导入法之一，即以已知的数学知识类比未知的数学新知识，以简单的数学现象类比复杂的数学现象，使抽象的问题形象化，引起学生丰富的联想，调动学生的非智力因素，激发学生的思维活动.

例6《等比数列》的导入：如果一个数列从第二项起，每一项与它前面一项的差都等于同一个常数，这样的数列称为等差数列.问：把“差”改成“比”呢？

【设计意图】以类比的形式让学生通过等差数列的概念，联想并领会等比数列的概念，通过这样的问题导入，学生可以从本质上理解等差和等比数列的区别.这样的导入，也引导学生比较未知的等比数列与已知的等差数列的各个侧面，揭示教学的重点和难点，对前后联系密切的知识教学具有温故知新的特殊作用.

六、新授课导入应寻找最近发展区

新授课问题导入，教师首先要研读教材，针对学生的认知水平和思维能力，找到问题的切入口.课堂提问应着眼于学生的“最近发展区”，若问题过易，则无法调动学生的积极性，浪费有限的课堂时间；若问题太难，学生回答不了而失去信心，使提问失去价值，要在“已知区”与“最近发展区”的结合点上设问，使学生“蹦一蹦，摘得到”，从而将学生的思维逐步引向深入.

例7《组合》的导入：引例：（1）从2，3，4，5中任取两个数相除；（2）从2，3，4，5中任取两个数相乘.问：两个问题中哪一个是排列？（1）和（2）有何不同特点？

【设计意图】以“引例”的形式给出问题，一方面利用“最近发展区”（上节课的排列知识）激发学生的思考.另一方面引导学生明辨（1）和（2）的区别，是为组合的概念做铺垫，也是为了启发学生理解排列和组合的区别.这个导入比较直接，导入的问题（1）是排列的知识，对学生来说属于“已知区”与“最近发展区”，所以学生能够轻松“摸得着”.但问题（2）有一定难度，需要学生“蹦一蹦”.这时需要教师的恰当引导，从而为解释排列和组合的本质区别做好铺垫，也为突破本节课的难点提供了“方案”.

总之，新授课的“问题导入”方法很多，其导入的目的是要充分调动学生的内在积极因素，激发学习数学的学习欲望，教师在备课的过程中，要认真研读教材，针对学生的认知水平和思维能力，找到问题的切入口，让新授课的导入使学生处于精神振奋状态，注意力集中，为学生能顺利接受新知识创造有利条件 .